
第8章教学方案一弯曲应力和强度计算弯曲的概念和力学模型的简化基本内剪力和弯矩纯弯曲时的正应力横力弯曲时的正应力和强度计算容了解梁弯曲的工程实例。教学目2、熟练掌握画剪力图和弯矩图。3、掌握纯弯梁横截面上的正应力分布及计算。、熟练掌握弯曲强度计算。的重点梁横截面上的正应力计算及梁的强度计算。、难点
第 8 章 教学方案 ——弯曲应力和强度计算 基 本 内 容 弯曲的概念和力学模型的简化 剪力和弯矩 纯弯曲时的正应力 横力弯曲时的正应力和强度计算 教 学 目 的 1、了解梁弯曲的工程实例。 2、熟练掌握画剪力图和弯矩图。 3、掌握纯弯梁横截面上的正应力分布及计算。 4、熟练掌握弯曲强度计算。 重 点 、 难 点 梁横截面上的正应力计算及梁的强度计算
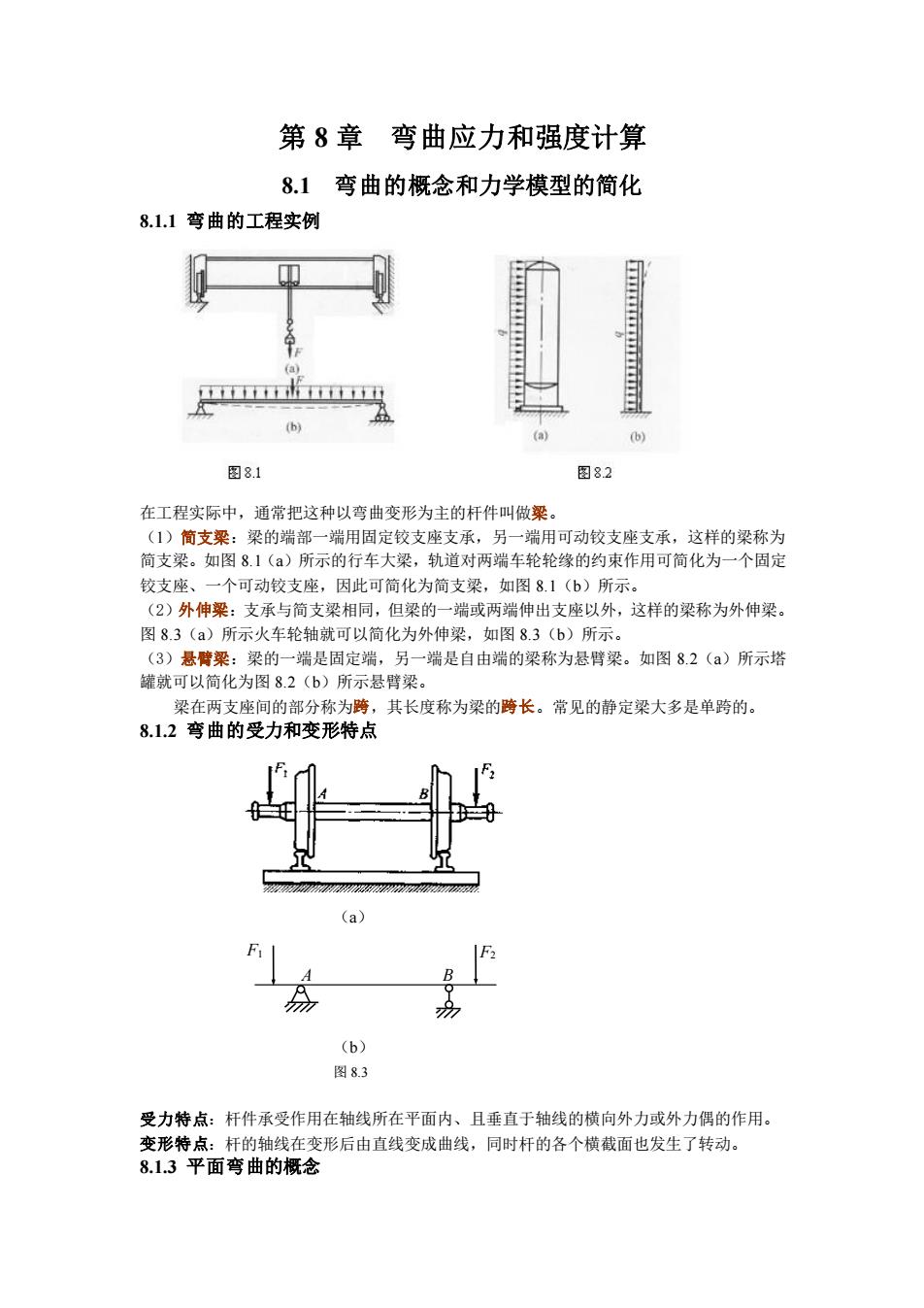
第8章弯曲应力和强度计算8.13弯曲的概念和力学模型的简化8.1.1 弯曲的工程实例T7T图8.1图8.2在工程实际中,通常把这种以弯曲变形为主的杆件叫做梁(1)简支梁:梁的端部一端用固定铰支座支承,另一端用可动铰支座支承,这样的梁称为简支梁。如图8.1(a)所示的行车大梁,轨道对两端车轮轮缘的约束作用可简化为一个固定铰支座、一个可动铰支座,因此可简化为简支梁,如图8.1(b)所示。(2)外伸梁:支承与简支梁相同,但梁的一端或两端伸出支座以外,这样的梁称为外伸梁图8.3(a)所示火车轮轴就可以简化为外伸梁,如图8.3(b)所示。(3)悬臂梁:梁的一端是固定端,另一端是自由端的梁称为悬臂梁。如图8.2(a)所示塔罐就可以简化为图8.2(b)所示悬臂梁。梁在两支座间的部分称为跨,其长度称为梁的跨长。常见的静定梁大多是单跨的。8.1.2弯曲的受力和变形特点1上1不(b图 8.3受力特点:杆件承受作用在轴线所在平面内、且垂直于轴线的横向外力或外力偶的作用。变形特点:杆的轴线在变形后由直线变成曲线,同时杆的各个横截面也发生了转动。8.1.3平面弯曲的概念
(a) (b) 图 8.3 F2 A F1 B 第 8 章 弯曲应力和强度计算 8.1 弯曲的概念和力学模型的简化 8.1.1 弯曲的工程实例 在工程实际中,通常把这种以弯曲变形为主的杆件叫做梁。 (1)简支梁:梁的端部一端用固定铰支座支承,另一端用可动铰支座支承,这样的梁称为 简支梁。如图 8.1(a)所示的行车大梁,轨道对两端车轮轮缘的约束作用可简化为一个固定 铰支座、一个可动铰支座,因此可简化为简支梁,如图 8.1(b)所示。 (2)外伸梁:支承与简支梁相同,但梁的一端或两端伸出支座以外,这样的梁称为外伸梁。 图 8.3(a)所示火车轮轴就可以简化为外伸梁,如图 8.3(b)所示。 (3)悬臂梁:梁的一端是固定端,另一端是自由端的梁称为悬臂梁。如图 8.2(a)所示塔 罐就可以简化为图 8.2(b)所示悬臂梁。 梁在两支座间的部分称为跨,其长度称为梁的跨长。常见的静定梁大多是单跨的。 8.1.2 弯曲的受力和变形特点 受力特点:杆件承受作用在轴线所在平面内、且垂直于轴线的横向外力或外力偶的作用。 变形特点:杆的轴线在变形后由直线变成曲线,同时杆的各个横截面也发生了转动。 8.1.3 平面弯曲的概念

如图:梁的横截面都有一根纵向对称轴。整个杆件有一个包含轴线在内的纵向对称面纵向对称对称轮梁变形后的轴线与外力在ALV同一平面内图8.4当外力(载荷与支座反力)都作用在该对称面内时,梁弯曲变形后,轴线仍保持在此对称平面内,成为一条平面曲线(图8.4),这种弯曲叫做对称弯曲。通常将梁变形后的轴线所在平面与外力所在平面相重合的弯曲变形称为平面弯曲。8.2剪力和弯矩8.2.1剪力和弯矩在弯曲外力作用下,梁产生弯曲变形,横截面上的内力可以通过截面法求出来如图8.5(a)所示的简支梁,在外力作用下处于平衡状态。现假想在距左端为x的m-m截面处,用一假想的垂直于梁轴线的平面将梁截为两段,取其中的任一段梁,例如取左段梁研究,并将右段梁对它的作用以截面上的内力来代替(图8.5(b)。为使左段梁保持平衡,在其右端截面上,应该有两个内力:沿截面切线方向的力F。和力偶矩M,力F。称为剪力,力偶矩M称为弯矩1.剪力和弯矩的计算X上述梁在截面m-m上内力一一剪力F。利弯矩M的具体数值可由平衡条件求得,即ZY=0, Fm-Fo=0FRalZMo=0,-Frux-M=0(矩心0Fa为截面m-m 的形心)图 8.5可得Fo=Fr,M=Feax。2.剪力、弯矩符号的规定为了研究方便,现对梁的内力一一剪力和弯矩作如下的正负号规定。(1)剪力符号规定取微段梁,若截面上的剪力对梁上任意一点的矩为顺时针转向时,剪力为正;反之为
如图:梁的横截面都有一根纵向对称轴。整个杆件有一个包含轴线在内的纵向对称面。 当外力(载荷与支座反力)都作用在该对称面内时,梁弯曲变形后,轴线仍保持在此对 称平面内,成为一条平面曲线(图 8.4),这种弯曲叫做对称弯曲。通常将梁变形后的轴线所 在平面与外力所在平面相重合的弯曲变形称为平面弯曲。 8.2 剪力和弯矩 8.2.1 剪力和弯矩 在弯曲外力作用下,梁产生弯曲变形,横截面上的内力可以通过截面法求出来。 如图 8.5(a)所示的简支梁,在外力作用下处于平衡状态。现假想在距左端为 x 的 m-m 截面处,用一假想的垂直于梁轴线的平面将梁截为两段,取其中的任一段梁,例如取左段梁 研究,并将右段梁对它的作用以截面上的内力来代替(图 8.5(b))。 为使左段梁保持平衡,在其右端截面上,应该有两个内力: 沿截面切线方向的力 FQ 和力偶矩 M ,力 FQ 称 为剪力,力偶矩 M 称为弯矩。 1.剪力和弯矩的计算 上述梁在截面 m-m 上内力——剪力 FQ 和 弯矩 M 的具体数值可由平衡条件求得,即 Y = 0, FRA − FQ = 0 MO = 0, − FRAx − M = 0 (矩心 O 为截面 m-m 的形心) 可得 FQ = FRA , M F x = RA 。 2.剪力、弯矩符号的规定 为了研究方便,现对梁的内力——剪力和弯矩作如下的正负号规定。 (1)剪力符号规定 取微段梁,若截面上的剪力对梁上任意一点的矩为顺时针转向时,剪力为正;反之为 梁变形后的轴线与外力在 同一平面内 A F1 F2 B 对称轴 纵向对称面 FB 图 8.4 图 8.5 FQ FQ

负。如图8.6所示。(2)弯矩符号规定取微段梁,若截面上的弯矩使得梁呈凹形时弯矩为正:使梁变成凸形时,弯矩为负。如图8.7所示。图8图8.6在计算横截面上的剪力和弯矩时,一般先按正向假设,这样通过列平衡方程计算出的结果,其符号就与规定的符号一致,不需要再进行符号讨论。8.2.2剪力方程和弯矩方程假设梁截面位置用沿梁轴线的坐标x表示,则梁的各个横截面上的剪力和弯矩都可以表示为坐标x的函数,即:Fo= Fo(x), M= M(x)通常把它们叫做梁的剪力方程和弯矩方程。8.2.3剪力图和弯矩图为了表明内力沿梁轴线的变化情况,通常用图形将剪力和弯矩沿梁长的变化情况表示出来,这样的图形分别称为剪力图和弯矩图。基本作法:先列出剪力方程和弯矩方程,建立以梁横截面位置×为横坐标,以横截面上的剪力和弯矩为纵坐标的坐标系,然后通过方程绘出表示Fc(g)或M(x)的图线。【例 8-1]图8.10(a)所示的简支梁,在全梁上受集度为9的均布载荷作用,试作梁的剪力图和弯矩图。解:求此梁的内力图时,应先求支座反力、列内力方程,最后由内力方程作内力图。Kx(1)求支座反力利用平衡方程求得A(a)Fra = Frn = l1o(2)建立内力方程取距左端为x的任意横截面,考虑截面左侧的梁段,则梁的剪力和弯矩方程分别为(b)lall(0<x<1)Fo(x)= FRA -qx =1g12/8qx1qxM(x)= Frax--qx(0≤x≤1)(c)(3)画内力图图8.10剪力方程是x的一次函数,所以剪力图是
负。如图 8.6 所示。 (2)弯矩符号规定 取微段梁,若截面上的弯矩使得梁呈凹形时,弯矩为正;使梁变成凸形时,弯矩为负。 如图 8.7 所示。 在计算横截面上的剪力和弯矩时,一般先按正向假设,这样通过列平衡方程计算出的结果, 其符号就与规定的符号一致,不需要再进行符号讨论。 8.2.2 剪力方程和弯矩方程 假设梁截面位置用沿梁轴线的坐标 x 表示,则梁的各个横截面上的剪力和弯矩都可以表 示为坐标 x 的函数,即: F F (x) Q = Q , M = M (x) 通常把它们叫做梁的剪力方程和弯矩方程。 8.2.3 剪力图和弯矩图 为了表明内力沿梁轴线的变化情况,通常用图形将剪力和弯矩沿梁长的变化情况表示出 来,这样的图形分别称为剪力图和弯矩图。 基本作法:先列出剪力方程和弯矩方程,建立以梁横截面位置 x 为横坐标,以横截面上 的剪力和弯矩为纵坐标的坐标系,然后通过方程绘出表示 F (x) Q 或 M (x) 的图线。 【例 8-1】 图 8.10(a)所示的简支梁,在全梁上受集度为 q 的均布载荷作用,试作 梁的剪力图和弯矩图。 解:求此梁的内力图时,应先求支座反力、 列内力方程,最后由内力方程作内力图。 (1)求支座反力 利用平衡方程求得 2 ql FRA = FRB = (2)建立内力方程 取距左端为 x 的任意横截面,考虑截面 左侧的梁段,则梁的剪力和弯矩方程分别为 qx ql F x F qx Q = RA − = − 2 ( ) (0< x < l ) 2 2 2 1 2 2 1 ( ) x qx ql M x F x qx = RA − = − (0≤ x ≤ l ) (3)画内力图 剪力方程是 x 的一次函数,所以剪力图是 FQ FQ FQ FQ 图 8.6 图 8.7 x x l A B x FA FB ql / 2 ql / 2 / 8 2 ql FQ M q (-) (+) (+) (a) (b) (c) 图 8.10

一条倾斜直线段。由F。(0)=,Fo()=-号可画出剪力图(图8.10(b)。弯矩方程是x的二次函数,所以弯矩图是一条二次抛物线。由M(O)=0M()=,M()=0可画出弯矩图(图8.10(c)。【例8.2】图8.11(a)所示的简支梁,在C点处受集中力F的作用,试作梁的剪力图和弯矩图。解:(1)求支座反力利用平衡方程求得FFRA=,FRB=(2)建立内力方程a由于梁在 C点处有集中力F的作用,0则在集中力两侧的梁段,其剪力和弯矩方程均不相同,因此,内力在全梁范围内不能用个统一的函数式来表达。必须以C为界,(-)将梁分为AC和 CB两段,分别写出其剪力Falt方程和弯矩方程。(b)对 AC 段梁,其剪力方程和弯矩方程分别为Fo(t)=Fb(0<x<a)M()=x (0≤x≤a)(c)对AC段梁,其剪力方程和弯矩方程分图8.11别为FaFo(x)=-(a<x<1)M(x)=Fr(I-x)-F(1-x) (asx≤I)(3)画内力图由两段梁的剪力方程可知,两段梁的剪力图各为一条平行于梁轴线的直线段。由两段梁的弯矩方程可知,两段梁的弯矩图各为一条斜直线段。绘出的剪力图和弯矩图如图8.11(b)、(c)所示。【例83】图8.12(a)所示的简支梁,在C点处受集中力偶M。的作用,试作梁的剪力图和弯矩图解:(1)求支座反力利用平衡方程求得MLFRB=FRA=
一条倾斜直线段。由 2 (0) ql FQ = , 2 ( ) ql F l Q = − 可画出剪力图(图 8.10(b))。 弯矩方 程是 x 的二 次函数 ,所 以弯 矩图是 一条 二次 抛物 线。由 M (0) = 0 , 8 ) 2 ( 2 l ql M = , M (l) = 0 可画出弯矩图(图 8.10(c))。 【例 8-2】 图 8.11(a)所示的简支梁,在 C 点处受集中力 F 的作用,试作梁的剪力图 和弯矩图。 解:(1)求支座反力 利用平衡方程求得 l Fb FRA = , l Fa FRB = (2)建立内力方程 由于梁在 C 点处有集中力 F 的作用, 则在集中力两侧的梁段,其剪力和弯矩方程 均不相同,因此,内力在全梁范围内不能用 一个统一的函数式来表达。必须以 C 为界, 将梁分为 AC 和 CB 两段,分别写出其剪力 方程和弯矩方程。 对 AC 段梁,其剪力方程和弯矩方程分 别为 l Fb FQ (x) = (0 x a) x l Fb M(x) = (0 x a) 对 AC 段梁,其剪力方程和弯矩方程分 别为 l Fa FQ (x) = − (a x l) ( ) ( ) (l x) l Fa M x F l x = B − = − (a x l) (3)画内力图 由两段梁的剪力方程可知,两段梁的剪力图各为一条平行于梁轴线的直线段。由两段梁 的弯矩方程可知,两段梁的弯矩图各为一条斜直线段。绘出的剪力图和弯矩图如图 8.11(b)、 (c)所示。 【例 8-3】图 8.12(a)所示的简支梁,在 C 点处受集中力偶 Me 的作用,试作梁的剪力 图和弯矩图。 解:(1)求支座反力 利用平衡方程求得 l M F e RA = − , l M F e RB = x B F a b C l A x Fab/l (+) Fb/l Fa /l (+) (-) FQ M x (a) (b) (c) 图 8.11