
式中,α为横截面上的正应力,F为横截面上的轴力,A为横截面面积根据轴力的正负号,当轴力为拉力时,正应力为拉应力,也是正的;当轴力为压力时,正应力为压应力,也是负的。【例6-3】起吊三角架如图6.7(a)所示,已知AB杆由2根截面面积为10.86cm2的角钢制成,F=130kN,α=30°。求杆AB横截面上的应力。聚贵(b)(a)图6.7解:(1)计算AB杆内力。取支点A为研究对象如图6.7(b),由平衡条件Y=0,得FNAB = 2F = 260kN(拉力)(2)计算CAB°260×103FNAB10.86X10×10~=119.7MPaCAB =6.3 材料拉伸和压缩时的力学性能材料的力学性能是指材料在外力作用下所呈现的有关强度和变形方面的特性。研究材料的力学性能的目的是确定材料在变形和破坏情况下的一些力学性能指标,作为选用材料计算材料强度、刚度的依据。材料的力学性能通过实验方法确定。6.3.1材料拉伸时的力学性能.拉伸试验常温静载下的拉伸试验是研究材料力学性能的常用基本试验。国家标准规定的金属材料标准圆试件如图6.8(a)所示。在试件中间等直部分取一段长度为1的测量长度,称为标距。标距和直径d有两种比例I=5d或/=10d,而对矩形截面,标距/与横截面面积A的比例为/=11.3VA或1=5.65/A,如图6.8(b)所示
式中, 为横截面上的正应力, FN 为横截面上的轴力, A 为横截面面积。 根据轴力的正负号,当轴力为拉力时,正应力为拉应力,也是正的;当轴力为压力时, 正应力为压应力,也是负的。 【例 6-3】 起吊三角架如图 6.7(a)所示,已知 AB 杆由 2 根截面面积为 10.86 2 cm 的角钢 制成, F =130kN, = 30 。求杆 AB 横截面上的应力。 图 6.7 解:(1)计算 AB 杆内力。取支点 A 为研究对象如图 6.7(b),由平衡条件 Y = 0 ,得 FNAB = 2F = 260kN (拉力) (2)计算 AB 。 10 119.7MPa 10.86 2 10 260 10 6 4 3 NAB AB = = = − − A F 6.3 材料拉伸和压缩时的力学性能 材料的力学性能是指材料在外力作用下所呈现的有关强度和变形方面的特性。研究材 料的力学性能的目的是确定材料在变形和破坏情况下的一些力学性能指标,作为选用材料, 计算材料强度、刚度的依据。材料的力学性能通过实验方法确定。 6.3.1 材料拉伸时的力学性能 ●.拉伸试验 常温静载下的拉伸试验是研究材料力学性能的常用基本试验。国家标准规定的金属材 料标准圆试件如图 6.8(a)所示。在试件中间等直部分取一段长度为 l 的测量长度,称为标 距。标距 l 和直径 d 有两种比例 l = 5d 或 l =10d ,而对矩形截面,标距 l 与横截面面积 A 的 比例为 l =11.3 A 或 l = 5.65 A ,如图 6.8(b)所示。 (a) (b)

14图6.8将拉伸试样装夹在试验机上,开动机器,使试件受到从零开始缓慢渐增的拉力F,是在试件标距1内产生相应的变形N,把试验过程中的拉力F与对应的变形N 绘制成F一△/曲线,称为拉伸图。拉伸图与试样的尺寸有关,为了消除试样尺寸的影响,把拉力F除以试样的横截面的原面积A,得出正应力,同时,把伸长量N/除以标距的原始长度1,得到应变6。以为纵坐标,为横坐标,作出表示与的关系图,称为应力一应变图或g-s图●低碳钢在拉伸时的力学性能低碳钢是工程上广泛使用的材料,其力学性质具有典型性。图6.9所示为低碳钢拉伸时的-8曲线。低碳钢的α-曲线可分为下列几个阶段(1)弹性阶段(ob段)在开始拉伸直至a点阶段,应力与应变:是成正比的。其极限位置α点对应的应力值称为比例极限,记为のp。它是应力与应变成正比的最大值。在这一阶段,应力与应变的关系可写成等式:图 6.9G=E-82该式称为拉压胡克定律。式中,E为与材料有关的比例常数,称为弹性模量。在应力一应变曲线上,当应力继续增加到b点时,曲线不再是直线,而呈微弯。在应力小于b点的应力值时,其变形是可以恢复的,即应力解除之后应变随之消失,这种变形称为弹性变形。b点对应的应力α。是发生弹性变形的极限值,称为弹性极限,它是材料只产生弹性变形的最大应力。由于一般材料的α、6两点相当接近,工程中对比例极限和弹性极限并不严格区分。(2)屈服阶段(bc'段)当应力超过弹性极限后,α一6曲线上出现一段接近水平线的微小波动线段,变形显著增长而应力几乎不变,材料暂时失去抵抗变形的能力,这种现象称为屈服(或流动)。在α-8曲线上c点所对应的应力值是届服阶段的最小值称为屈服极限,记为。,是衡量材料强度的重要指标。在这一阶段,材料主要产生塑性变形,所谓塑性变形是指载荷(应力)卸去后不能消
图 6.8 将拉伸试样装夹在试验机上,开动机器,使试件受到从零开始缓慢渐增的拉力 F ,于 是在试件标距 l 内产生相应的变形 l ,把试验过程中的拉力 F 与对应的变形 l 绘制成 F − l 曲线,称为拉伸图。拉伸图与试样的尺寸有关,为了消除试样尺寸的影响,把拉力 F 除以试样的横截面的原面积 A ,得出正应力 ,同时,把伸长量 l 除以标距的原始长度 l , 得到应变 。以 为纵坐标, 为横坐标,作出表示 与 的关系图,称为应力—应变图 或 − 图。 ●低碳钢在拉伸时的力学性能 低碳钢是工程上广泛使用的材料,其力学性质具有典型性。图 6.9 所示为低碳钢拉伸时 的 − 曲线。 低碳钢的 − 曲线可分为下列几个阶段。 (1)弹性阶段( ob 段) 在开始拉伸直至 a 点阶段,应力 与应变 是成正比的。其极限位置 a 点对应的应力值称为 比例极限,记为 P 。它是应力与应变成正比的 最大值。在这一阶段,应力与应变的关系可写成 等式: = E (6-2) 该式称为拉压胡克定律。式中, E 为与材料有关的比例常数,称为弹性模量。 在应力—应变曲线上,当应力继续增加到 b 点时,曲线不再是直线,而呈微弯。在应力 小于 b 点的应力值时,其变形是可以恢复的,即应力解除之后应变随之消失,这种变形称为 弹性变形。b 点对应的应力 e 是发生弹性变形的极限值,称为弹性极限,它是材料只产生 弹性变形的最大应力。由于一般材料的 a、b 两点相当接近,工程中对比例极限和弹性极限 并不严格区分。 (2) 屈服阶段( / bc 段) 当应力超过弹性极限后, − 曲线上出现一段接近水平线的微小波动线段,变形显著 增长而应力几乎不变,材料暂时失去抵抗变形的能力,这种现象称为屈服(或流动)。在 − 曲线上 c 点所对应的应力值是屈服阶段的最小值称为屈服极限,记为 s 。 s 是衡量材料强 度的重要指标。 在这一阶段,材料主要产生塑性变形,所谓塑性变形是指载荷(应力)卸去后不能消 图 6.9

失的变形,又称残余变形。对于表面光滑的试件,在屈服时会由于金属材料内部晶格之间产生相对滑动而在其表面上出现许多与轴线大致成45°的条纹,这些条纹称为滑移线。如图6.10所示。图6.10图 611(3)强化阶段(c'd段)过了屈服阶段后,材料又恢复了抵抗变形的能力,要使它继续变形必须增加拉力。这种现象称为材料的强化。强化阶段的最高点d所对应的应力值是材料所能承受的最大应力,称为强度极限。记为。表示材料所能承受的最大应力,也是衡量材料强度的重要指标。强化阶段的变形大部分也是塑性变形,同时试件的横向尺寸明显缩小。(4)局部变形阶段(de段应力达到强度极限后,在试件某一局部区域内,截面横向尺寸急剧缩小,形成颈缩现象(图6.11)。由于颈缩部分的横截面面积迅速减少,使试件继续伸长所需要的拉力也相应减少。最后试件在颈缩处被拉断。试件被拉断后,弹性变形消失,塑性变形被保留了下来。常用下述两个指标来度量材料的塑性性能。设试样拉断后的标距长度为1,原始长度为1,则定义×100%(6-3)为材料的延伸率或伸长率。设试样的原始横截面面积为A,拉断后颈缩处的最小截面面积为A,则定义A-A×100%(6-4)为材料的断面收缩率。材料的延伸率和断面收缩率越大,说明材料塑性越好。工程上通常按延伸率的大小把材料分为两类:8≥5%为塑性材料:8≤5%为脆性材料。对于低碳钢,其塑性指标约为:8=20%~30%,Φ=60%。(5)卸载定律与冷作硬化如在强化阶段的某点「处给试样缓慢卸载,则应力与应变沿直线fo,变化,且斜直线fo,大致与oa平行(图6-8)。上述规律称为卸载定律。拉力完全卸除后,0,02代表消失了的弹性应变,而00,表示不能消失的塑性应变
失的变形,又称残余变形。对于表面光滑的试件,在屈服时会由于金属材料内部晶格之间产 生相对滑动而在其表面上出现许多与轴线大致成 45 的条纹,这些条纹称为滑移线。如图 6.10 所示。 (3) 强化阶段( c d / 段) 过了屈服阶段后,材料又恢复了抵抗变形的能力,要使它继续变形必须增加拉力。这 种现象称为材料的强化。强化阶段的最高点 d 所对应的应力值是材料所能承受的最大应力, 称为强度极限。记为 b 。 b 表示材料所能承受的最大应力,也是衡量材料强度的重要指标。 强化阶段的变形大部分也是塑性变形,同时试件的横向尺寸明显缩小。 (4) 局部变形阶段( de 段) 应力达到强度极限后,在试件某一局部区域内,截面横向尺寸急剧缩小,形成颈缩现 象(图 6.11)。由于颈缩部分的横截面面积迅速减少,使试件继续伸长所需要的拉力也相应 减少。最后试件在颈缩处被拉断。 试件被拉断后,弹性变形消失,塑性变形被保留了下来。常用下述两个指标来度量材 料的塑性性能。 设试样拉断后的标距长度为 1 l ,原始长度为 l ,则定义 − = l l l 1 100% (6-3) 为材料的延伸率或伸长率。 设试样的原始横截面面积为 A ,拉断后颈缩处的最小截面面积为 A 1,则定义 − = A A A1 100% (6-4) 为材料的断面收缩率。 材料的延伸率和断面收缩率越大,说明材料塑性越好。工程上通常按延伸率的大小把 材料分为两类: 5%为塑性材料; 5%为脆性材料。对于低碳钢,其塑性指标约为: = 20%~30%, = 60%。 (5) 卸载定律与冷作硬化 如在强化阶段的某点 f 处给试样缓慢卸载,则应力与应变沿直线 1 fo 变化,且斜直线 1 fo 大致与 oa 平行(图 6-8)。上述规律称为卸载定律。拉力完全卸除后, o1o2 代表消失了 的弹性应变,而 1 oo 表示不能消失的塑性应变。 图 6.10 图 6.11
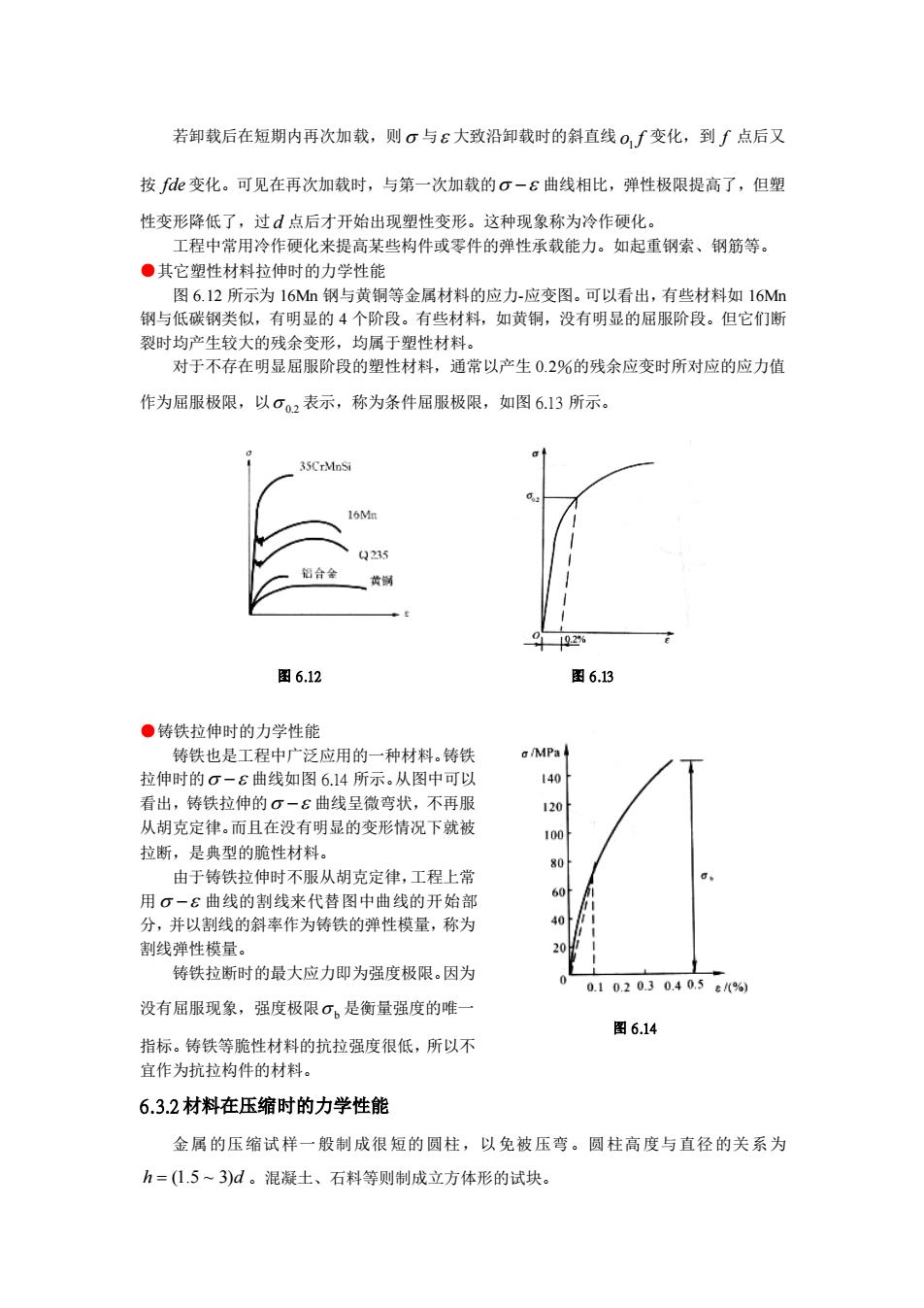
若卸载后在短期内再次加载,则与ε大致沿卸载时的斜直线o,f变化,到,点后又按fde变化。可见在再次加载时,与第一次加载的α一6曲线相比,弹性极限提高了,但塑性变形降低了,过d点后才开始出现塑性变形。这种现象称为冷作硬化。工程中常用冷作硬化来提高某些构件或零件的弹性承载能力。如起重钢索、钢筋等。●其它塑性材料拉伸时的力学性能图6.12所示为16Mn钢与黄铜等金属材料的应力-应变图。可以看出,有些材料如16Mn钢与低碳钢类似,有明显的4个阶段。有些材料,如黄铜,没有明显的屈服阶段。但它们断裂时均产生较大的残余变形,均属于塑性材料。对于不存在明显屈服阶段的塑性材料,通常以产生0.2%的残余应变时所对应的应力值作为屈服极限,以00.2表示,称为条件屈服极限,如图6.13所示。图 6.13图 6.12 铸铁拉伸时的力学性能铸铁也是工程中广泛应用的一种材料。铸铁fMra拉伸时的-曲线如图6.14所示。从图中可以140F看出,铸铁拉伸的-曲线呈微弯状,不再服120从胡克定律。而且在没有明显的变形情况下就被100拉断,是典型的脆性材料。g0由于铸铁拉伸时不服从胡克定律,工程上常用α-曲线的割线来代替图中曲线的开始部分,并以割线的斜率作为铸铁的弹性模量,称为割线弹性模量铸铁拉断时的最大应力即为强度极限。因头0.10.20.30.40.5/%)没有屈服现象,强度极限,是衡量强度的唯图6.14指标。铸铁等脆性材料的抗拉强度很低,所以不宜作为抗拉构件的材料。6.3.2材料在压缩时的力学性能金属的压缩试样一般制成很短的圆柱,以免被压弯。圆柱高度与直径的关系为h=(1.5~3)d。混凝土、石料等则制成立方体形的试块
若卸载后在短期内再次加载,则 与 大致沿卸载时的斜直线 o f 1 变化,到 f 点后又 按 fde 变化。可见在再次加载时,与第一次加载的 − 曲线相比,弹性极限提高了,但塑 性变形降低了,过 d 点后才开始出现塑性变形。这种现象称为冷作硬化。 工程中常用冷作硬化来提高某些构件或零件的弹性承载能力。如起重钢索、钢筋等。 ●其它塑性材料拉伸时的力学性能 图 6.12 所示为 16Mn 钢与黄铜等金属材料的应力-应变图。可以看出,有些材料如 16Mn 钢与低碳钢类似,有明显的 4 个阶段。有些材料,如黄铜,没有明显的屈服阶段。但它们断 裂时均产生较大的残余变形,均属于塑性材料。 对于不存在明显屈服阶段的塑性材料,通常以产生 0.2%的残余应变时所对应的应力值 作为屈服极限,以 0.2 表示,称为条件屈服极限,如图 6.13 所示。 ●铸铁拉伸时的力学性能 铸铁也是工程中广泛应用的一种材料。铸铁 拉伸时的 − 曲线如图 6.14 所示。从图中可以 看出,铸铁拉伸的 − 曲线呈微弯状,不再服 从胡克定律。而且在没有明显的变形情况下就被 拉断,是典型的脆性材料。 由于铸铁拉伸时不服从胡克定律,工程上常 用 − 曲线的割线来代替图中曲线的开始部 分,并以割线的斜率作为铸铁的弹性模量,称为 割线弹性模量。 铸铁拉断时的最大应力即为强度极限。因为 没有屈服现象,强度极限 b 是衡量强度的唯一 指标。铸铁等脆性材料的抗拉强度很低,所以不 宜作为抗拉构件的材料。 6.3.2 材料在压缩时的力学性能 金属的压缩试样一般制成很短的圆柱,以免被压弯。圆柱高度与直径的关系为 h = (1.5 ~ 3)d 。混凝土、石料等则制成立方体形的试块。 图 6.12 图 6.13 图 6.14