
第10章教学方案-应力状态和强度理论应力状态概述二向应力状态分析的解析法基本内容三向应力状态强度理论概述四种常用的强度理论强度理论的应用了解应力状态分析的原因和一点应力状态的概念,掌握用微元描述一点应力状态。2、掌握平面应力状态中斜面上的正应力、切应力计算,熟练掌握教学目的主应力、主方向的确定及最大切应力的计算。了解广义胡克定律。了解强度理论的概念。5、掌握四种常用的强度理论,了解四种强度理论应用条件。重点一点应力状态的概念及描述;强度理论的概念及应用。难点
第 10 章 教学方案 ——应力状态和强度理论 基 本 内 容 应力状态概述 二向应力状态分析的解析法 三向应力状态 强度理论概述 四种常用的强度理论 强度理论的应用 教 学 目 的 1、了解应力状态分析的原因和一点应力状态的概念,掌握用微元 描述一点应力状态。 2、掌握平面应力状态中斜面上的正应力、切应力计算,熟练掌握 主应力、主方向的确定及最大切应力的计算。 3、了解广义胡克定律。 4、了解强度理论的概念。 5、掌握四种常用的强度理论 6、了解四种强度理论应用条件。 重 点 、 难 点 一点应力状态的概念及描述;强度理论的概念及应用

第10章应力状态和强度理论10.1应力状态概述10.1.1问题的提出工程中有许多构件,其危险截面上的危险点同时承受正应力和切应力,这种受力状态称为复杂应力状态。由于复杂应力状态变化繁多,在强度计算时不可能一二一通过实验确定失效时的极限应力。因此必须研究复杂应力状态的应力在各个方向的变化规律,为失效原因分析提供基础。10.1.2应力状态的概念受力构件内某一点处,各个不同方位截面上的应力及其关系称为一点的应力状态。为了研究一点的应力状态,可围绕该点取单元体。因为单元体的尺寸非常微小,可以认为各个面上的应力均匀分布相对的两个面上的应力情况完全相同。构件上一点的应力状态,可由围绕该点的单元体各面上的应力情况表示。换句话说,单元体的受力就代表该点的应力状态。10.1.3单元体的取法通常用应力已知的截面来截取单元体。例如在图10.1(a)所示的轴向拉伸构件中,为了分析 A点的应力状态,围绕A点用横截面和纵向截面截取出单元体研究,A点单元体受力如图所示。在图10.(b)所示的扭转圆轴中,为了分析表面上C点的应力状态,围绕C点用左右两个横截面、上下两个纵向截面和平行表面的一个纵向截面截取出单元体研究,C点单元体受力如图所示。在图10.1(c)所示的矩形截面悬臂梁上,若研究m-m截面上A、B、C三点的应力状态,围绕三点分别用横截面利纵向截面截取出单元体研究。横截面上的应力分布如图,大小可由弯曲应力计算公式确定。A点在梁横截面的最上端,横截面方向只受正应力作用,其单元体受力如图示:B点在中性轴上,横截面上只受切应力作用,根据该截面上剪力的方向,可确定切应力的方向如图,其单元体受力如图示:同理可确定C点的单元体受力如图示
第 10 章 应力状态和强度理论 10.1 应力状态概述 10.1.1 问题的提出 工程中有许多构件,其危险截面上的危险点同时承受正应力和切应力,这种受力状态称为复杂 应力状态。由于复杂应力状态变化繁多,在强度计算时不可能一一通过实验确定失效时的极限应力。 因此必须研究复杂应力状态的应力在各个方向的变化规律,为失效原因分析提供基础。 10.1.2 应力状态的概念 受力构件内某一点处,各个不同方位截面上的应力及其关系称为一点的应力状态。为了研究一点 的应力状态,可围绕该点取单元体。因为单元体的尺寸非常微小,可以认为各个面上的应力均匀分布, 相对的两个面上的应力情况完全相同。构件上一点的应力状态,可由围绕该点的单元体各面上的应力 情况表示。换句话说,单元体的受力就代表该点的应力状态。 10.1.3 单元体的取法 通常用应力已知的截面来截取单元体。例如在图 10.1(a)所示的轴向拉伸构件中,为了分析 A 点的应力状态,围绕 A 点用横截面和纵向截面截取出单元体研究,A 点单元体受力如图所示。在图 10.1 (b)所示的扭转圆轴中,为了分析表面上 C 点的应力状态,围绕 C 点用左右两个横截面、上下两个 纵向截面和平行表面的一个纵向截面截取出单元体研究,C 点单元体受力如图所示。在图 10.1(c) 所示的矩形截面悬臂梁上,若研究 m-m 截面上 A、B、C 三点的应力状态,围绕三点分别用横截面和 纵向截面截取出单元体研究。横截面上的应力分布如图,大小可由弯曲应力计算公式确定。A 点在梁 横截面的最上端,横截面方向只受正应力作用,其单元体受力如图示;B 点在中性轴上,横截面上只 受切应力作用,根据该截面上剪力的方向,可确定切应力的方向如图,其单元体受力如图示;同理可 确定 C 点的单元体受力如图示
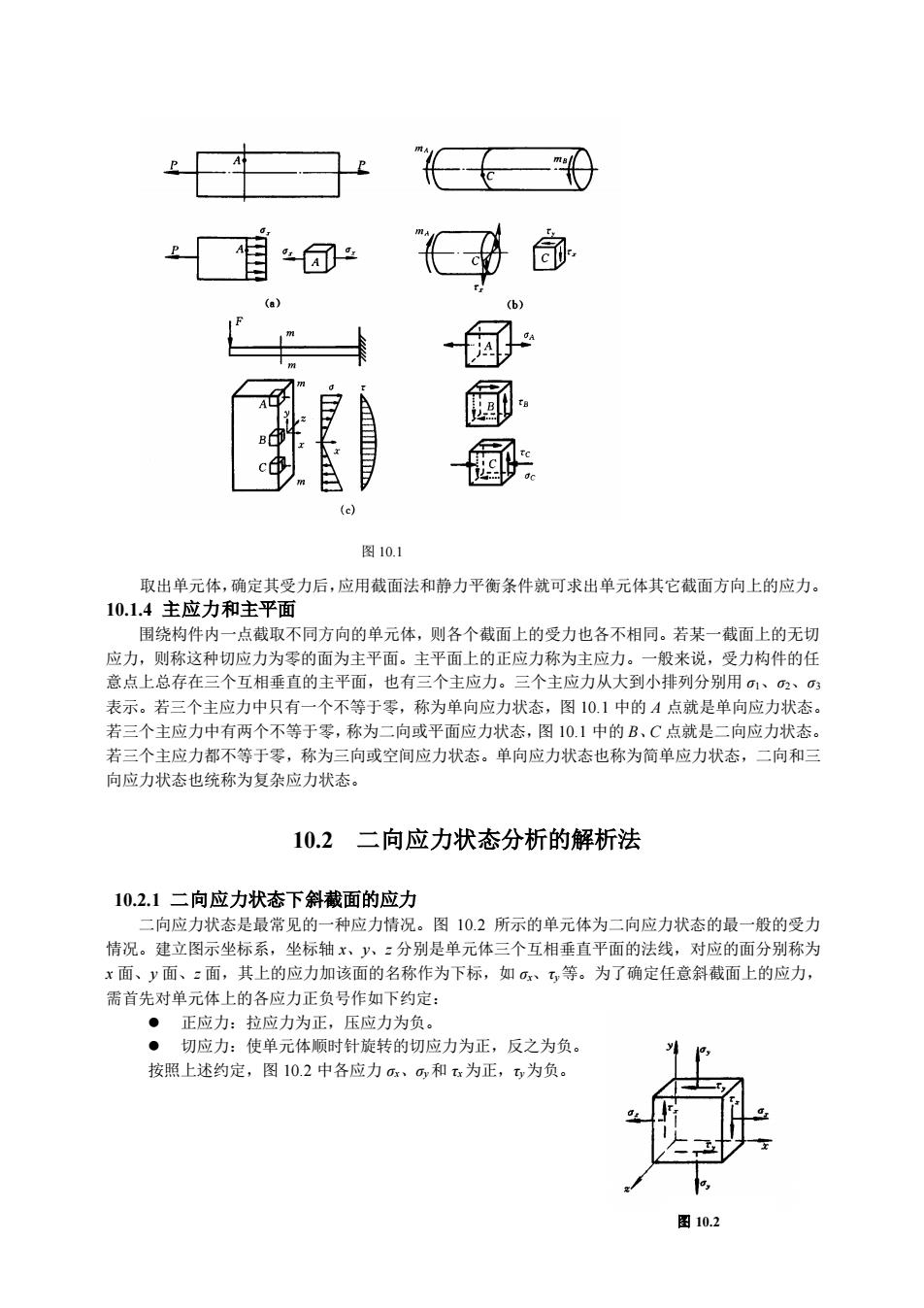
0存司+H(a)自皇c中日图10.1取出单元体,确定其受力后,应用截面法和静力平衡条件就可求出单元体其它截面方向上的应力10.1.4主应力和主平面用绕构件内一点载取不同方向的单元体,则各个载面上的受力也各不相同。若某一截面上的无切应力,则称这种切应力为零的面为主平面。主平面上的正应力称为主应力。一般来说,受力构件的任意点上总存在三个互相垂直的主平面,也有三个主应力。三个主应力从大到小排列分别用01、02、03表示。若三个主应力中只有一个不等于零,称为单向应力状态,图10.1中的A点就是单向应力状态。若三个主应力中有两个不等于零,称为二向或平面应力状态,图10.1中的B、C点就是二向应力状态。若三个主应力都不等于零,称为三向或空间应力状态。单向应力状态也称为简单应力状态,二向和三向应力状态也统称为复杂应力状态10.2二向应力状态分析的解析法10.2.1二向应力状态下斜截面的应力向应力状态是最常见的一种应力情况。图10.2所示的单元体为二向应力状态的最一般的受力情况。建立图示坐标系,坐标轴、六、=分别是单元体三个互相垂直平面的法线,对应的面分别称为x面、y面、面,其上的应力加该面的名称作为下标,如o、,等。为了确定任意斜截面上的应力,需首先对单元体上的各应力正负号作如下约定:正应力:拉应力为正,压应力为负。切应力:使单元体顺时针旋转的切应力为正,反之为负。按照上述约定,图10.2中各应力6x、6和为正,ty为负。图10.2
取出单元体,确定其受力后,应用截面法和静力平衡条件就可求出单元体其它截面方向上的应力。 10.1.4 主应力和主平面 围绕构件内一点截取不同方向的单元体,则各个截面上的受力也各不相同。若某一截面上的无切 应力,则称这种切应力为零的面为主平面。主平面上的正应力称为主应力。一般来说,受力构件的任 意点上总存在三个互相垂直的主平面,也有三个主应力。三个主应力从大到小排列分别用 σ1、σ2、σ3 表示。若三个主应力中只有一个不等于零,称为单向应力状态,图 10.1 中的 A 点就是单向应力状态。 若三个主应力中有两个不等于零,称为二向或平面应力状态,图 10.1 中的 B、C 点就是二向应力状态。 若三个主应力都不等于零,称为三向或空间应力状态。单向应力状态也称为简单应力状态,二向和三 向应力状态也统称为复杂应力状态。 10.2 二向应力状态分析的解析法 10.2.1 二向应力状态下斜截面的应力 二向应力状态是最常见的一种应力情况。图 10.2 所示的单元体为二向应力状态的最一般的受力 情况。建立图示坐标系,坐标轴 x、y、z 分别是单元体三个互相垂直平面的法线,对应的面分别称为 x 面、y 面、z 面,其上的应力加该面的名称作为下标,如 σx、τy等。为了确定任意斜截面上的应力, 需首先对单元体上的各应力正负号作如下约定: ⚫ 正应力:拉应力为正,压应力为负。 ⚫ 切应力:使单元体顺时针旋转的切应力为正,反之为负。 按照上述约定,图 10.2 中各应力 σx、σy和 τx为正,τy为负。 图 10.1 图 10.2
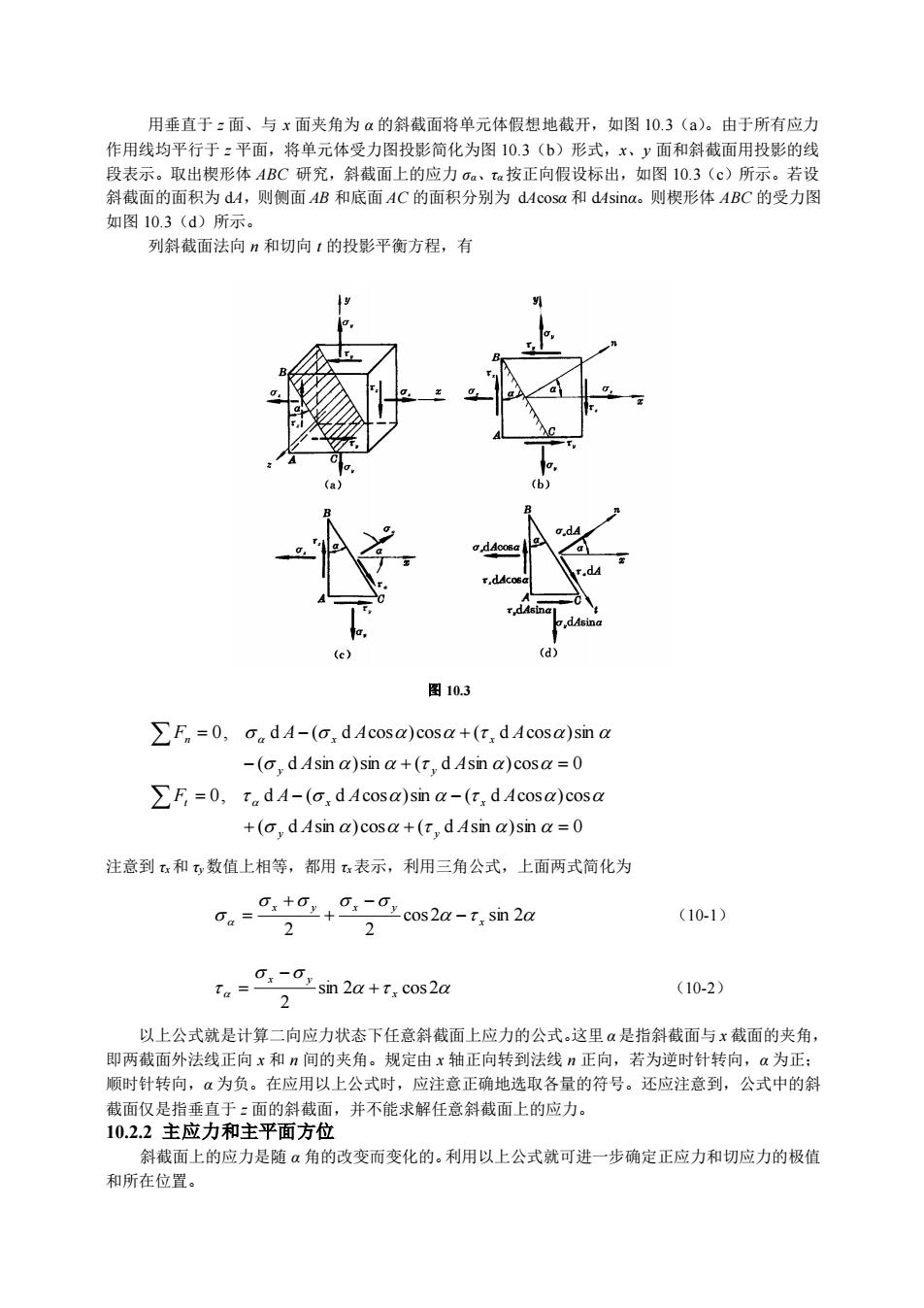
用垂直于=面、与x面夹角为α的斜截面将单元体假想地截开,如图10.3(a)。由于所有应力作用线均平行于,平面,将单元体受力图投影简化为图10.3(b)形式,x、y面和斜截面用投影的线段表示。取出楔形体 ABC 研究,斜截面上的应力 ca、ta按正向假设标出,如图 10.3(c)所示。若设斜截面的面积为dA,则侧面 AB和底面AC 的面积分别为dAcosα 和dAsinα。则楔形体ABC 的受力图如图10.3(d)所示。列斜截面法向n和切向t的投影平衡方程,有图10.3ZF,=0, a dA-(o, dAcosa)cosα+(t, dAcosa)sin α-(c, d Asin α)sin α+(t, d Asin α)cosα= CZF, =0, tadA-(o, dAcosa)sin α-(t, dAcosa)cosα+(c, d Asin a)sα+(t,dAsin α)sin 注意到和,数值上相等,都用表示,利用三角公式,上面两式简化为a,+a,0-0cin20(10-1)(10-2)2α+t,cos2a以上公式就是计算二向应力状态下任意斜截面上应力的公式。这里α是指斜截面与×截面的夹角,即两截面外法线正向 x和 n 间的夹角。规定由x 轴正向转到法线n 正向,若为逆时针转向,α为正顺时针转向,α为负。在应用以上公式时,应注意正确地选取各量的符号。还应注意到,公式中的斜截面仅是指垂直于:面的斜截面,并不能求解任意斜截面上的应力。10.2.2主应力和主平面方位斜截面上的应力是随α角的改变而变化的。利用以上公式就可进一步确定正应力和切应力的极值和所在位置
用垂直于 z 面、与 x 面夹角为 α 的斜截面将单元体假想地截开,如图 10.3(a)。由于所有应力 作用线均平行于 z 平面,将单元体受力图投影简化为图 10.3(b)形式,x、y 面和斜截面用投影的线 段表示。取出楔形体 ABC 研究,斜截面上的应力 σα、τα按正向假设标出,如图 10.3(c)所示。若设 斜截面的面积为 dA,则侧面 AB 和底面 AC 的面积分别为 dAcosα 和 dAsinα。则楔形体 ABC 的受力图 如图 10.3(d)所示。 列斜截面法向 n 和切向 t 的投影平衡方程,有 ( d sin ) cos ( d sin )sin 0 0, d ( d cos )sin ( d cos ) cos ( d sin )sin ( d sin ) cos 0 0, d ( d cos ) cos ( d cos )sin + + = = − − − + = = − + A A F A A A A A F A A A y y t x x y y n x x 注意到 τx和 τy数值上相等,都用 τx表示,利用三角公式,上面两式简化为 cos 2 sin 2 2 2 x x y x y − − + + = (10-1) sin 2 cos 2 2 x x y + − = (10-2) 以上公式就是计算二向应力状态下任意斜截面上应力的公式。这里 α 是指斜截面与 x 截面的夹角, 即两截面外法线正向 x 和 n 间的夹角。规定由 x 轴正向转到法线 n 正向,若为逆时针转向,α 为正; 顺时针转向,α 为负。在应用以上公式时,应注意正确地选取各量的符号。还应注意到,公式中的斜 截面仅是指垂直于 z 面的斜截面,并不能求解任意斜截面上的应力。 10.2.2 主应力和主平面方位 斜截面上的应力是随 α 角的改变而变化的。利用以上公式就可进一步确定正应力和切应力的极值 和所在位置。 图 10.3
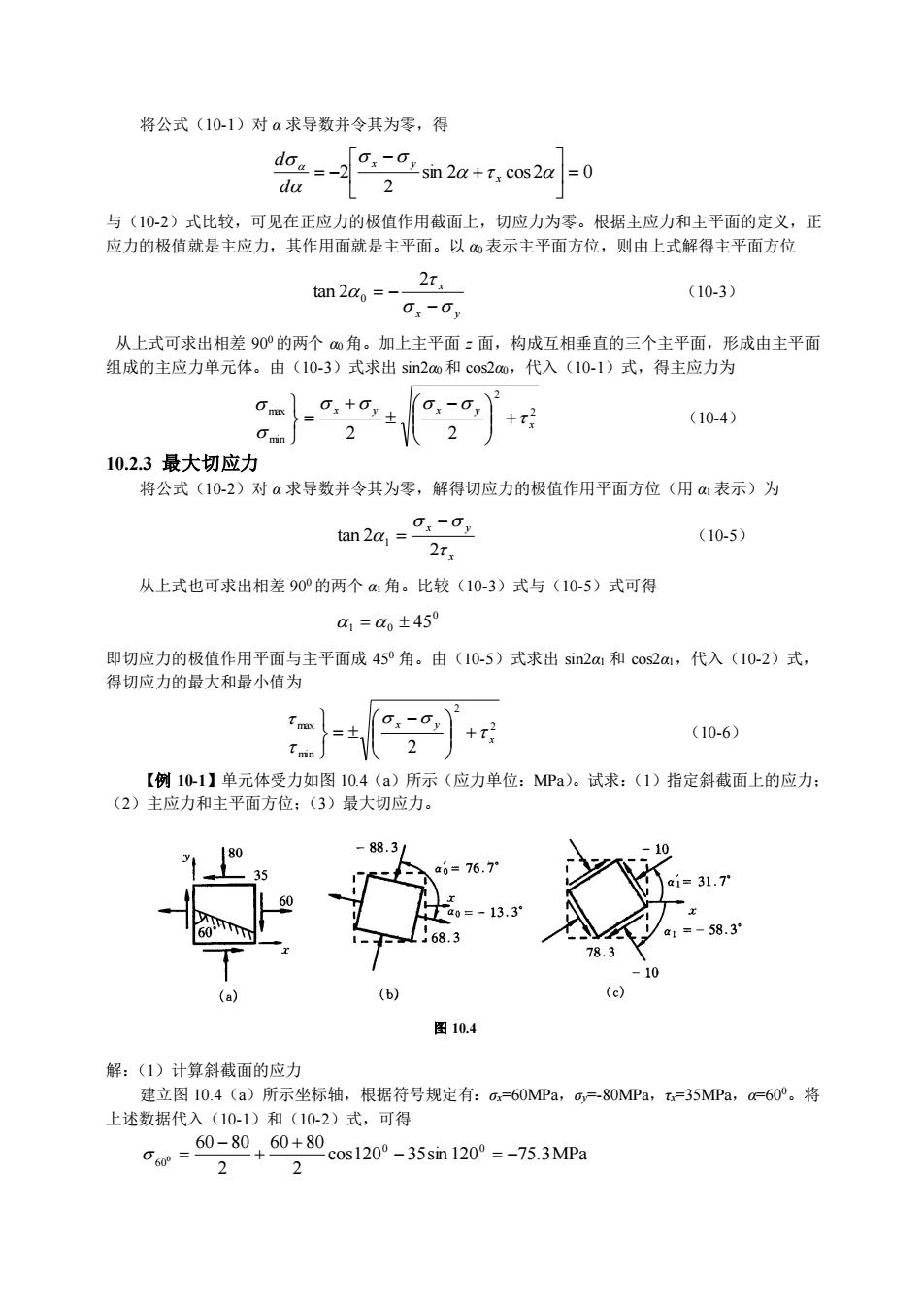
将公式(10-1)对α求导数并令其为零,得o-doa=sin 2α+T, cos2α|-=0da2与(10-2)式比较,可见在正应力的极值作用截面上,切应力为零。根据主应力和主平面的定义,正应力的极值就是主应力,其作用面就是主平面。以表示主平面方位,则由上式解得主平面方位2ttan 2αg =(10-3)0-0从上式可求出相差90°的两个角。加上主平面:面,构成互相垂直的三个主平面,形成由主平面组成的主应力单元体。由(10-3)式求出 sin2ao和cos2ao,代入(10-1)式,得主应力为o.-0. +:Om/o,+o,+(10-4)amia10.2.3最大切应力将公式(10-2)对α求导数并令其为零,解得切应力的极值作用平面方位(用α表示)为0.-0tan 2α,(10-5)2T从上式也可求出相差90°的两个αi角。比较(10-3)式与(10-5)式可得αj=αg± 450即切应力的极值作用平面与主平面成45°角。由(10-5)式求出sin2αi和cos2αi,代入(10-2)式,得切应力的最大和最小值为(10-6)=+TminJ【例10-1】单元体受力如图10.4(a)所示(应力单位:MPa)。试求:(1)指定斜截面上的应力;(2)主应力和主平面方位:(3)最大切应力(a)(b)图10.4解:(1)计算斜截面的应力建立图10.4(a)所示坐标轴,根据符号规定有:0f=60=600将上述数据代入(10-1)和(10-2)式,可得_60-80,60±80cos120 35sin 120° =-75.3MPa0.600L
将公式(10-1)对 α 求导数并令其为零,得 sin 2 cos 2 0 2 2 = + − = − x x y d d 与(10-2)式比较,可见在正应力的极值作用截面上,切应力为零。根据主应力和主平面的定义,正 应力的极值就是主应力,其作用面就是主平面。以 α0 表示主平面方位,则由上式解得主平面方位 x y x − = − 2 tan 2 0 (10-3) 从上式可求出相差 900 的两个 α0 角。加上主平面 z 面,构成互相垂直的三个主平面,形成由主平面 组成的主应力单元体。由(10-3)式求出 sin2α0 和 cos2α0,代入(10-1)式,得主应力为 2 2 min max 2 2 x x y x y + − + = (10-4) 10.2.3 最大切应力 将公式(10-2)对 α 求导数并令其为零,解得切应力的极值作用平面方位(用 α1 表示)为 x x y 2 tan 2 1 − = (10-5) 从上式也可求出相差 900 的两个 α1 角。比较(10-3)式与(10-5)式可得 0 1 = 0 45 即切应力的极值作用平面与主平面成 450 角。由(10-5)式求出 sin2α1 和 cos2α1,代入(10-2)式, 得切应力的最大和最小值为 2 2 min max 2 x x y + − = (10-6) 【例 10-1】单元体受力如图 10.4(a)所示(应力单位:MPa)。试求:(1)指定斜截面上的应力; (2)主应力和主平面方位;(3)最大切应力。 解:(1)计算斜截面的应力 建立图 10.4(a)所示坐标轴,根据符号规定有:σx=60MPa,σy=-80MPa,τx=35MPa,α=600。将 上述数据代入(10-1)和(10-2)式,可得 cos120 35sin 120 75.3MPa 2 60 80 2 60 80 0 0 6 00 − = − + + − = 图 10.4