
第2章教学方案-平面简单力系平面汇交力系的合成与平衡基本内容力对点之矩,合力矩定理力偶,平面力偶系的简化与平衡、掌握平面汇交力系的合成和平衡方程,求解未知力。教学目掌握力对点之矩,合力矩定理。的掌握力偶系的简化与平衡条件。重点平面汇交力系和力偶系的合成与平衡。、难点
第 2 章 教学方案 ——平面简单力系 基 本 内 容 平面汇交力系的合成与平衡 力对点之矩,合力矩定理 力偶,平面力偶系的简化与平衡 教 学 目 的 1、掌握平面汇交力系的合成和平衡方程,求解未知力。 2、掌握力对点之矩,合力矩定理。 3、掌握力偶系的简化与平衡条件。 重 点 、 难 点 平面汇交力系和力偶系的合成与平衡

第2章平面简单力系当力系中的各力作用线都在同一平面上时,该力系称为平面力系。若平面力系中各力作用线通过同一点时,该力系称为平面汇交力系:若平面力系中的各力均成对构成力偶时,称该力系为平面力偶系。通常将平面汇交力系和平面力偶系称为平面简单力系。2.1平面汇交力系的合成与平衡2.1.1 平面汇交力系合成与平衡的几何法合成依据:力的平行四边形法则或三角形法则。如果是由多个力构成的平面汇交力系,用多边形法则。●方法:将力Fi,…,Fa依次首尾相接,形成一条折线,连接其封闭边,即从Fi的始端指向F4的末端所形成的矢量即为合力,如图2.1(c)所示,此法称为力的多边形法则。fa)(d)图2.1·结论:平面汇交力系可以合成为一个合力,该合力等于力系各力的矢量和,合力的作用线通过汇交点。合力FR可用矢量式表示为FR =F+F,+F,-ZF(2-1)画力多边形时,改变各分力相加的次序,将得到形状不同的力多边形,但最后求得的合力不变,如图2.1(d)所示。·平衡条件:平面汇交力系平衡的充分和必要条件是;该力系的合力等于零。以矢量等式表示为25=0(2-2)平衡的几何条件;平面汇交力系的力多边形自行封闭。【例2-1】支架ABC由横杆AB与支撑杆BC组成,如图2.2(a)所示。A、B、C处均为铰链连接,B端悬挂重物,其重力W=5kN,杆重不计,试求两杆所受的力。解:(1)选择研究对象,以销子B为研究对象(2)受力分析,画受力图。由于AB、BC杆均为二力杆,两端所受的力的作用线必过直杆的轴线。FI、Fz、W组成平面汇交力系,其受力图如图2.2(b)所示。(3)根据平衡几何条件求出未知力。当销子平衡时,三力组成一封闭力三角形,先画W
第 2 章 平面简单力系 当力系中的各力作用线都在同一平面上时,该力系称为平面力系。若平面力系中各力 作用线通过同一点时,该力系称为平面汇交力系;若平面力系中的各力均成对构成力偶时, 称该力系为平面力偶系。通常将平面汇交力系和平面力偶系称为平面简单力系。 2.1 平面汇交力系的合成与平衡 2.1.1 平面汇交力系合成与平衡的几何法 ●合成依据:力的平行四边形法则或三角形法则。如果是由多个力构成的平面汇交力系, 用多边形法则。 ●方法:将力 F1,.,F4 依次首尾相接,形成一条折线,连接其封闭边,即从 F1 的 始端指向 F4 的末端所形成的矢量即为合力,如图 2.1(c)所示,此法称为力的多边形法则。 图 2.1 ●结论:平面汇交力系可以合成为一个合力,该合力等于力系各力的矢量和,合力的作 用线通过汇交点。合力 FR 可用矢量式表示为 = = + + + = n i R n i 1 F F1 F2 F F (2-1) 画力多边形时,改变各分力相加的次序,将得到形状不同的力多边形,但最后求得的合 力不变,如图 2.1(d)所示。 ●平衡条件:平面汇交力系平衡的充分和必要条件是:该力系的合力等于零。以矢量等 式表示为 (2-2) ●平衡的几何条件:平面汇交力系的力多边形自行封闭。 【例 2-1】支架 ABC 由横杆 AB 与支撑杆 BC 组成,如图 2.2(a)所示。A、B、C 处 均为铰链连接,B 端悬挂重物,其重力 W = 5kN,杆重不计,试求两杆所受的力。 解:(1)选择研究对象,以销子 B 为研究对象。 (2)受力分析,画受力图。由于 AB、BC 杆均为二力杆,两端所受的力的作用线必过 直杆的轴线。F1、F2、W 组成平面汇交力系,其受力图如图 2.2(b)所示。 (3)根据平衡几何条件求出未知力。当销子平衡时,三力组成一封闭力三角形,先画 W , 1 0 n i i F = =
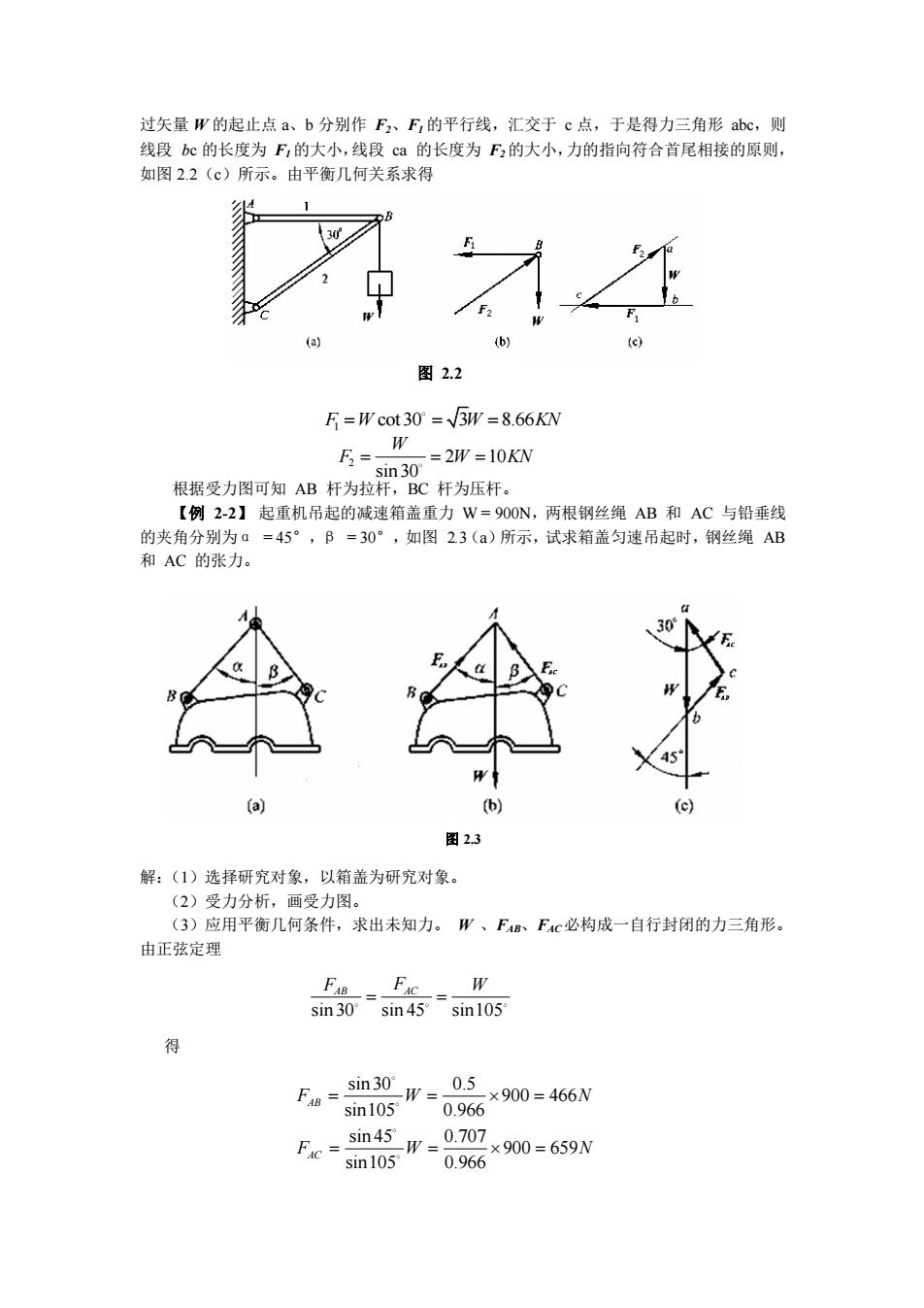
过矢量W的起止点a、b分别作F2、F,的平行线,汇交于c点,于是得力三角形abc,则线段 bc 的长度为Fi的大小,线段 ca 的长度为F的大小,力的指向符合首尾相接的原则,如图2.2(c)所示。由平衡几何关系求得图2.2F =Wcot30°=/3W=8.66KNWF==2W=10KNsin30根据受力图可知AB杆为拉杆,BC杆为压杆。【例2-2】起重机吊起的减速箱盖重力W=900N,两根钢丝绳AB和AC与铅垂线的夹角分别为α=45°,β=30°,如图2.3(a)所示,试求箱盖匀速吊起时,钢丝绳AB和AC的张力。(a)(b)图 2.3解:(1)选择研究对象,以箱盖为研究对象。(2)受力分析,画受力图(3)应用平衡几何条件,求出未知力。W、FAB、FAc必构成一自行封闭的力三角形。由正弦定理o-slsW=sin30 = 0.5900=466NFABsin1050.966=0.707×900= 659Nsin45_w=FAc=sin1050.966
1F W W KN = = = cot30 3 8.66 2 2 10 sin30 W F W KN = = = 图 2.2 过矢量 W 的起止点 a、b 分别作 F2、F1 的平行线,汇交于 c 点,于是得力三角形 abc,则 线段 bc 的长度为 F1 的大小,线段 ca 的长度为 F2 的大小,力的指向符合首尾相接的原则, 如图 2.2(c)所示。由平衡几何关系求得 根据受力图可知 AB 杆为拉杆,BC 杆为压杆。 【例 2-2】 起重机吊起的减速箱盖重力 W = 900N,两根钢丝绳 AB 和 AC 与铅垂线 的夹角分别为α = 45°,β = 30°,如图 2.3(a)所示,试求箱盖匀速吊起时,钢丝绳 AB 和 AC 的张力。 解:(1)选择研究对象,以箱盖为研究对象。 (2)受力分析,画受力图。 (3)应用平衡几何条件,求出未知力。 W 、FAB、FAC必构成一自行封闭的力三角形。 由正弦定理 得 sin 30 sin 45 sin105 FAB FAC W = = sin 30 0.5 900 466 sin105 0.966 sin 45 0.707 900 659 sin105 0.966 AB AC F W N F W N = = = = = = 图 2.3

2.1.2力在直角坐标轴上的投影·概念:设在平面直角坐标系Oxy内有一已知力F,从力F的两端A和B分别向x、y轴作垂线,垂足a、b和a'、b之间的距离再加上适当的正负号分别称为力F在x轴和y轴上的投影,以X和Y表示。并且规定:当从力的始端投影到末端投影的方向与坐标轴的正向相同时,取正号,反之取负。图 2.4(a)中的x、Y均为正值,图2.4(b)中的X、为负值、Y为正值。所以,力在坐标轴上的投影是代数量。(a)(b)图 2.4·计算:力的投影的大小可用三角公式计算,设力F与x轴的正向夹角为α,则X=Fcosα(2-3)Y=Fsinα分力和投影的关系:如将力 F 沿 x、y坐标轴分解,所得分力F、F,的大小与力 F在同轴的投影X、Y的绝对值相等,但必须注意:力的投影与分力是两个不同的概念。力的投影是代数量,而分力是矢量。其关系可表示为F=F,+E,=Xi+Y(2-4)若已知力F在直角坐标轴上的投影X、Y,则可按下式求出该力的大小和方向余弦为F=x+y?(2-5)cosα=2.1.3合力投影定理由n个力构成的平面汇交力系,其合力可由(2-1)式求得。若将合力和各分力表示为式(2-4)的形式,即Fr=Fri+Fryj,F =X,i+Yj (i=-1,2...n)代入式(2-1)可得Fr=Fai+Frj-2xi+2Yj(2-6)即
图 2.4 2.1.2 力在直角坐标轴上的投影 ●概念:设在平面直角坐标系 Oxy 内有一已知力 F,从力 F 的两端 A 和 B 分别向 x、y 轴作垂线,垂足 a、b 和 a′、b′之间的距离再加上适当的正负号分别称为力 F 在 x 轴和 y 轴上的投影,以 X 和 Y 表示。并且规定:当从力的始端投影到末端投影的方向与坐 标轴的正向相同时,取正号,反之取负。图 2.4(a)中的 X、Y 均为正值,图 2.4(b)中 的 X、为负值、Y 为正值。所以,力在坐标轴上的投影是代数量。 ●计算:力的投影的大小可用三角公式计算,设力 F 与 x 轴的正向夹角为α,则 (2-3) ●分力和投影的关系:如将力 F 沿 x、y 坐标轴分解,所得分力 Fx、Fy的大小与力 F 在同轴的投影 X、Y 的绝对值相等,但必须注意:力的投影与分力是两个不同的概念。力 的投影是代数量,而分力是矢量。其关系可表示为 F F F Xi Yj = x + y = + (2-4) 若已知力 F 在直角坐标轴上的投影 X、Y,则可按下式求出该力的大小和方向余弦为 F X F X Y = = + cos 2 2 (2-5) 2.1.3 合力投影定理 由 n 个力构成的平面汇交力系,其合力可由(2-1)式求得。若将合力和各分力表示为 式(2-4)的形式,即 F F , X Y (i 1,2 n) FR = Rx i + Ry j Fi = i i + i j = 代入式(2-1)可得 F i j i j = = = + = + n i i n i R FRx FRy Xi Y 1 1 (2-6) 即 cos sin X F Y F = =

V(2-7)?可得结论:合力在任一轴上的投影等于各分力在同一轴上的投影的代数和。这就是合力投影定理。2.1.4平面汇交力系合成与平衡的解析法●合成:设在刚体上的点O处,作用了由n个力Fi,F2,,F,组成的平面汇交力系,Xi和Y,X2和Y2,…,X和Yn分别表示力Fi,F2,,Fa在直角坐标轴Ox和Oy上的投影。根据合力投影定理,可求得合力FR在这两轴上的投影,如式(2-7)所示。已知力的投影,可以根据式(2-5)求得合力的大小和方向为Fr=F+F=Zx)+(Zm)(2-8)Zxcosα式中的α表示合力的正向与x轴所夹的角。【例2-3】一吊环受到三条钢丝绳的拉力,如图2.5(a)所示。已知Fi=2000N,平向左;Fz-2500N,与水平成30°角;F:=1500N,铅垂向下,试用解析法求合力的大小和方向。(6)fa图2解:以三力的交点0为坐标原点,建立直角坐标系如图2.5所示,先分别计算各力的投影。Fx =-F, =-2000NF2=-F,cos30=-2500×0.866=-2165NFI=0F,=0Fz, =-F, sin30°=-2500×0.5=-1250NF,=-F, =-1500N可得R, =F, =(-2000-2165+0)=-4165NR,=ZF,=(0-1250-1500)=-2750NR=R +R, = /-4165) +(-2750) =4991N
= = = = n i Ry i n i Rx i F Y F X 1 1 (2-7) 可得结论:合力在任一轴上的投影等于各分力在同一轴上的投影的代数和。这就是合力 投影定理。 2.1.4 平面汇交力系合成与平衡的解析法 ●合成:设在刚体上的点 O 处,作用了由 n 个力 F1,F2,.,Fn组成的平面汇交力 系,X1 和 Y1,X2 和 Y2,.,Xn 和 Yn 分别表示力 F1,F2,.,Fn 在直角坐标轴 Ox 和 Oy 上的投影。根据合力投影定理,可求得合力 FR 在这两轴上的投影,如式(2-7)所示。 已知力的投影,可以根据式(2-5)求得合力的大小和方向为 R R Rx Ry F X F F F X Y = = + = + cos ( ) ( ) 2 2 2 2 (2-8) 式中的α 表示合力的正向与 x 轴所夹的角。 【例 2-3】 一吊环受到三条钢丝绳的拉力,如图 2.5(a)所示。已知 F1=2000N,水 平向左;F2=2500N,与水平成 30°角;F3=1500N,铅垂向下,试用解析法求合力的大小和 方向。 图 2.5 解:以三力的交点 O 为坐标原点,建立直角坐标系如图 2.5 所示,先分别计算各力的 投影。 可得 1 1 2 2 3 1 2 2 3 3 2000 cos30 2500 0.866 2165 0 0 sin 30 2500 0.5 1250 1500 X x x y y y F F N F F N F F F F N F F N = − = − = − = − = − = = = − = − = − = − = − 2 2 2 2 ( 2000 2165 0) 4165 (0 1250 1500) 2750 ( 4165) ( 2750) 4991 x x y y x y R F N R F N R R R N = = − − + = − = = − − = − = + = − + − =