
第4章教学方案-空间力系基本内容空间汇交力系空间力偶系力对点的矩与力对轴的矩空间任意力系了解空间汇交力系的合成与平衡条件。教了解空间力偶系的合成与平衡。学目、了解空间力对点的矩和空间力对轴的矩及它们的关系,的、了解空间任意力系的简化、合成与平衡。重点力对轴之矩及力对点之矩;空间力系的简化。难点
第 4 章 教学方案 ——空间力系 基 本 内 容 空间汇交力系 空间力偶系 力对点的矩与力对轴的矩 空间任意力系 教 学 目 的 1、了解空间汇交力系的合成与平衡条件。 2、了解空间力偶系的合成与平衡。 3、了解空间力对点的矩和空间力对轴的矩及它们的关系。 4、了解空间任意力系的简化、合成与平衡。 重 点 、 难 点 力对轴之矩及力对点之矩;空间力系的简化

第4章空间力系作用在物体上的力系,若其作用线在空间分布,称为空间力系。空间力系是最一般的力系,平面力系只是它的特例。在工程实际中遇到的空间力系有各种形式,当力系中各力作用线汇交于一点时称为空间汇交力系;当力系中的力全部构成空间力偶时称为空间力偶系;当力系中各力作用线在空间任意分布时称为空间任意力系。4.1空间汇交力系4.1.1力在空间直角坐标轴上的投影和分力空间力系的研究方法与平面力系基本相同,只是将平面问题中的概念、理论和方法推广和引伸到空间问题中。若已知力F与空间直角坐标系Oxy=的x、y、=轴正向的夹角分别为α、β、,如图4.1所示,则力在三个坐标轴上的投影分别为90图 4.1图4.2X=FcosαY=Fcosβ(4-1)Z=Fcosy若已知力F与=轴正向的夹角和力作用线与=轴所构成的平面与Ox=坐标平面的夹角p,如图4.2所示,则可以先将F力投影到Oxy平面上,然后再向x、轴投影。力在三个坐标轴上的投影分别为X = Fsin ycosY=Fsinysn g(4-2)Z=Fcosy若以 F、F、F:表示力F在坐标轴方向的分力,则F=F,+E,+F,=Xi+Y+Zk(4-3)
第 4 章 空间力系 作用在物体上的力系,若其作用线在空间分布,称为空间力系。空间力系是最一般的 力系,平面力系只是它的特例。在工程实际中遇到的空间力系有各种形式,当力系中各力作 用线汇交于一点时称为空间汇交力系;当力系中的力全部构成空间力偶时称为空间力偶系; 当力系中各力作用线在空间任意分布时称为空间任意力系。 4.1 空间汇交力系 4.1.1 力在空间直角坐标轴上的投影和分力 空间力系的研究方法与平面力系基本相同,只是将平面问题中的概念、理论和方法推广 和引伸到空间问题中。 若已知力 F 与空间直角坐标系 Oxyz 的 x、y、z 轴正向的夹角分别为 α、β、γ,如图 4.1 所示,则力在三个坐标轴上的投影分别为 = = = cos cos cos Z F Y F X F (4-1) 若已知力 F 与 z 轴正向的夹角 γ 和力作用线与 z 轴所构成的平面与 Oxz 坐标平面的夹角 φ,如图 4.2 所示,则可以先将 F 力投影到 Oxy 平面上,然后再向 x、y 轴投影。力在三个坐 标轴上的投影分别为 = = = cos sin sin sin cos Z F Y F X F (4-2) 若以 Fx、Fy、Fz 表示力 F 在坐标轴方向的分力,则 F = Fx + Fy + Fz = Xi + Yj + Zk (4-3) 图 4.1 图 4.2
其中,i、小、k分别为x、少、三坐标轴方向的单位矢量。可见,分力的大小就等于同方向的投影的绝对值。若已知力F在三个直角坐标轴上的投影X、Y、Z,则力F的大小和方向余弦为F =/x2 +y2 +z2X-Ecosα(4-4)POscosy4.1.2空间汇交力系的合成与平衡条件·空间汇交力系可以合成为一个合力,该合力等于力系各分力的矢量和,合力作用线过汇交点。即FR=F+F,+.+F,-ZF(4-5)根据(4-3)式可得Fr =2xi+2yj+Ezk(4-6)可见,合力FR在x、y、=坐标轴上的投影为ZX、Yi、Z。由此得合力的大小和方向余弦为Fr=Ex)+()+(Zz)co(Fa.i)- (4-7)22cos(Fr,k) =FR·空间汇交力系平衡的充分必要条件是:力系的合力等于零,即Fr=ZF,=0(4-8)因此可得空间汇交力系的平衡方程为Zx =0]ZY=0(4-9)Zz=0空间汇交力系有三个独立平衡方程,可以求解三个未知量。【例4-1】由三根无重直杆组成的挂物架如图4.3所示。各点光滑铰链连接,BOC平面是水平面,且OB=OC,角度如图。若O点所挂重物图 4.3
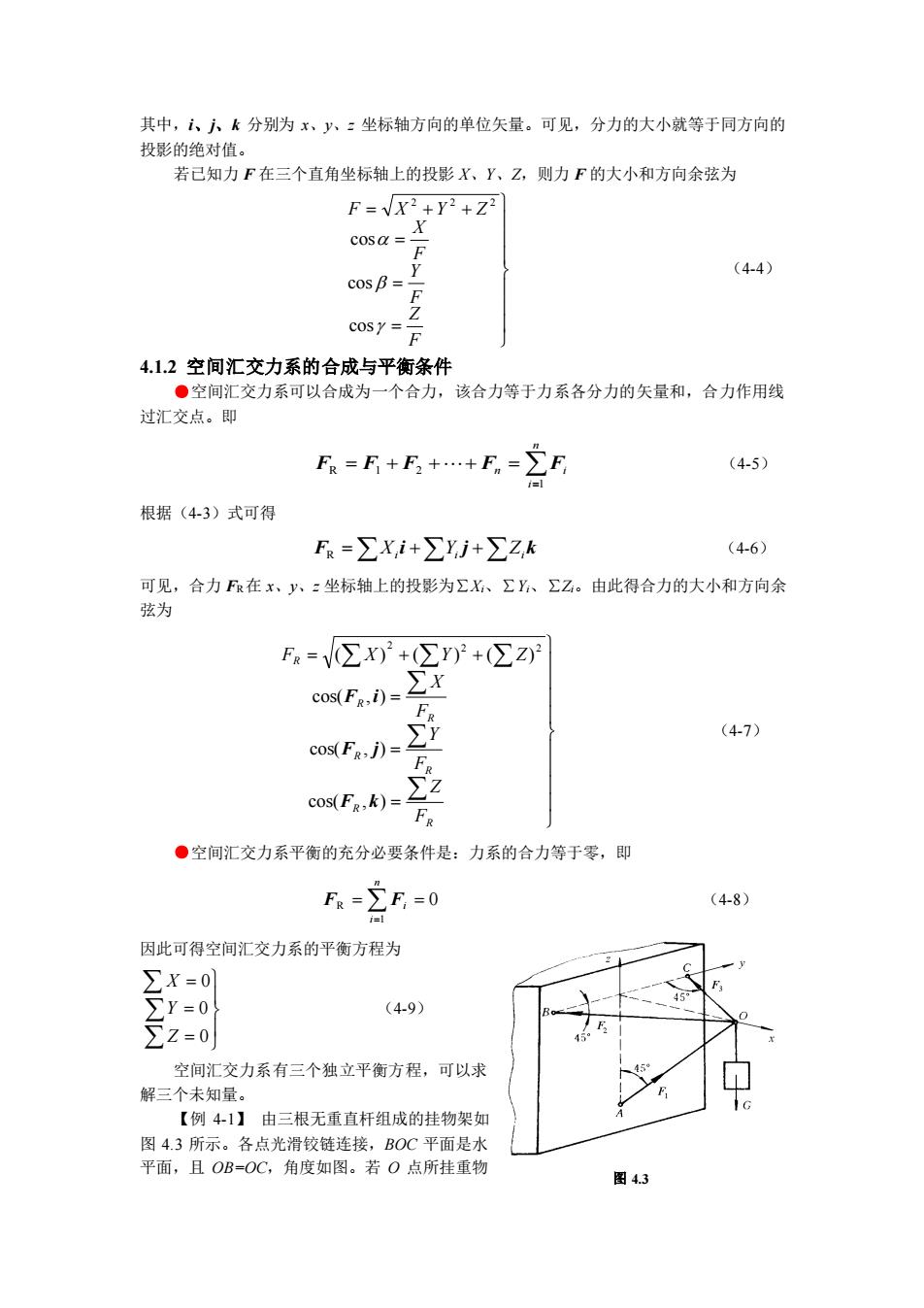
图 4.3 其中,i、j、k 分别为 x、y、z 坐标轴方向的单位矢量。可见,分力的大小就等于同方向的 投影的绝对值。 若已知力 F 在三个直角坐标轴上的投影 X、Y、Z,则力 F 的大小和方向余弦为 = = = = + + F Z F Y F X F X Y Z cos cos cos 2 2 2 (4-4) 4.1.2 空间汇交力系的合成与平衡条件 ●空间汇交力系可以合成为一个合力,该合力等于力系各分力的矢量和,合力作用线 过汇交点。即 = = + + + = n i n i 1 FR F1 F2 F F (4-5) 根据(4-3)式可得 FR =Xi i +Yi j +Zik (4-6) 可见,合力 FR在 x、y、z 坐标轴上的投影为∑Xi、∑Yi、∑Zi。由此得合力的大小和方向余 弦为 = = = = + + R R R R R R R F Z F Y F X F X Y Z cos( , ) cos( , ) cos( , ) ( ) ( ) ( ) 2 2 2 F k F j F i (4-7) ●空间汇交力系平衡的充分必要条件是:力系的合力等于零,即 0 1 R = = = n i F Fi (4-8) 因此可得空间汇交力系的平衡方程为 = = = 0 0 0 Z Y X (4-9) 空间汇交力系有三个独立平衡方程,可以求 解三个未知量。 【例 4-1】 由三根无重直杆组成的挂物架如 图 4.3 所示。各点光滑铰链连接,BOC 平面是水 平面,且 OB=OC,角度如图。若 O 点所挂重物

重G=1000N,求三杆所受的力。解:(1)取整个系统研究,分析受力由于三杆均不计自重且两端受力,为二力杆,所以A、B、C三点约束力方向沿杆的方向,如图4.3所示(2)建立图示坐标系,列平衡方程ZX=02y=0ZZ=0得[F, sin 45°- E sin 45° - F sin 45°= 0- F, cos45° +F, cos45° = 0F, cos45°-G=0代入数据,解得Fi=1414NF2=F3=707N4.2空间力偶系4.2.1空间力偶的矢量表示,力偶的作用效果不仅与力偶矩在空间情况下的大小、力偶的转向有关,也与力偶作用面的方位有关。如果两个力偶的力偶矩大小相等,但作用面不平行,两力偶的作用效果也不同。因此,空间力偶包括力偶矩的大小、力偶的转向和力偶作用面方位三个要素,通常可以用一个失量表示。矢量的长度表示力偶矩的大小,矢量线垂直于力偶作用平面图4.4(即力偶作用平面的法线),矢量的箭头指向与力偶的转向服从右手螺旋法则,如图4.4所示。该矢量称为力偶矩矢,力偶对刚体的作用完全由力偶矩矢确定。力偶矩失是自由失量,可以在刚体上平行移动,而不改变对刚体的作用效果。如果两个力偶的力偶矩矢相等,则两个力偶对刚体的作用效果相同,两个力偶等效。4.2.2空间力偶系的合成与平衡●设由 n个空间力偶Mi、M2、、M,构成的空间力偶系。可以证明,该力系可以合成为一个合力偶,合力偶的力偶矩矢等于各分力偶矩矢的矢量和,即M=M,+M,+.+M,-ZM.(4-10)如果同力一样,力偶矩矢也表达为解析表达式M=Mi+M,j+M.k(4-11)其中Ms、My、M为力偶矩矢在x、y、z轴上的投影。则(4-10)式可以表示为
图 4.4 重 G=1000N,求三杆所受的力。 解:(1)取整个系统研究,分析受力 由于三杆均不计自重且两端受力,为二力杆,所以 A、B、C 三点约束力方向沿杆的方 向,如图 4.3 所示。 (2)建立图示坐标系,列平衡方程 = = = 0 0 0 Z Y X 得 − = − + = − − = cos 45 0 cos 45 cos 45 0 sin 45 sin 45 sin 45 0 0 1 0 3 0 2 0 3 0 2 0 1 F G F F F F F 代入数据,解得 F1=1414N F2=F3=707N 4.2 空间力偶系 4.2.1 空间力偶的矢量表示 在空间情况下,力偶的作用效果不仅与力偶矩 的大小、力偶的转向有关,也与力偶作用面的方位 有关。如果两个力偶的力偶矩大小相等,但作用面 不平行,两力偶的作用效果也不同。因此,空间力 偶包括力偶矩的大小、力偶的转向和力偶作用面方 位三个要素,通常可以用一个矢量表示。矢量的长 度表示力偶矩的大小,矢量线垂直于力偶作用平面 (即力偶作用平面的法线),矢量的箭头指向与力偶的 转向服从右手螺旋法则,如图 4.4 所示。该矢量称为力偶矩矢,力偶对刚体的作用完全由力 偶矩矢确定。 力偶矩矢是自由矢量,可以在刚体上平行移动,而不改变对刚体的作用效果。 如果两个力偶的力偶矩矢相等,则两个力偶对刚体的作用效果相同,两个力偶等效。 4.2.2 空间力偶系的合成与平衡 ●设由 n 个空间力偶 M1、M2、.、Mn 构成的空间力偶系。可以证明,该力系可以合 成为一个合力偶,合力偶的力偶矩矢等于各分力偶矩矢的矢量和,即 = = + + + = n i n i 1 M M1 M2 M M (4-10) 如果同力一样,力偶矩矢也表达为解析表达式 M = M x i + M y j + M zk (4-11) 其中 Mx、My、Mz 为力偶矩矢在 x、y、z 轴上的投影。则(4-10)式可以表示为

(4-12)M=(EM)i+EM)j+(EM.)k合力偶矩矢的大小和方向余弦也可用下列公式求出M=/M.)+(2M,)*+(2M.)cos(M,i)-ZMM.(4-13)cos(M,j) = 2M.cos(M,k) =M·空间力偶系平衡的充分必要条件为:该力系的合力偶矩失等于零,也就是该力系的所有力偶矩矢的矢量和等于零。即≥M,=0(4-14)根据(4-13)式,上式可进一步表示为Mx= 0)(4-15)三个独立平衡方程可以解三个未知量。这就是空间力偶系的平衡方程4.3力对点的矩与力对轴的矩4.3.1空间力对点的矩的失量表示力对点的矩的作用效果不仅与力矩的大小和转向有关,而且与力与矩心所在的平面(力矩作用面)的方位有关。在空间力系中,力矩作用面是空间内的某一平面,要表达力矩的大小、转向和作用面方位三个要素,应该用一个矢量表示。其中矢量的模等于力的大小与矩心到力作用线的垂直距离h(力臂)的乘积;矢量的方位和力矩作用面的法线的方位相同:矢量的指向是根据力矩的转向按右手螺旋法则确定。力F对O点的矩的矢量用Mo(F)表示,如图4.5所示。力矩的大小为Mo(F)= Fh= 2So4B1式中SaBc为三角形 OAB的面积。若用r表示力F作用点A的失径,则rXF也是一个矢量,其大小等于三角形O.AB的面积.V.?的两倍,方位垂直于,与F所组成的平面,指向也由右手螺旋法则确定。可见hC(4-16)Mo (F) =rXF若在矩心0处建立空间直角坐标系Oxyz坐标方向的单位失量用么、小、k表示,力作用点图 4.5
图 4.5 M = (Mix )i + (Miy ) j + (Miz )k (4-12) 合力偶矩矢的大小和方向余弦也可用下列公式求出 = = = = + + M M M M M M M M M M i z i y i x i x i y i z cos( , ) cos( , ) cos( , ) ( ) ( ) ( ) 2 2 2 M k M j M i (4-13) ●空间力偶系平衡的充分必要条件为:该力系的合力偶矩矢等于零,也就是该力系的 所有力偶矩矢的矢量和等于零。即 0 1 = = n i Mi (4-14) 根据(4-13)式,上式可进一步表示为 = = = 0 0 0 iz iy ix M M M (4-15) 这就是空间力偶系的平衡方程。三个独立平衡方程可以解三个未知量。 4.3 力对点的矩与力对轴的矩 4.3.1 空间力对点的矩的矢量表示 力对点的矩的作用效果不仅与力矩的大小和转向有关,而且与力与矩心所在的平面 (力矩作用面)的方位有关。在空间力系中,力矩作用面是空间内的某一平面,要表达力 矩的大小、转向和作用面方位三个要素,应该用一个矢量表示。其中矢量的模等于力的大 小与矩心到力作用线的垂直距离 h(力臂)的乘积;矢量的方位和力矩作用面的法线的方 位相同;矢量的指向是根据力矩的转向按右手螺旋法则确定。力 F 对 O 点的矩的矢量用 MO(F)表示,如图 4.5 所示。 力矩的大小为 MO F = Fh = 2SOAB ( ) 式中 SΔABC为三角形 OAB 的面积。 若用 r 表示力 F 作用点 A 的矢径,则 r×F 也是一个矢量,其大小等于三角形 OAB 的面积 的两倍,方位垂直于 r 与 F 所组成的平面,指向 也由右手螺旋法则确定。可见 MO(F)= r×F (4-16) 若在矩心 O 处建立空间直角坐标系 Oxyz, 坐标方向的单位矢量用 i、j、k 表示,力作用点