
第13 章教学方案压杆稳定压杆稳定性的概念基本内容细长压杆的临界压力临界应力和柔度三种不同类型的压杆压杆的稳定校核教学目1、了解平衡稳定性的概念,掌握压杆稳定的基本概念。2、掌握细长压杆临界压力的欧拉公式。3、掌握临界应力与柔度的概念,了解三类不同的压杆。的4、了解压杆稳定安全准则。重点压杆稳定的基本概念;压杆的临界力的计算。难点
第 13 章 教学方案 ——压杆稳定 基 本 内 容 压杆稳定性的概念 细长压杆的临界压力 临界应力和柔度 三种不同类型的压杆 压杆的稳定校核 教 学 目 的 1、了解平衡稳定性的概念,掌握压杆稳定的基本概念。 2、掌握细长压杆临界压力的欧拉公式。 3、掌握临界应力与柔度的概念,了解三类不同的压杆。 4、了解压杆稳定安全准则。 重 点 、 难 点 压杆稳定的基本概念;压杆的临界力的计算
第 13 章 压杆稳定13.1压杆稳定性的概念13.1.1平衡稳定性的概念处于平衡状态的系统,若受到外界干扰偏离平衡位置后,在干扰撤除后仍能回到平衡位置,则其平衡是稳定的;若不能回到平衡位置而失去平衡状态则为不稳定的平衡;若在任意位置保持平衡则为随遇平衡。例如,小球放在凹面、凸面和平面上的状态。13.1.2压杆的稳定性前面的研究中,受压直杆失效表现为强度不足,即杆件塑性屈服或脆性断裂。事实上,对于较长的受压直杆,常出现另一种与强度失效完全不同的破坏形式,就是在使用中突然变弯甚至折断。这种破坏形式称为失稳。为了保证压杆工作的安全性,在设计压杆时,必须考虑其稳定性。工程结构中有许多受压的细长杆,例如内燃机配气机构中的挺杆(图13.2),磨床液压装置的活塞杆(图13.3)。还有桁架结构中的抗压杆,建筑物中的柱也是压杆。实践证明,导致细长受压杆件失稳破坏的轴向力要比其发生强度破坏时的轴向力小得多,可见这种形式的失效,并非强度不足,而是稳定性不够典乡西EPE活塞杆图 13.3图 13.213.1.3细长压杆的失稳现象轴向受压的理想细长直杆如图13.4所示,当压力F小于某一极限力时,它保持直线状态的平衡。若对杆施加一微小的横向干扰力O,杆将发生微小的弯曲变形,如图13.4(a)中虚线所示,当撤去横向力0后,它将回复到原有的直线状态,如图13.4(b)。此时,压杆处于稳定的直线平衡状态。若逐渐增大压力F,达到某一极限值Fa时,在微小的干扰力的α作用下,压杆将产生微小的弯曲,当撤去横向力后,仍将保持曲线状态的平衡,如图13.4(c)所示。此时,压杆处于失稳的临界状态上述现象表明,当轴向压力F小于某一极限值时,压杆直线状态的平衡是稳定的,当F值达到该极限值时,压杆原有的直线状态的平衡将变为不稳定。这个极限压力值是使压杆直线状态的平衡开始由稳定转(a)(b)变为不稳定的临界值,称为临界压力或临界力,用Fa表示。压杆由直线图13.4状态的稳定平衡转变为不稳定平衡,称为丧失稳定,简称失稳
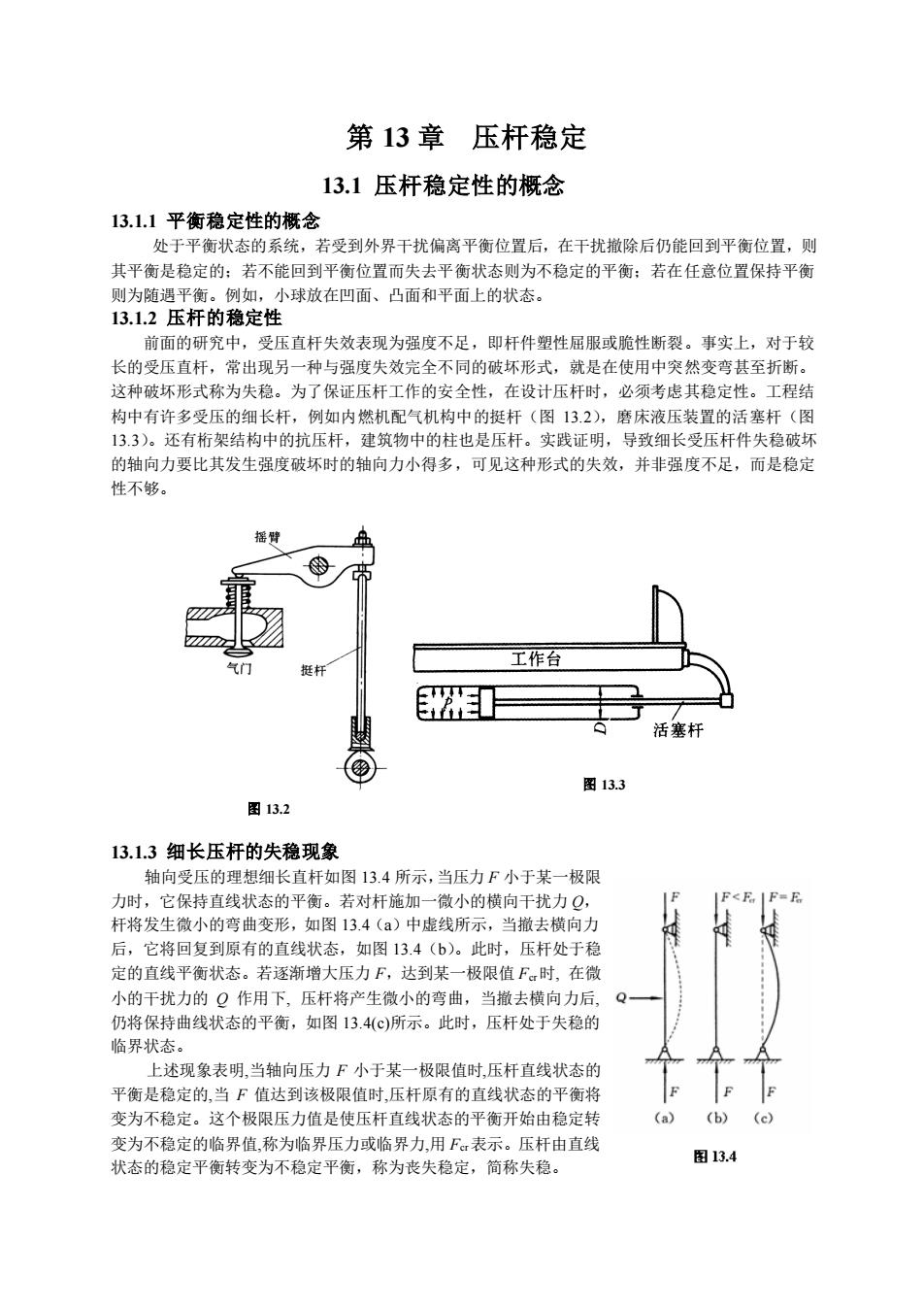
第 13 章 压杆稳定 13.1 压杆稳定性的概念 13.1.1 平衡稳定性的概念 处于平衡状态的系统,若受到外界干扰偏离平衡位置后,在干扰撤除后仍能回到平衡位置,则 其平衡是稳定的;若不能回到平衡位置而失去平衡状态则为不稳定的平衡;若在任意位置保持平衡 则为随遇平衡。例如,小球放在凹面、凸面和平面上的状态。 13.1.2 压杆的稳定性 前面的研究中,受压直杆失效表现为强度不足,即杆件塑性屈服或脆性断裂。事实上,对于较 长的受压直杆,常出现另一种与强度失效完全不同的破坏形式,就是在使用中突然变弯甚至折断。 这种破坏形式称为失稳。为了保证压杆工作的安全性,在设计压杆时,必须考虑其稳定性。工程结 构中有许多受压的细长杆,例如内燃机配气机构中的挺杆(图 13.2),磨床液压装置的活塞杆(图 13.3)。还有桁架结构中的抗压杆,建筑物中的柱也是压杆。实践证明,导致细长受压杆件失稳破坏 的轴向力要比其发生强度破坏时的轴向力小得多,可见这种形式的失效,并非强度不足,而是稳定 性不够。 13.1.3 细长压杆的失稳现象 轴向受压的理想细长直杆如图 13.4 所示,当压力 F 小于某一极限 力时,它保持直线状态的平衡。若对杆施加一微小的横向干扰力 Q, 杆将发生微小的弯曲变形,如图 13.4(a)中虚线所示,当撤去横向力 后,它将回复到原有的直线状态,如图 13.4(b)。此时,压杆处于稳 定的直线平衡状态。若逐渐增大压力 F,达到某一极限值 Fcr时, 在微 小的干扰力的 Q 作用下, 压杆将产生微小的弯曲,当撤去横向力后, 仍将保持曲线状态的平衡,如图 13.4(c)所示。此时,压杆处于失稳的 临界状态。 上述现象表明,当轴向压力 F 小于某一极限值时,压杆直线状态的 平衡是稳定的,当 F 值达到该极限值时,压杆原有的直线状态的平衡将 变为不稳定。这个极限压力值是使压杆直线状态的平衡开始由稳定转 变为不稳定的临界值,称为临界压力或临界力,用 Fcr表示。压杆由直线 状态的稳定平衡转变为不稳定平衡,称为丧失稳定,简称失稳。 图 13.2 图 13.3

10.2细长压杆的临界压力13.2.1两端铰支细长压杆的临界压力设两端铰支长度为1的细长杆,在轴向压力F的作用下保持微弯平衡状态,如图13.5所示。在图所示坐标系中,x截面处横截面上的弯矩为M(a)=-Fw(a)-图 13.5小变形下挠曲线近似微分方程为12w=M(c)(b) dr将(a)式代入(b)式,得CI-Fw(c)若令K=EI(d)式(c)可写成dw+kw=0(e).2此微分方程的通解为= Asin kx+ Bcos kx(f)上式中的A、B为待定常数,可由杆端边界条件确定。在x=0处,W=0,代入式(f),得B=0于是式(f)改写为w= Asin kx(g)上式表示挠曲线为一正弦曲线。在x=1处,W=0,代入式(g),则有Asin kl=0可得A=0或sinkl=0A=0时,W=0,表示压杆未发生弯曲,这与杆产生微弯曲的前提矛盾。由此必有sin kl= 0
10.2 细长压杆的临界压力 13.2.1 两端铰支细长压杆的临界压力 设两端铰支长度为 l 的细长杆,在轴向压力 F 的作用下保持微弯平衡状态,如图 13.5 所示。在 图所示坐标系中, x 截面处横截面上的弯矩为 M(x) = −Fw (a) 小变形下挠曲线近似微分方程为 M (x) dx d w EI = 2 2 (b) 将(a)式代入(b)式,得 Fw dx d w EI = − 2 2 (c) 若令 EI F k = 2 (d) 式(c)可写成 0 2 2 2 + k w = dx d w (e) 此微分方程的通解为 w = Asin kx+ Bcoskx (f) 上式中的 A、B 为待定常数,可由杆端边界条件确定。在 x = 0 处, w = 0 ,代入式(f),得 B=0 于是式(f)改写为 w = Asin kx (g) 上式表示挠曲线为一正弦曲线。在 x = l 处, w = 0 ,代入式(g),则有 Asin kl = 0 可得 A = 0或sin kl = 0 A=0 时, w = 0,表示压杆未发生弯曲,这与杆产生微弯曲的前提矛盾。由此必有 sin kl = 0 图 13.5

可得kl=n元(n = ,.,.,.)_n元或(h)将式(d)代入上式,可得F=n'r'El(i)(. = ,,.,.)72上式表明,当压杆处于微弯平衡状态时,在理论上压力F是多值的。由于临界压力应是压杆在微弯形状下保持平衡的最小轴向力,所以在上式中取不等于零的F 最小值。因此,取n=1,可得临界压力为Fo=T'E(13-1)上式一般称为两端铰支细长压杆临界压力的欧拉公式。13.2.2 其它支座条件下细长压杆的临界压力通过类比可以得到其它杆端约束条件下压杆的压杆临界力的表达式。综合各种约束情况,可将欧拉公式写成统一的形式Fo=T'El(13-2)(ul)式中ul称为相当长度,表示将杆端约束条件不同的压杆长度1折算成两端铰支压杆的长度,μ称为长度因数。几种杆端约束情况下长度因数μ值列于表13-1中,从表13-1中可以看出,两端铰支时,在临界力作用下,压杆挠曲线为正弦半波曲线。而一端固定、另一端自由长为1的压杆的挠曲线与长为2/的两端铰支的压杆的挠曲线的一半形状相同。因此,在这种约束情况下,相当长度为21。其它约束情况下的长度因数可依此类推。这里需注意,压杆挠曲线拐点处弯矩为零,这相当于杆端铰支约束的情况。表 13-1 压杆长度因数1EH两端铰支两端固定0.5一值2i3挑曲线形状中A
可得 kl = n (n = 0,1,2, ) 或 2 2 2 2 l n k = (h) 将式(d)代入上式,可得 ( 0,1,2, ) 2 2 2 = n = l n EI F (i) 上式表明,当压杆处于微弯平衡状态时,在理论上压力 F 是多值的。由于临界压力应是压杆在 微弯形状下保持平衡的最小轴向力,所以在上式中取不等于零的 F 最小值。因此,取 n =1 ,可得临 界压力为 Fcr= 2 2 l EI (13-1) 上式一般称为两端铰支细长压杆临界压力的欧拉公式。 13.2.2 其它支座条件下细长压杆的临界压力 通过类比可以得到其它杆端约束条件下压杆的压杆临界力的表达式。综合各种约束情况,可将 欧拉公式写成统一的形式 ( ) 2 2 l EI Fcr = (13-2) 式中 μ l 称为相当长度,表示将杆端约束条件不同的压杆长度 l 折算成两端铰支压杆的长度,μ 称为 长度因数。几种杆端约束情况下长度因数 μ 值列于表 13-1 中,从表 13-1 中可以看出,两端铰支时, 在临界力作用下,压杆挠曲线为正弦半波曲线。而一端固定、另一端自由长为 l 的压杆的挠曲线与长 为 2 l 的两端铰支的压杆的挠曲线的一半形状相同。因此,在这种约束情况下,相当长度为 2 l 。其 它约束情况下的长度因数可依此类推。这里需注意,压杆挠曲线拐点处弯矩为零,这相当于杆端铰 支约束的情况。 表 13-1 压杆长度因数

【例13-1】一矩形截面细长压杆,截面宽度b=40mm,高度h=60mm,两端用图示夹头约束。在x-y平面内弯曲时,两端可简化为铰支,如图13.6(a),长度1=2.4m,在x=平面内弯曲时,两端可视为固定端,如图13.6(b),长度,=2.3m。压杆材料为Q235钢,弹性模量E=210GPa。试用欧拉公式求压杆的临界力。t%(a)E上图 13.6解:(1)计算x-y平面内弯曲时的临界压力。由于两端为铰支,因此其长度因数μ=1,由式(13-2)可得临界压力BLb%/2元×210×10×40×60*×10=259(K)FL:(ul)?(ua)?(1×2.4)×12(2)计算x-=平面内弯曲时的临界压力。由于两端为固定支座,其长度因数u=0.5,由式(13-2)可得临界压力元El元Ehb/12元×210×10×60×40°×10-12F" = 501.5(KN)(ul.)?(u,)(0.5×2.3) ×12(3)确定压杆的临界压力。比较上面两种情况下的临界压力,由于F<F,可知压杆首先在x-y平面内失稳。故该压杆的临界压力为Fa=259KN。4)讨论。如果从压杆的强度考虑,对于Q235钢,其g=240MPa,使该压杆塑性屈服而破坏的轴向压力为F,=0,4=0,bh=240×10°×40×60×10-=576(KN)可见,该压杆的Fa远小于F.值,说明细长压杆的承载能力往往是由它的稳定性来决定的。13.3 临界应力和柔度三种不同类型的压杆13.3.1 临界应力和柔度压杆的临界压力Fa除以其横截面面积,定义为压杆的临界应力,即C=Fa将式(13-2)代入上式,得
【例 13-1】一矩形截面细长压杆,截面宽度 b=40mm,高度 h=60mm,两端用图示夹头约束。在 x-y 平面内弯曲时,两端可简化为铰支,如图 13.6(a),长度 l = 2.4m ,在 x-z 平面内弯曲时,两端 可视为固定端,如图 13.6(b),长度 l 1 = 2.3m 。压杆材料为 Q235 钢,弹性模量 E=210GPa。试用欧 拉公式求压杆的临界力。 解:(1)计算 x-y 平面内弯曲时的临界压力。由于两端为铰支,因此其长度因数μ=1,由式(13-2) 可得临界压力 ( ) ( ) ( ) (KN) l Ebh l EI F z cr 259 1 2.4 12 /12 210 10 40 60 10 2 2 9 3 1 2 2 2 3 2 2 = = = = − (2)计算 x-z 平面内弯曲时的临界压力。由于两端为固定支座,其长度因数μ=0.5,由式(13-2) 可得临界压力 ( ) ( ) ( ) (KN) l Ehb l EI F y cr 501.5 0.5 2.3 12 /12 210 10 60 40 10 2 2 9 3 1 2 2 1 2 3 2 1 2 = = = = − (3)确定压杆的临界压力。比较上面两种情况下的临界压力,由于 Fcr Fcr ,可知压杆首先 在 x-y 平面内失稳。故该压杆的临界压力为 Fcr=259KN。 (4)讨论。如果从压杆的强度考虑,对于 Q235 钢,其 σs=240MPa,使该压杆塑性屈服而破坏 的轴向压力为 F A bh (KN) u s s 240 10 40 60 10 576 6 6 = = = = − 可见,该压杆的 Fcr远小于 Fu 值,说明细长压杆的承载能力往往是由它的稳定性来决定的。 13.3 临界应力和柔度 三种不同类型的压杆 13.3.1 临界应力和柔度 压杆的临界压力 Fcr除以其横截面面积,定义为压杆的临界应力,即 A Fcr cr = 将式(13-2)代入上式,得 图 13.6