
S2.1数列极限与函数极限 一、数列极限 例如:(1).2,4,8,.,2”,. {2"} 发散 111 1 (2). 2482. 收敛 (3). 1,-1,1,.,(-101, (-1)-} 发散 (4). 214 收敛
一、数列极限 §2.1 数列极限与函数极限 2,4,8, ,2 , ; 例如: n (1). 1 1 1 1 (2). , , , , , ; 2 4 8 2n 1 (3). 1, 1,1, ,( 1) , ; n+ − − 1 1 4 ( 1) (4). 2, , , ,1 , ; 2 3 n n − − + − + − n n 1 ( 1) 1 {( 1) } −1 − n {2 } n } 2 1 { n 收敛 发散 收敛 发散

§2.1数列极限与函数极限 例如芝诺悖论: 阿基里斯追上乌龟所必须跑过的路程为 11 S=10+1+ 010*= 10_10 1-g1-I9 (米). 10 所以,阿基里斯只要坚持跑到11.2米的路程就可以追上乌龟! 例如截杖问题: 当n无限增大时,无限接近于0
1 1 . 0. 2 2 n n n l n = 当 无限增大时, 无限接近于 例如截杖问题: 例如芝诺悖论: 阿基里斯追上乌龟所必须跑过的路程为 1 1 1 10 100 10 1 ( 10 100 1 9 1 1 10 a S q = + + + + = = = − − 米). 所以,阿基里斯只要坚持跑到11.2米的路程就可以追上乌龟! §2.1 数列极限与函数极限
S2.1数列极限与函数极限 一、 数列极限 “无限接近”意味着什么? 如何用数学用数学语言来刻画? 距离! {an无限接近于常数a, 1an-a任意小(n→o), ,=1+a1非骨0a-→9a风为数 .0
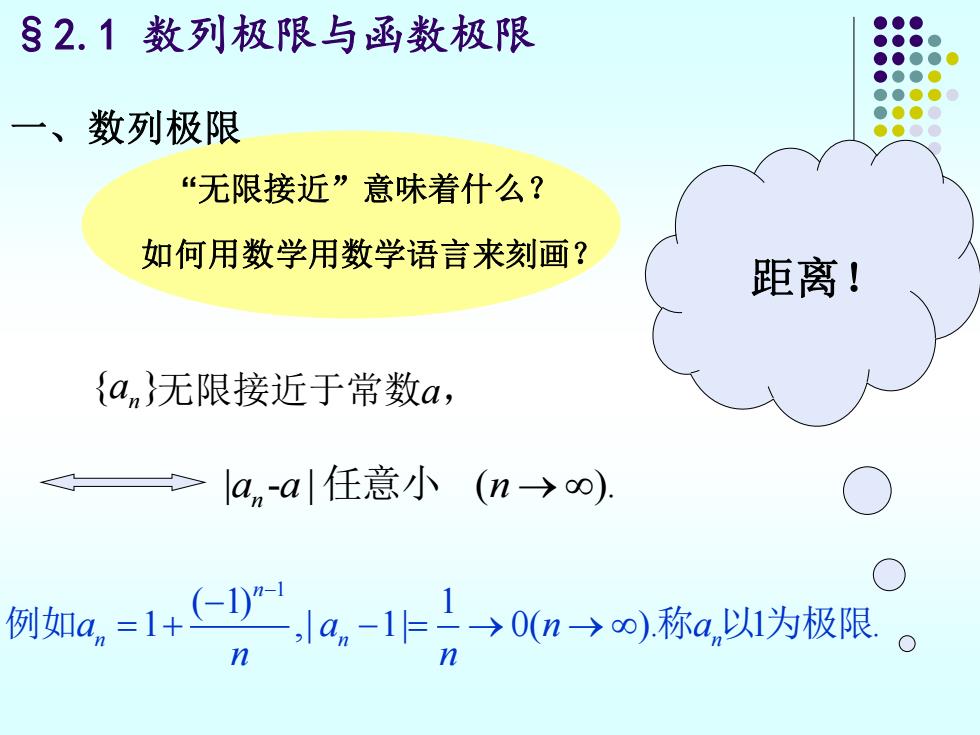
一、数列极限 “无限接近”意味着什么? 如何用数学用数学语言来刻画? 距离! { } an 无限接近于常数a, | - | ( ). n a a n 任意小 → 1 ( 1) 1 1 ,| 1| 0( ). 1 . n n n n a a n a n n − − 例如 = + − = → → 称 以 为极限 §2.1 数列极限与函数极限