西安电子科技大学：《实用大众线性代数》课程PPT教学课件（MATLAB版）第6章 线性代数其他领域应用

程序pla603核心语句 G1=200;G2=100;L1=2;L2=sqt(2);%给原始参数赋值 theta1 =pi/6;theta2 =pi/4; %将度化为弧度 %则按此次序，系数矩阵A,B可写成下式 A=[1,0,0,0,1,0;0,1,0,0,0,1;0,0,0,0,-sin(theta1),cos(theta1); 0,0,1,0,-1,0;0,0,0,1,0,-1;0,0,0,0,sin(theta2),cos(theta2)] B=[0;G1;G1/2*cos(theta1);0;G2;-G2/2*cos(theta2)]; X=AIB %用左除求解线性方程组 程序运行结果： 「1000 1.0000 0 0 95.0962 0100 0 1.0000 200.0000 154.9038 0000 -0.5000 0.8660 86.6025 -95.0962 A= B= 0010 ,X= -1.0000 0 0 145.0962 0001 0 -1.0000 100.0000 -95.0962 0 000 0.7071 0.7071 -35.3553 45.0962

程序pla603核心语句 G1=200; G2=100; L1= 2; L2 = sqrt(2) ; % 给原始参数赋值 theta1 =pi/6; theta2 =pi/4; % 将度化为弧度 % 则按此次序，系数矩阵A,B可写成下式 A=[1,0,0,0,1,0;0,1,0,0,0,1;0,0,0,0,-sin(theta1), cos(theta1);... 0,0,1,0,-1,0;0,0,0,1,0,-1;0,0,0,0, sin(theta2),cos(theta2)]; B=[0;G1;G1/2*cos(theta1);0;G2;-G2/2*cos(theta2)]; X = A\B % 用左除求解线性方程组 程序运行结果： 1 0 0 0 1.0000 0 0 95.0962 0 1 0 0 0 1.0000 200.0000 154.9038 0 0 0 0 0.5000 0.8660 86.6025 95.0962 , 0 0 1 0 1.0000 0 0 145.0962 0 0 0 1 0 1.0000 100.0000 95.0962 0 0 0 0 0.7071 0.7071 35.3553 4               − −   = = =     −       −   −             − A B X ， 5.0962                    

例6.4双滑块动力学方程 物体A(质量为m1)在具有斜面的物体 B(质量为m2)上靠重力下滑，设斜面 和地面均无摩擦力，求A沿斜面下滑 的相对加速度a1和B的加速度a2,并 求斜面和地面的支撑力N1及N2 ·解：分别画出A和B的受力图。 对物体A,B列写动力学方程，注意A 的绝对加速度是a1和a2的合成： 物体A x方向m,(acos0-a2)=N,sin0 (6.2.7) y方向m,a1sinB=m8-W1cos0 (6.2.8) 物体B x方向m,a2=N1sin0 (6.2.9) y方向N2-N1cos0-m28=0 (6.2.10)

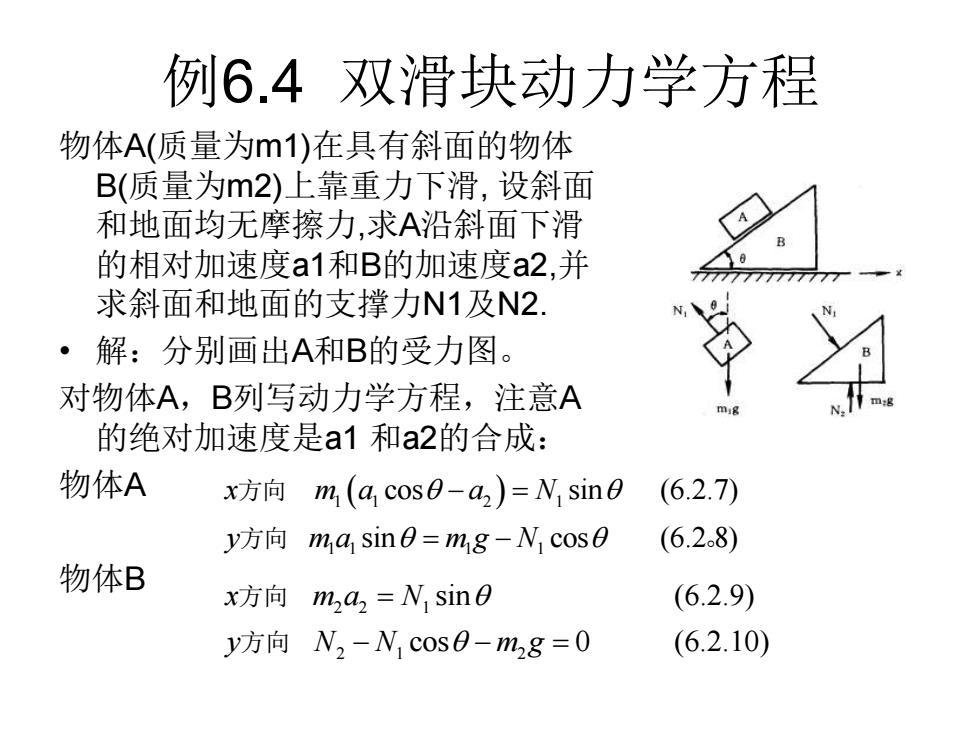
例6.4 双滑块动力学方程 物体A(质量为m1)在具有斜面的物体 B(质量为m2)上靠重力下滑, 设斜面 和地面均无摩擦力,求A沿斜面下滑 的相对加速度a1和B的加速度a2,并 求斜面和地面的支撑力N1及N2. • 解：分别画出A和B的受力图。 对物体A，B列写动力学方程，注意A 的绝对加速度是a1 和a2的合成： 物体A 物体B 1 1 2 1 ( ) 1 1 1 1 cos sin (6.2.7) sin cos (6.2 8) x m a a N y m a m g N     − = = − 方向 方向 。 2 2 1 2 1 2 sin (6.2.9) cos 0 (6.2.10) x m a N y N N m g   = − − = 方向 方向

双滑块动力学方程 ·矩阵方程为： m cose-m -sine 07 a 0 m sin O 0 cos0 0 2 mg →AX=B 0 m -sin0 0 0 0 -cos0 1N2 m28 ·程序pla604核心语句如下： A=m1*cos(theta),-m1,-sin(theta),0;m1*sin(theta),0,cos(theta),0;... 0,m2,-sin(theta),0;0,0,-cos(theta),1 ] B=[0,m1*g,0,m2*g';X=AB; ·运行结果： 输入m1=2,m2=4,及theta=30,得到 a1=6.54;a2=1.89,N1=15.10;N2=52.32

双滑块动力学方程 • 矩阵方程为： • 程序pla604核心语句如下： A = [ m1*cos(theta),-m1, -sin(theta), 0;m1*sin(theta), 0, cos(theta), 0;... 0 , m2, -sin(theta), 0; 0, 0, -cos(theta), 1 ]; B = [ 0, m1*g, 0, m2*g]'; X=A\B; • 运行结果： 输入m1=2,m2=4,及theta=30,得到 a1 = 6.54; a2 = 1.89，N1 = 15.10; N2 = 52.32 1 1 1 1 2 1 2 1 2 2 cos sin 0 0 sin 0 cos 0 0 sin 0 0 0 0 cos 1 m m a m a m g m N N m g         − −             =      −            −     AX = B

6.3信号与系统中的应用 信号流图的基本概念： 信号流图是用来表示和分析复杂 系统内的信号变换关系的工具。 它和交通流图或其他的物流图不 同，其基本概念如下： (1)系统中每个信号用图上的 一个节点表示，如图中的u,X1,2。 (2)系统部件对信号实施的变换关系用有向线段表示，箭 尾为输入信号，箭头为输出信号，箭身标注对此信号进行 变换的乘子。如图中的G1和G2。如果乘子为1，可以不必 标注。 (3)每个节点信号的值等于所有指向此节点的箭头信号之 和，每个节点信号可以向外输出给多个节点，其值都等于 节点信号

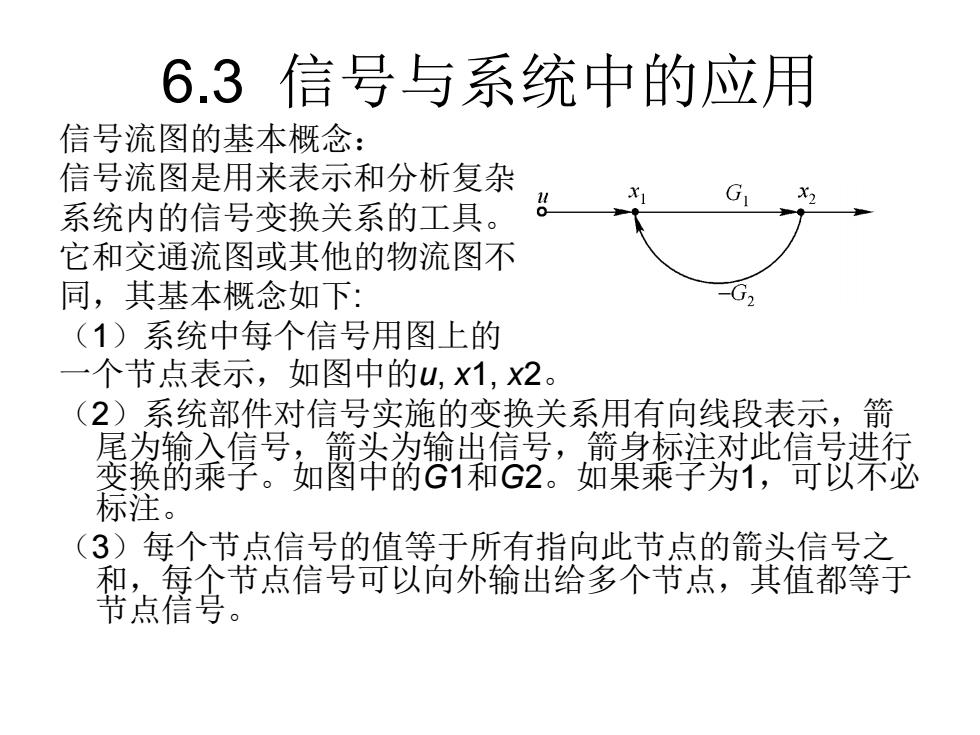
6.3 信号与系统中的应用 信号流图的基本概念： 信号流图是用来表示和分析复杂 系统内的信号变换关系的工具。 它和交通流图或其他的物流图不 同，其基本概念如下: （1）系统中每个信号用图上的 一个节点表示，如图中的u, x1, x2。 （2）系统部件对信号实施的变换关系用有向线段表示，箭 尾为输入信号，箭头为输出信号，箭身标注对此信号进行 变换的乘子。如图中的G1和G2。如果乘子为1，可以不必 标注。 （3）每个节点信号的值等于所有指向此节点的箭头信号之 和，每个节点信号可以向外输出给多个节点，其值都等于 节点信号

例6.5信号流图模型和梅森公式 上图可以表示为节点x1和x2处的两个方程 X1=-G2x2+u x2=GX1 x1_「0-G27x1.1 写成矩阵方程为x」G0十0 或 x=Qx+Pu 移项整理后，可以得到求未知信号向量x的公式， x=(I-Q)-1Pu 定义传递函数W为输出信号与输入信号之比xu,则有 W=x/u=(I-Q)-1P 因为 故：

例6.5 信号流图模型和梅森公式 上图可以表示为节点x1和x2处的两个方程 。 写成矩阵方程为 或 x = Qx + Pu 移项整理后，可以得到求未知信号向量x的公式， x = ( I - Q ) -1Pu 定义传递函数W为输出信号与输入信号之比x/u，则有 W = x/u = ( I - Q ) -1P 因为 故： 1 2 2 1 2 1 x G x u + x G x = − = 1 2 1 2 1 2 0 1 0 0 x G x u x G x       −         = +           1 2 2 1 1 1 2 1 1 1 1 1 1 G G G G G G −     − = =         − + -1 (I - Q) 1 2 2 1 1 2 1 2 1 / 1 1 1 1 1 / 1 0 1 1 x u G x u G G G G G G     −         = =         + +     x / u =