西安电子科技大学：《实用大众线性代数》课程PPT教学课件（MATLAB版）第6章 线性代数其他领域应用

交流稳态电路的计算 将未知量Ua,Ub和l均移到等号左端，整理为矩阵方程，得 -0.5 0 Z i,→AX=BL Z, Z 0 Z 解题程序为pla602,将s代入，并用矩阵解出Ua,Ub,l1, 程序中变量都已是复数。程序运行结果显示Ub的实部和虚部， 也可用向量的幅值absUb和相角angleUb表示： Ub=-2.5000e+002-7.5000e+002i即Ub=-250-750i absUb=790.5694,angleUb=-108.4349

交流稳态电路的计算 将未知量Ua,Ub和I1均移到等号左端，整理为矩阵方程，得 解题程序为pla602，将Is代入，并用矩阵解出Ua,Ub,I1， 程序中变量都已是复数。程序运行结果显示Ub的实部和虚部， 也可用向量的幅值absUb和相角angleUb表示： Ub = -2.5000e+002 -7.5000e+002i 即Ub = -250 - 750 i absUb = 790.5694，angleUb = -108.4349 a 1 2 2 b 2 2 1 1 1 1 1 0 1 1 1 1 0.5 0 0 1 0 1 s L U Z Z Z U I Z Z Z I Z =   + −                     − − −                    −         AX = BIs

程序pla602.m核心语句 %设定元件参数 Z1=-j*250;Z2=250;ki=0.5;1s=2+j*0;zL=500+j*500; %设定系数矩阵A a11=1/Z1+1/Z2;a12=-1/Z2;a13=0; a21=-1/Z2;a22=1/Z2-1/zL;a23=-ki; a31=1/Z1;a32=0;a33=-1; %设定系数矩阵A,B A=[a11,a12,a13;a21,a22,a23;a31,a32,a33];B=[1;0;0]: X=A1B*1s;Ub=X(2)%求方程解X=[Ua;Ub;l1]及负载电压 %求负载电压的幅度和相角 absUb=abs(Ub),angleUb=angle(Ub)*180/pi

程序pla602.m核心语句 % 设定元件参数 Z1=-j*250; Z2=250; ki=0.5; Is=2+j*0; zL=500+j*500; % 设定系数矩阵A a11=1/Z1+1/Z2; a12=-1/Z2; a13=0; a21=-1/Z2; a22=1/Z2-1/zL; a23=-ki; a31=1/Z1; a32=0; a33=-1; % 设定系数矩阵A,B A=[a11,a12,a13; a21,a22,a23; a31,a32,a33]; B=[1;0;0]; X=A\B*Is;Ub=X(2) % 求方程解X=[Ua;Ub;I1]及负载电压 % 求负载电压的幅度和相角 absUb=abs(Ub), angleUb=angle(Ub)*180/pi

6.2力学中的应用 。 在力学中，静力学是一个代数问题，它研究物体 受力后的平衡方程。一个物体在平面上平衡，需 要两个方向力的平衡方程和一个力矩平衡方程。 空间物体的平衡需要三个坐标方向的力平衡和力 矩平衡，总共6个平衡方程。如果是几个物体相互 作用下的平衡，那么方程的总数就会成几倍的增 加。若用手工方法一个一个地去解联立方程，那 是非常麻烦的。 ·这些方程组通常都是线性的，所以可以归结为矩 阵方程求解。用线性代数方法可以避免解单个方 程和单个变量，只要把系数矩阵输入程序中，就 可同时得出所有的解

6.2 力学中的应用 • 在力学中，静力学是一个代数问题，它研究物体 受力后的平衡方程。一个物体在平面上平衡，需 要两个方向力的平衡方程和一个力矩平衡方程。 空间物体的平衡需要三个坐标方向的力平衡和力 矩平衡，总共6个平衡方程。如果是几个物体相互 作用下的平衡，那么方程的总数就会成几倍的增 加。若用手工方法一个一个地去解联立方程，那 是非常麻烦的。 • 这些方程组通常都是线性的，所以可以归结为矩 阵方程求解。用线性代数方法可以避免解单个方 程和单个变量，只要把系数矩阵输入程序中，就 可同时得出所有的解

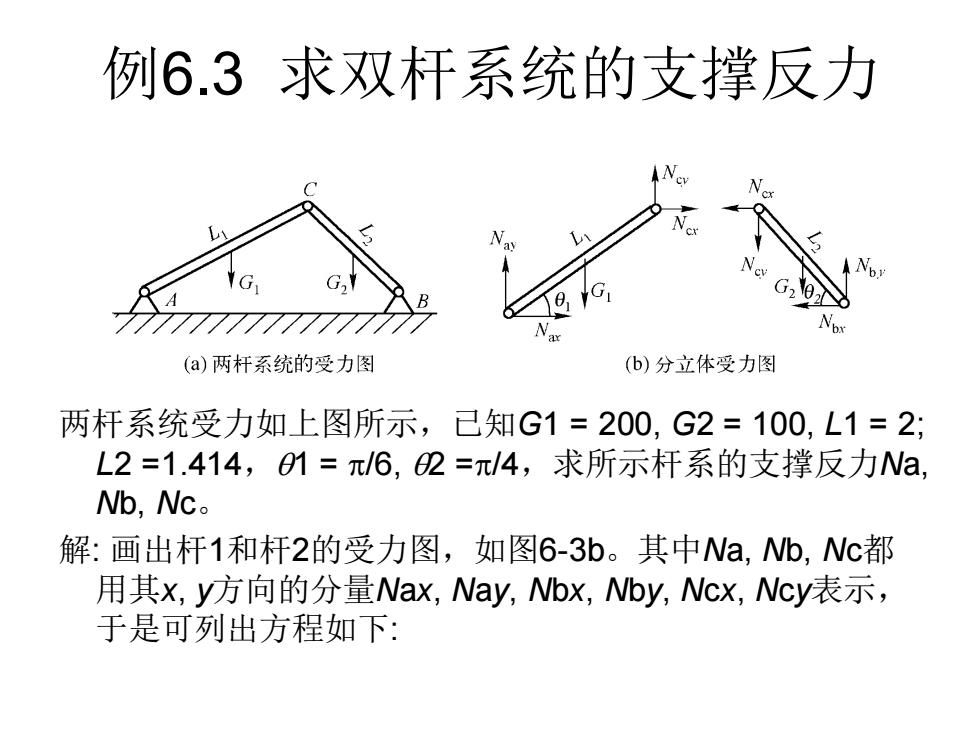
例6.3求双杆系统的支撑反力 (a)两杆系统的受力图 (b)分立体受力图 两杆系统受力如上图所示，已知G1=200,G2=100,L1=2; L2=1.414,01=π/6,2=π/4，求所示杆系的支撑反力Na, Nb,Nc. 解：画出杆1和杆2的受力图，如图6-3b。其中Na,Wb,Nc都 用其x,y方向的分量Nax,Way,Wbx,by,Wcx,Ncy表示， 于是可列出方程如下：

例6.3 求双杆系统的支撑反力 两杆系统受力如上图所示，已知G1 = 200, G2 = 100, L1 = 2; L2 =1.414，1 = /6, 2 =/4，求所示杆系的支撑反力Na, Nb, Nc。 解: 画出杆1和杆2的受力图，如图6-3b。其中Na, Nb, Nc都 用其x, y方向的分量Nax, Nay, Nbx, Nby, Ncx, Ncy表示， 于是可列出方程如下:

双杆系统的平衡方程 ·对杆件1： x方向力平衡： ∑X=0,Nax+Ncx=0(6.2.1) y方向力平衡： ∑Y=0,Nay+Ncy-G1=0(6.2.2) 绕A点力矩平衡：∑MA=O, NcyL1cosθ1-NcxL1sin01-G1L1/2c0sθ1=0 (6.2.3) ·对杆件2： X方向力平衡： ∑X=0,Wbx-Wcx=0 (6.2.4) y方向力平衡： ΣY=0,by-Ncy-G2=0(6.2.5) 绕B点力矩平衡：ΣMg=O, NcyL2cos02 NcxL2sin02+G2L2/2cos02 0 (6.2.6)

双杆系统的平衡方程 • 对杆件1: x方向力平衡： ΣX = 0, Nax + Ncx = 0 (6.2.1) y方向力平衡： ΣY = 0, Nay + Ncy - G1 = 0 (6.2.2) 绕A点力矩平衡：ΣMA = 0, NcyL1cos1-NcxL1sin1-G1L1/2cos1 = 0 (6.2.3) • 对杆件2: x方向力平衡： ΣX = 0, Nbx - Ncx = 0 (6.2.4) y方向力平衡： ΣY = 0, Nby - Ncy - G2 = 0 (6.2.5) 绕B点力矩平衡：ΣMB = 0, NcyL2cos2 + NcxL2sin2+G2L2/2cos2 = 0 (6.2.6)