
第三章 序列的两种傅立叶变换 1
1 第三章 序列的两种傅立叶变换

序列的两种傅立叶变换 ·3.1序列信号的周期性和频率 ·3.2离散时间傅立叶变换(DTFT) ·3.3离散系统的频率特性 ·3.4周期序列的频谱一离散傅立叶级数 ·3.5离散傅立叶变换(DFT) 。3.6 DFT的特性 ·3.7用DT计算线性卷积 2
2 序列的两种傅立叶变换 • 3.1 序列信号的周期性和频率 • 3.2 离散时间傅立叶变换(DTFT) • 3.3 离散系统的频率特性 • 3.4 周期序列的频谱—离散傅立叶级数 • 3.5 离散傅立叶变换(DFT) • 3.6 DFT的特性 • 3.7 用DFT计算线性卷积

3.1序列信号的周期性和频率 ·连续信号的周期性:满足 x(t)=x(t+mp) m=0,±1,±2,… 的连续信号称为周期信号。其中最小的非零P值 称为信号的周期。 ·离散序列的周期性:对于序列x(n),若对所有 的n满足 x(n)=x(n+N) 称为周期序列,满足此式的最小值称为序列的 周期。 3
3 3.1 序列信号的周期性和频率 • 连续信号的周期性:满足 的连续信号称为周期信号。其中最小的非零P值 称为信号的周期。 • 离散序列的周期性:对于序列x(n),若对所有 的n满足 称为周期序列,满足此式的最小值N称为序列的 周期。 x(t) = x(t + mP) m = 0, 1, 2, x(n) = x(n + N)

连续信号的正负频率 连续余弦信号的频率成分:化为指数形式 c0s21-长+e) 因此它由正负两个频率成分组成。其几何意义可 以从运行g即312演示程序看出。 对正弦信号 j-sinf=)k-ey) 也可作类似的分析。也由正负两个频率成分组成
4 连续信号的正负频率 连续余弦信号的频率成分:化为指数形式 因此它由正负两个频率成分组成。其几何意义可 以从运行fgp312演示程序看出。 对正弦信号 也可作类似的分析。也由正负两个频率成分组成。 ( ) j t j t t e e 0 0 2 1 cos 0 − = + ( ) j t j t j t e e 0 0 2 1 sin 0 − = −
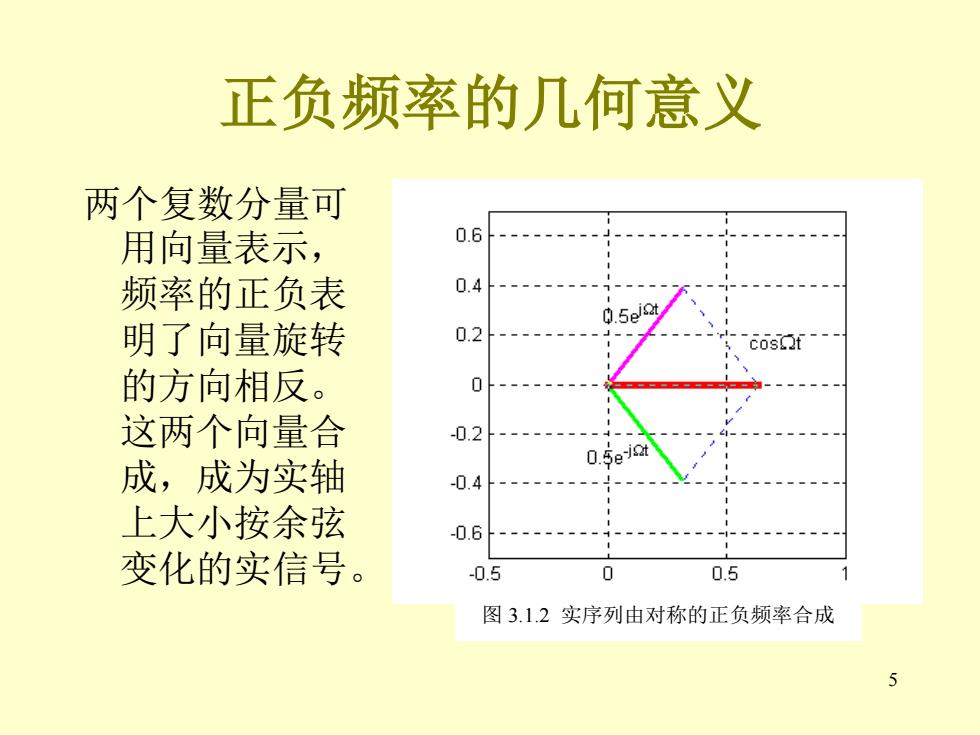
正负频率的几何意义 两个复数分量可 用向量表示, 0.6 频率的正负表 0.4 明了向量旋转 0.2 cos.t 的方向相反。 0 这两个向量合 -0.2 成,成为实轴 0.5e2t -04--------}-- 上大小按余弦 -0.6 变化的实信号。 -0.5 0 0.5 图3.1.2实序列由对称的正负频率合成 5
5 正负频率的几何意义 两个复数分量可 用向量表示, 频率的正负表 明了向量旋转 的方向相反。 这两个向量合 成,成为实轴 上大小按余弦 变化的实信号。 图 3.1.2 实序列由对称的正负频率合成