
二、空间直角坐标系中两点间的距离公式及中点坐标公式 【问题思考】 1.在空间直角坐标系Oyz下,若点A(2,2,2),B(4,-6,-2),点P是线 段AB的中点,则A,B之间的距离是多少?点P的坐标是什么? 提示:AB=0B-0A=(2,-8,-4), ∴.AB=AB=V4+64+16=2V21. 0P=(0A+0B6,-4,0=3,-2,0, '.点P的坐标是(3,-2,0)
导航 二、空间直角坐标系中两点间的距离公式及中点坐标公式 【问题思考】 1.在空间直角坐标系Oxyz下,若点A(2,2,2),B(4,-6,-2),点P是线 段AB的中点,则A,B之间的距离是多少?点P的坐标是什么? 提示:∵𝑨 𝑩 = 𝑶 𝑩 − 𝑶 𝑨 =(2,-8,-4), ∴|AB|=|𝑨 𝑩 |= 𝟒 + 𝟔𝟒 + 𝟏𝟔=2 𝟐𝟏. ∵𝑶 𝑷 = 𝟏 𝟐 (𝑶 𝑨 + 𝑶 𝑩 )= 𝟏 𝟐 (6,-4,0)=(3,-2,0), ∴点 P 的坐标是(3,-2,0)

导航 2填空:若A心1y1,Z1),B(K2y22),点P是线段AB的中点,则有 (1)AB= (2)AB=AB= (3)P
导航 2.填空:若A(x1 ,y1 ,z1 ),B(x2 ,y2 ,z2 ),点P是线段AB的中点,则有 (1)𝑨 𝑩 = (x2-x1,y2-y1,z2-z1) . (2)AB=|𝑨 𝑩 |= (𝒙𝟐-𝒙𝟏) 𝟐 + (𝒚𝟐-𝒚𝟏) 𝟐 + (𝒛𝟐-𝒛𝟏) 𝟐 . (3)P 𝒙𝟏 +𝒙𝟐 𝟐 , 𝒚𝟏 +𝒚𝟐 𝟐 , 𝒛𝟏 +𝒛𝟐 𝟐

导期 3.做一做:已知点M(-1,2,0),N3,-4,6),求线段MN的中点P的坐 标和线段MN的长度! 解:P(1,-1,3); MWM=M=3-(12+(4-2)2+62= V16+36+36=2v22
导航 3.做一做:已知点M(-1,2,0),N(3,-4,6),求线段MN的中点P的坐 标和线段MN的长度. 解:P(1,-1,3); |MN|=|𝑴 𝑵 |= [𝟑-(-𝟏)] 𝟐 + (-𝟒-𝟐) 𝟐 + 𝟔𝟐 = 𝟏𝟔 + 𝟑𝟔 + 𝟑𝟔=2 𝟐𝟐

导航 【思考辨析】 判断正误(正确的画“√,错误的画“X) (1)同一点在不同的空间直角坐标系下的坐标不同.( (2)点1,1,-1)在第皿卦限.( 3)点M1,2,3)到点N(-1,-2,-3)的距离是2V14.() (4)对于线段MN及其中点P,已知点M,P的坐标,就能求得点N 的坐标()
导航 【思考辨析】 判断正误.(正确的画“ ”,错误的画“×”) (1)同一点在不同的空间直角坐标系下的坐标不同.( ) (2)点(1,1,-1)在第Ⅷ卦限.( × ) (3)点M(1,2,3)到点N(-1,-2,-3)的距离是 .( ) (4)对于线段MN及其中点P,已知点M,P的坐标,就能求得点N 的坐标.( ) 2 𝟏𝟒
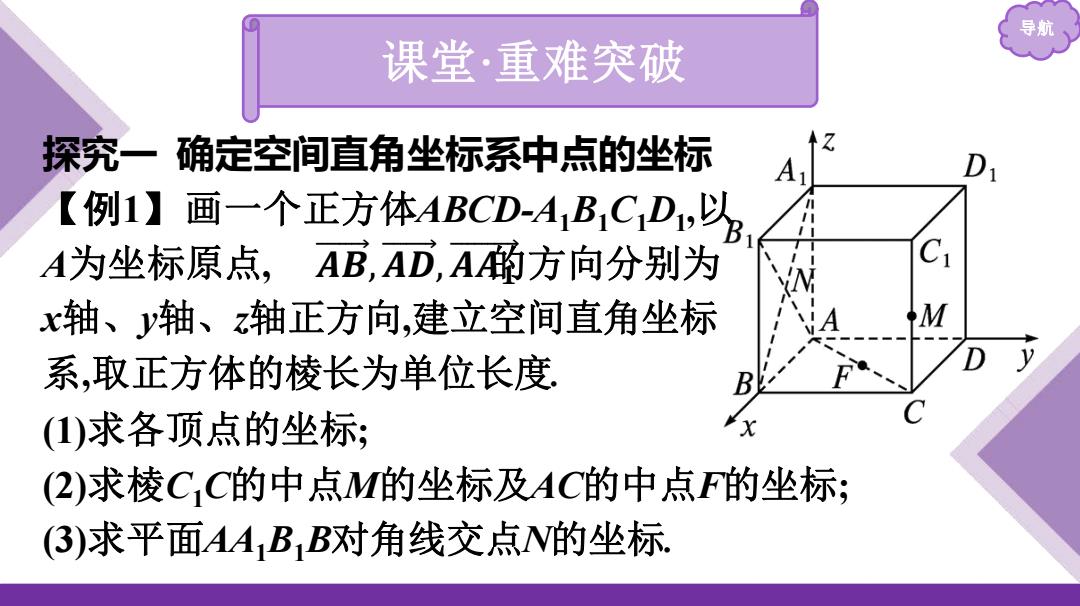
导期 课堂·重难突破 探究一确定空间直角坐标系中点的坐标 A 【例1】画一个正方体ABCD-AB,CD,以 A为坐标原点,AB,AD,A的方向分别为 x轴、轴、z轴正方向,建立空间直角坐标 系,取正方体的棱长为单位长度 (1)求各顶点的坐标; (2)求棱C,C的中点M的坐标及AC的中点F的坐标; (3)求平面AABB对角线交点N的坐标
导航 课堂·重难突破 探究一 确定空间直角坐标系中点的坐标 【例1】画一个正方体ABCD-A1B1C1D1 ,以 A为坐标原点, 的方向分别为 x轴、y轴、z轴正方向,建立空间直角坐标 系,取正方体的棱长为单位长度. (1)求各顶点的坐标; (2)求棱C1C的中点M的坐标及AC的中点F的坐标; (3)求平面AA1B1B对角线交点N的坐标. 𝑨 𝑩 ,𝑨 𝑫 ,𝑨𝑨𝟏