
2、存在定理(仅给出内容,不做证明) 定理1 当函数f(x)在区间a,b上连续时, 则f(x)在区间a,b]上可积 定理2 设函数f(x)在区间a,b]上有界, 且只有有限个间断点, 则f(x)在 区间a,b]上可积. 2012329 素山医学院信息工程学院高等数学教研室

3、定积分的几何意义 f(x)>0,f(x)=A 曲边梯形的面积 f(x)<0,f(x)=-A曲边梯形的面积的负值 [f(x)dx=A-A +A-A 2012.329 素山医学院信息工程学院高等数学教研室
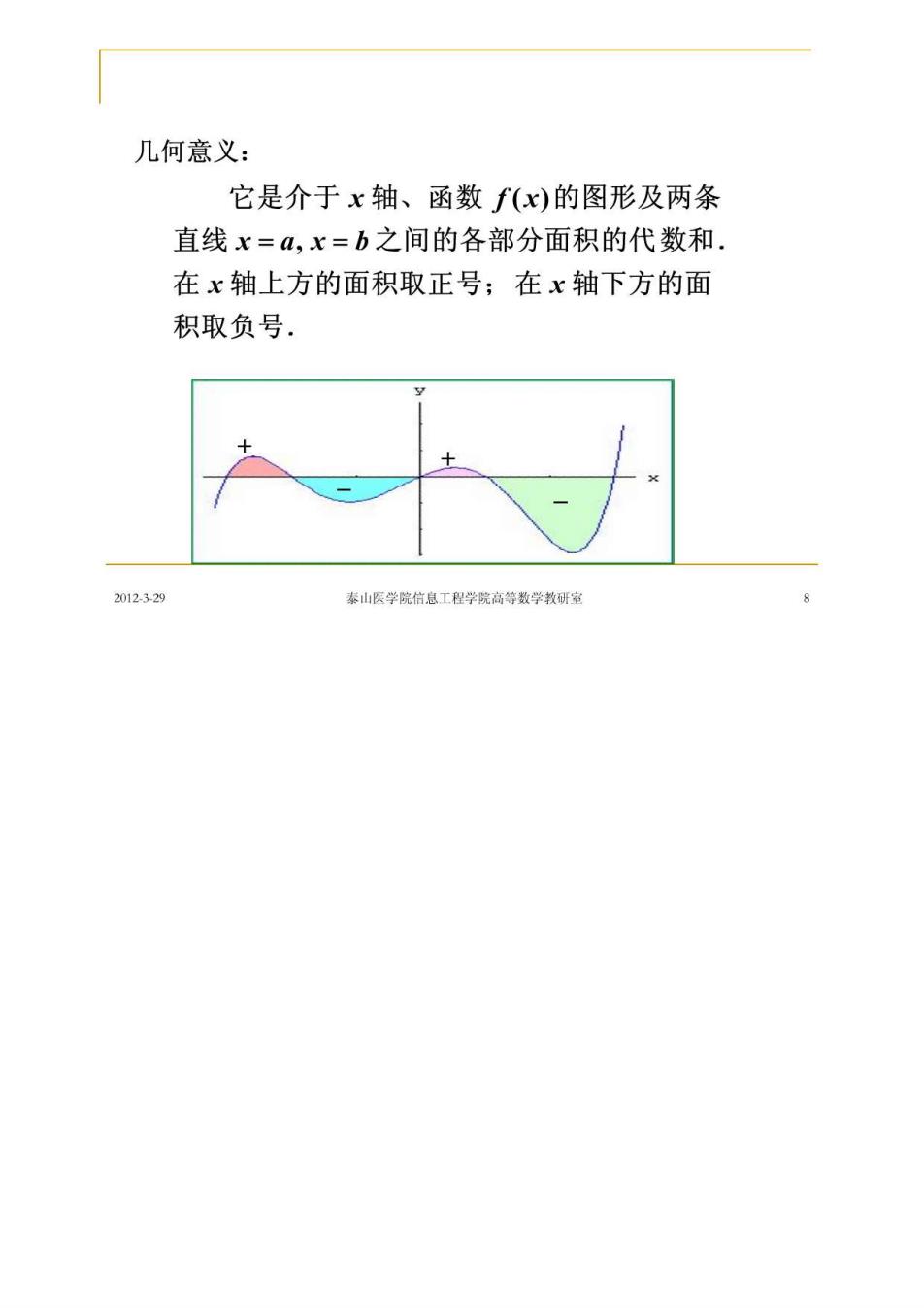
几何意义: 它是介于x轴、函数f(x)的图形及两条 直线x=4,x=b之间的各部分面积的代数和 在x轴上方的面积取正号;在x轴下方的面 积取负号 X 2012329 素山医学院信息工程学院高等数学教研室

定积分的性质 对定积分的补充规定 (1)当a=b时, Ff(x)dx=0: (2)当a>b时, 心fx)s=-Sf(x)d 说明在下面的性质中,假定定积分都存在,且不 考虑积分上下限的大小. 2012329 泰山医学院信息工程学院高等数学教研室

性质1 f(x)±g(xdc=f(x)dc±g(x)d. (此性质可以推广到有限多个函数作和的情况) 性质2心付(x)=kf(x)d本(k为任意常数) 性质3假设a<c<b f(x)dx=[f(x)dx+f(x)dx. 补充:不论a,b,c的相对位置如何,上式总成立. (定积分对于积分区间具有可加性) 2012329 泰山医学院信息工程学院高等数学教研室