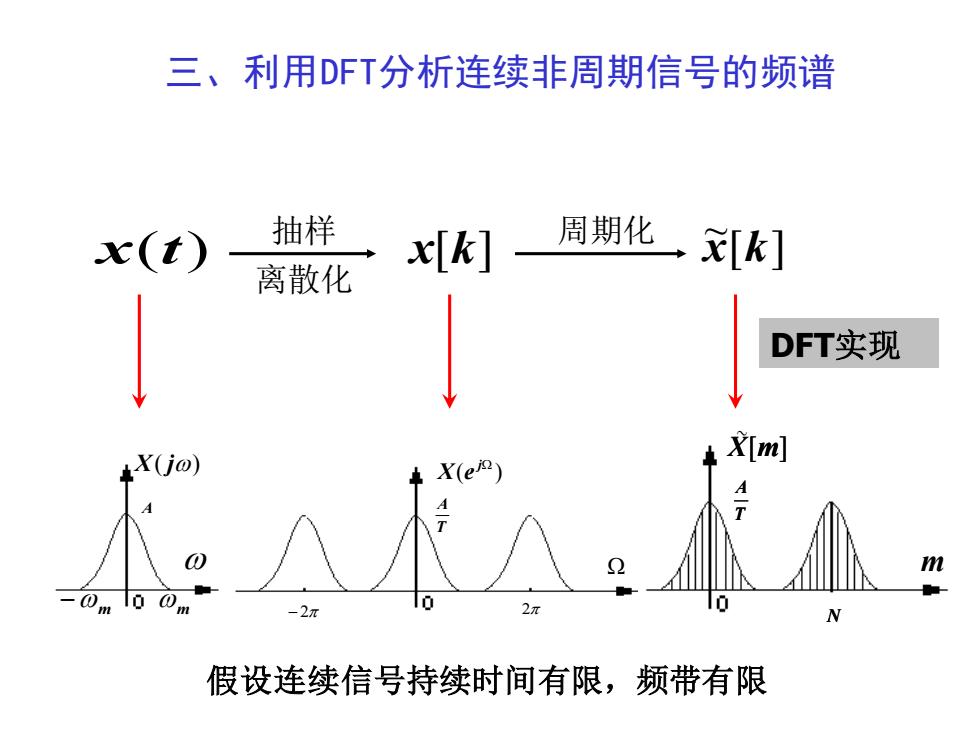
三、利用DFT分析连续非周期信号的频谱抽样周期化、x[k]x[k]x(t)离散化DFT实现X[m]AT0m2To0①m@102元2-2元N频带有限假设连续信号持续时间有限
x(t) 抽样 离散化 x[k] 周期化 [ ] ~ x k X( j) − m m A ( ) j X e − 2 2 T A m N X[m] T A m N X[m] T A N X[m] T A ~ 三、利用DFT分析连续非周期信号的频谱 DFT实现 假设连续信号持续时间有限,频带有限
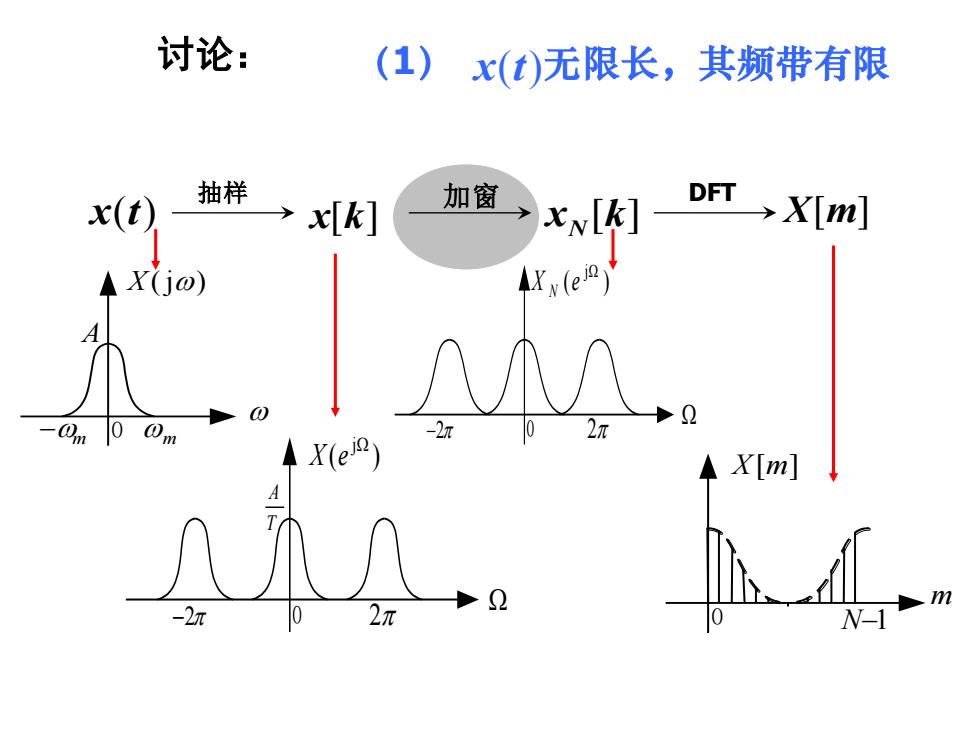
讨论:(1)x(t)无限长,其频带有限抽样DFT加窗X[m]X[k]x[k]A X(j)202元0-2元0m0X[m]m2元0-2元0N-1
讨论: (1) x(t) 无限长,其频带有限 x[k] X[m] 加窗 −2 2 ( ) j X e N 0 −2 2 ( ) j X e 0 T A −m X (j) 0 A m m X[m] 0 N−1 x(t) 抽样 x [k] N DFT
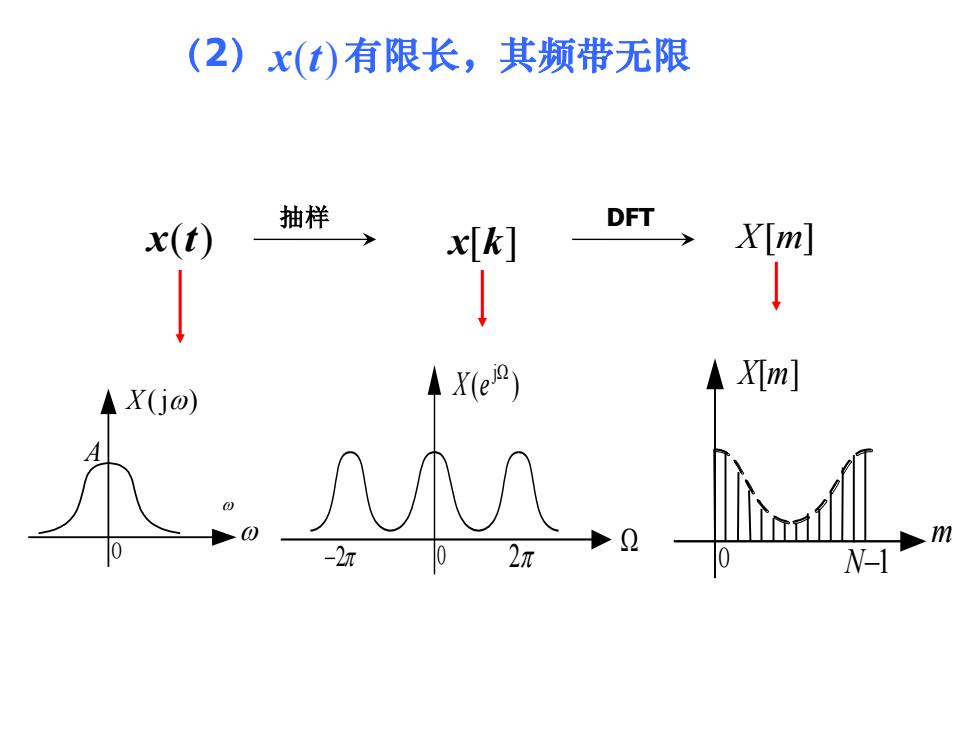
(2)x(t)有限长,其频带无限抽样DFTX[m]x(t)x[k]X[m]X(jo)mQ02元0-2元0N-1
(2) x(t) 有限长,其频带无限 X (j) 0 A −2 2 ( ) j X e 0 m X[m] 0 N−1 x(t) 抽样 x[k] X[m] DFT
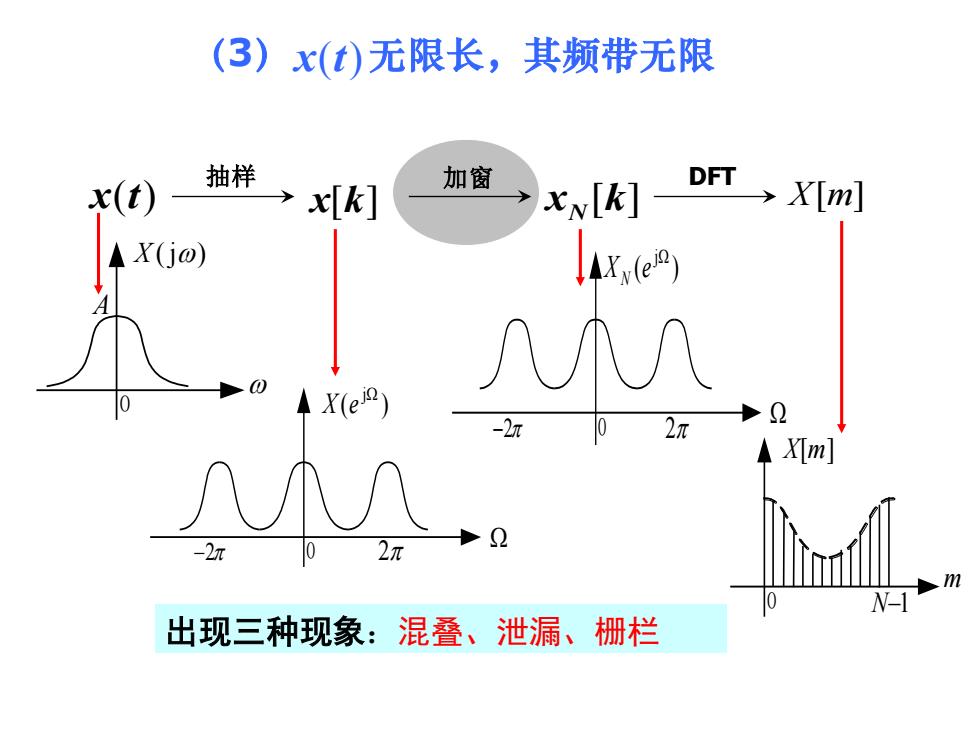
(3)x(t)无限长,其频带无限抽样加窗DFT> X[m]X[k]x[k]X(io)ATX?2元-2元0X[m]Q2元-2元JOmN-10混叠、泄漏、栅栏出现三种现象:
(3) x(t) 无限长,其频带无限 x [k] N 加窗 出现三种现象:混叠、泄漏、栅栏 X (j) 0 A −2 2 ( ) j X e 0 −2 2 ( ) j X e N 0 m X[m] 0 N−1 x(t) x[k] 抽样 X[m] DFT
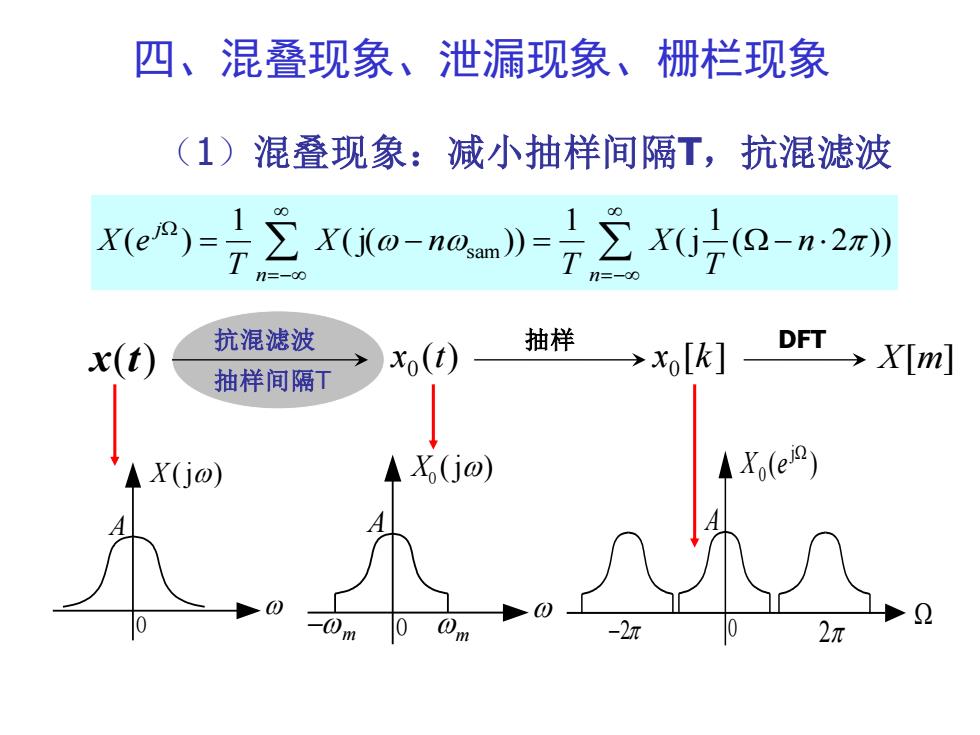
四、混叠现象、泄漏现象、栅栏现象(1)混叠现象:减小抽样间隔T,抗混滤波X(e1)=2X(i(α-n0am)=≥ X(i_(Q-n·2元)-80o抽样抗混滤波DFTxo(t)>xo[k]x(t)> X[m]抽样间隔TA X(jo)XjoAQ000m102元-2元m
四、混叠现象、泄漏现象、栅栏现象 (1)混叠现象:减小抽样间隔T,抗混滤波 X (j) 0 A 0 A −2 2 ( ) j 0 X e X (j) 0 A 0 − m m x(t) 抗混滤波 抽样间隔T ( 2 )) 1 (j 1 (j( )) 1 ( ) = − sam = − =− =− n T X T X n T X e n n j ( ) 0 x t 抽样 [ ] 0 x k X[m] DFT