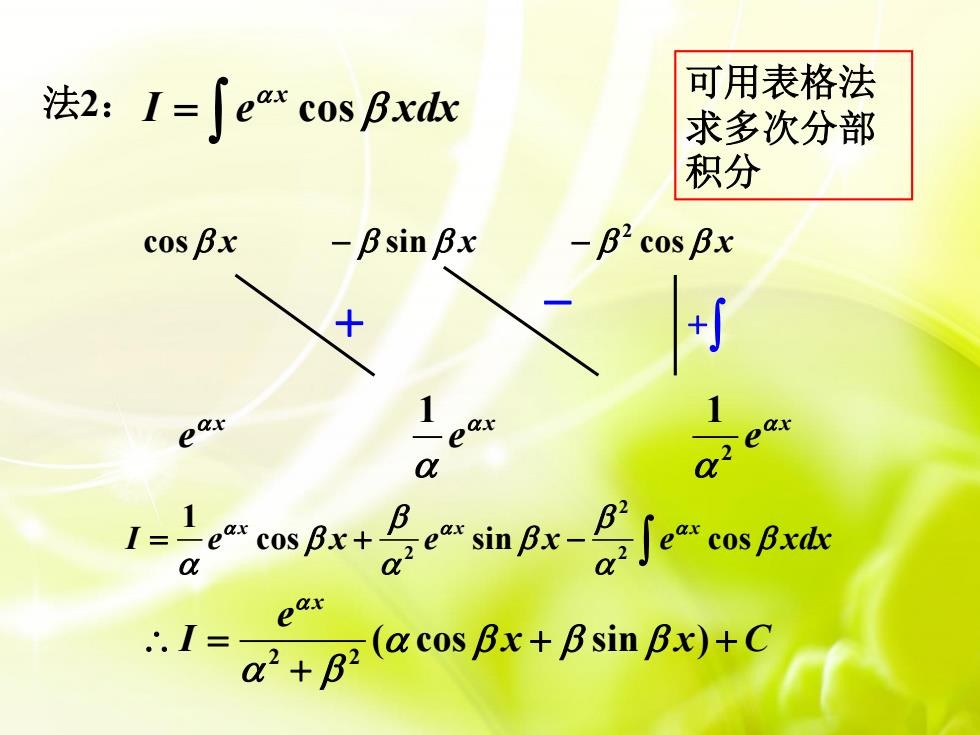
可用表格法法2: I =[eax cos βxdx求多次分部积分-βcos βxcosβx-βsin βx+[+1axeeraxe2QαβReaxeateaxcosβxdxcos βx+sinBxQ2αeer(α cos βx + βsin βx)+Cα?+β2
可用表格法 求多次分部 积分 cos x I e xdx = 2 cos sin cos x x x − − 2 1 1 x x x e e e + − + 2 2 2 1 cos sin cos x x x I e x e x e xdx = + − 2 2 ( cos sin ) x e I x x C = + + + 法2 :

练习[x(lnx)* dx.解:令u=lnx,则x =e",dx=e"du原式- [e3"-u".e" du =[u'e4" du44u3012u?24u24I-[++十4u4u14u14u14u4u1ee114e45eAee4333324u原式+C-uVAu+一32--184333-+(n*x-*+1+C一InInx+x-一8324
3 4 x x x (ln ) d . 练习 ln , , d d u u 解:令u x x e x e u = = = 则 3 4 d u u = e u e u 原式 4 4 d u = u e u 4 u 4u e 3 4u 2 12u 24u 24 0 1 4 4 u e 2 1 4 4 u e 3 1 4 4 u e 4 1 4 4 u e 5 1 4 4 u e + − + − + ( ) 1 3 3 3 4 4 3 2 4 4 8 32 u 原式 = − + − + + e u u u u C ( ) 1 3 3 3 4 4 3 2 ln ln ln ln 4 4 8 32 = − + − + + x x x x x C −

例6求xtan’xdx解J x tan’ xdx = J x(sec’ x-1)dx=J xsec’ xdx-{ xdx-[ xdtanx-{ xdx= xtanx-[ tanxdx-[xdx=xtan +Imlo -→+C>说明:有时在用分部积分之前,须先变形
例6 求 x tan xdx 2 解 x tan xdx x(sec x 1)dx 2 2 = − = xsec xdx − xdx 2 = xdtan x − xdx = x tan x − tan xdx − xdx C x = x x + x − + 2 tan ln cos 2 ➢说明:有时在用分部积分之前, 须先变形

例7secxdxsec"xdx解= [ sec xd tan x= sec x tan x - [ tan’ x sec xdx= sec x tan x+ [ sec xdx -[ sec' xdxsecxdx= sec x tan x + In sec x + tan x-1→ sec' xdx == sec x tan x+=ln(sec x+tanx)+C22
例 7 3 sec xdx 解 3 sec xdx = sec tan xd x 2 = − sec tan tan sec x x x xdx 3 = + − sec tan sec sec x x xdx xdx 3 = + + − sec tan ln sec tan sec x x x x xdx 3 1 1 sec sec tan ln(sec tan ) 2 2 = + + + xdx x x x x C

[ (2x? -1)e-* dxe*(1 + sin x)Cdx1+ cos x
2 2 (2 1) x x e dx − − (1 sin ) 1 cos x e x dx x + +