第9章图论 定义9.1.2若图G有n个结点,则称该图为n阶图。 定义9.1.3设G为图,如果G的所有边都是有向边,则 称G为有向图。如果G的所有边都是无向边,则称G为无向 图。如果G中既有有向边,又有无向边,则称G为混合图。 图9.3的(a)是无向图,(b)是有向图,(c是混合图。 OVs V2 (a) (b) (c) 图9.3
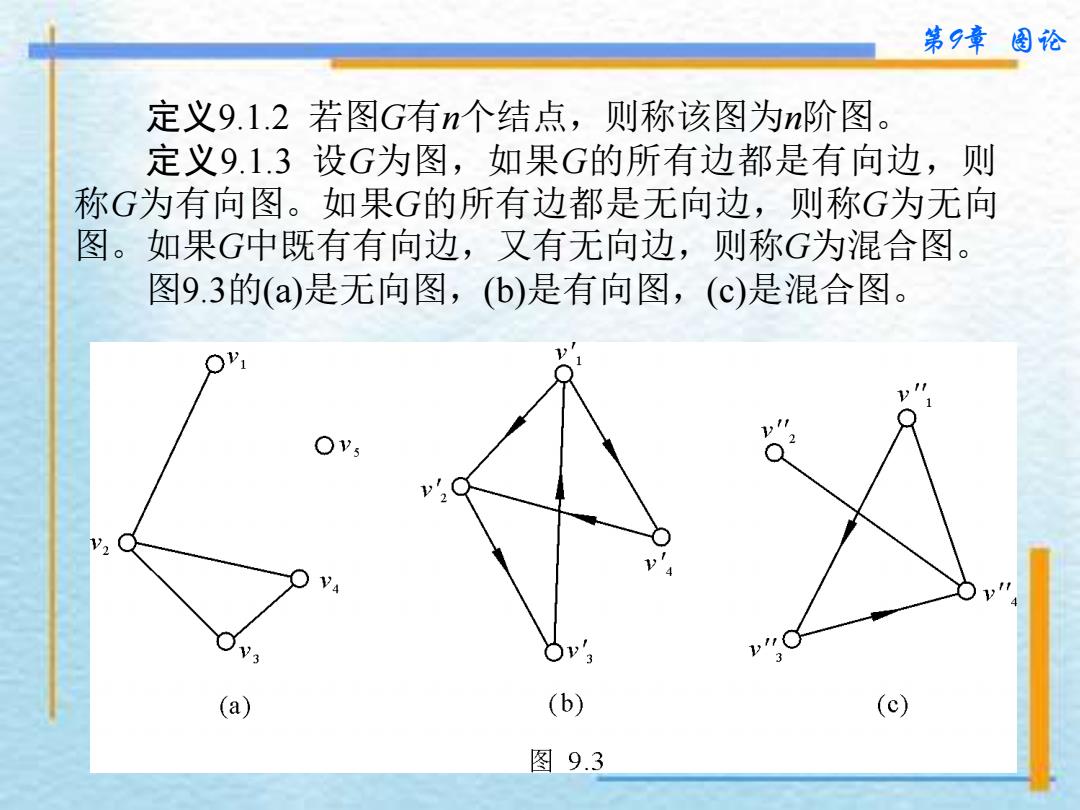
第9章 图论 定义9.1.2 若图G有n个结点,则称该图为n阶图。 定义9.1.3 设G为图,如果G的所有边都是有向边,则 称G为有向图。如果G的所有边都是无向边,则称G为无向 图。如果G中既有有向边,又有无向边,则称G为混合图。 图9.3的(a)是无向图,(b)是有向图,(c)是混合图

第9章图论 在一个图中,若两个结点由一条边(有向边或无向边) 关联,则称其中的一个结点是另一个结点的邻接点。并 称这两个结点相互邻接。 在一个图中不与任何结点相邻接的结点,称为孤立 点。 在一个图中,如果两条边关联于同一个结点,则称 其中的一个边是另一个边的邻接边。并称这两个边相互 邻接。关联于同一个结点的一条边叫做环或自回路。在 有向图中环的方向可以是顺时针,也可以是逆时针,它 们是等效的。 定义9.1.4 由孤立点组成的图叫做零图。由一个孤立 点组成的图叫做平凡图。 根据定义9.1.4,平凡图一定是零图
第9章 图论 在一个图中,若两个结点由一条边(有向边或无向边) 关联,则称其中的一个结点是另一个结点的邻接点。并 称这两个结点相互邻接。 在一个图中不与任何结点相邻接的结点,称为孤立 点。 在一个图中,如果两条边关联于同一个结点,则称 其中的一个边是另一个边的邻接边。并称这两个边相互 邻接。关联于同一个结点的一条边叫做环或自回路。在 有向图中环的方向可以是顺时针,也可以是逆时针,它 们是等效的。 定义9.1.4 由孤立点组成的图叫做零图。由一个孤立 点组成的图叫做平凡图。 根据定义9.1.4,平凡图一定是零图

第9章图论 9.1.2结点的度及其性质 定义9.1.5设G=<V,E>是图,veV,与v相关联的边数 叫做结点v的度。记为deg(v)。规定,自回路为所在结点 增加2度。 在图G=<V,E>中,度数最大(小)的结点的度叫做图G 的最大(小)度,记为△(G)(⑧(G)。图G的最大度和最小度 表示为: A(G)=maxi deg(v)ve δ(G)=min deg(v)|veVY 在图9.1中,△(G)=4,δ(G)=0
第9章 图论 9.1.2结点的度及其性质 定义9.1.5 设G=V,E是图,vV,与v相关联的边数 叫做结点v的度。记为deg(v)。规定,自回路为所在结点 增加2度。 在图G=V,E中,度数最大(小)的结点的度叫做图G 的最大(小)度,记为(G)((G))。图G的最大度和最小度 表示为: (G)=max deg(v) | vV (G)= min deg(v) | vV 在图9.1中, (G)=4,(G)=0

第9章图论 定理9.1.1在任何图G=<V,E>中,所有结点度数的和 等于边数的2倍。即: ∑deg(v)=2El v∈V 证明:图的每一条边都和两个结点相关联,为每个 相关联的结点增加一度,给图增加两度。所以所有结点度 数的和等于边数的2倍。 推论在任何图G=<V,E>中,度数为奇数的结点必为 偶数个
第9章 图论 定理9.1.1 在任何图G=V,E中,所有结点度数的和 等于边数的2倍。即: = 2|E| 证明:图的每一条边都和两个结点相关联,为每个 相关联的结点增加一度, 给图增加两度。所以所有结点度 数的和等于边数的2倍。 推论 在任何图G=V,E中,度数为奇数的结点必为 偶数个。 vV deg(v)

第9章图论 定义9.1.6设G=<V,E>是有向图,veV,射入(出)结点 v的边数称为结点v的入(出)度。记为deg(v)(deg+(v)。 显然,任何结点的入度与出度的和等于该结点的度数, deg(v)=deg(v)+deg(v). 定理9.1.2在有向图中,所有结点入度的和等于所有 结点出度的和。 证明:在有向图中每一条边对应一个入度和一个出 度,为图的入度和出度各增加1。所以,所有结点入度的 和等于边数,所有结点出度的和也等于边数
第9章 图论 定义9.1.6 设G=V,E是有向图,vV,射入(出)结点 v的边数称为结点v的入(出)度。记为deg-(v) (deg+(v))。 显然,任何结点的入度与出度的和等于该结点的度数, 即deg(v)=deg-(v)+deg+(v)。 定理9.1.2 在有向图中,所有结点入度的和等于所有 结点出度的和。 证明:在有向图中每一条边对应一个入度和一个出 度,为图的入度和出度各增加1。所以,所有结点入度的 和等于边数,所有结点出度的和也等于边数