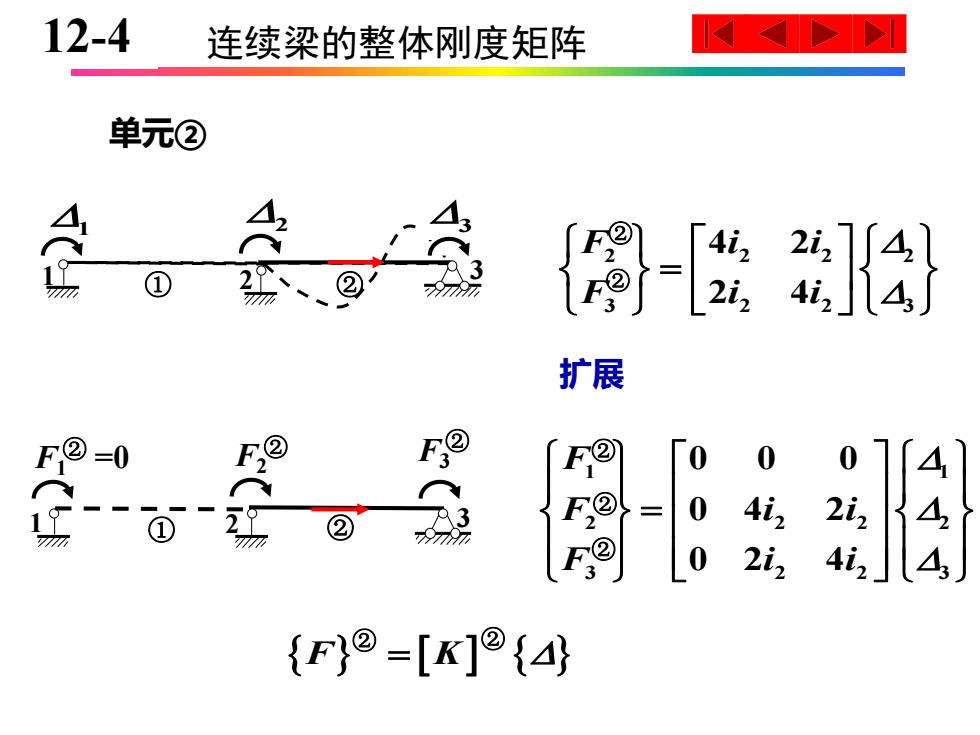
12-4 连续梁的整体刚度矩阵 ✉D> 单元② A A ∫F ② 扩展 =0 F 「F 0 0 0 ② F,®= 0 4 2 F 0 i2 444 {F}@=[K]@{A
10-4 连续梁的整体刚度矩阵 2 3 ② 1 2 ② 3 F1 =0 F2 1 ① 2 ② 1 3 单元② ② ① 2 2 2 2 3 3 2 2 4 2 2 4 F i i F i i = ② ② 扩展 F3 ② 1 1 2 2 2 2 3 2 2 3 0 0 0 0 4 2 0 2 4 F F i i F i i = ② ② ② F K = ② ② 128-4

12-4 连续梁的整体刚度矩阵 三个结点位移,需要用三个方程求解! F=F④+F②F=F+F, F=F+F® ① 2 ② {F}={FP+{Fy2-(]+[]②){A 结点力列向量一{F}=[K]{4}一结点位移列向量 整体刚度矩阵
10-4 连续梁的整体刚度矩阵 y x 三个结点位移,需要用三个方程求解! 1 2 3 ① 2 ② 1 3 F1=F1 +F1 ① ② F2=F2 +F2 ① ② F3=F3 +F3 ① ② F F F k k = + = + ( ) ① ② ① ② 结点力列向量 结点位移列向量 整体刚度矩阵 1 ① 2 ② 3 F K = 8-4 F K = 12

12-4 连续梁的整体刚度矩阵 4> [K]=[K]O+[K]② 展开 4i1 21 0 4i1 21 07 0 0 0 2i1 4i1+4i2 2i2 2i 4i1 0 + 0 4i2 2i2 0 2i, 0 0 0 0 2i2 4i2 单元①的 单元②的 换码重排座 贡献矩阵 贡献矩阵 按照单元定位向量由[求[
10-4 连续梁的整体刚度矩阵 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 4 2 4 2 2 4 2 4 4 2 4 2 2 4 2 4 i i i i i i i i i i i i i i i i + = + K K K = + ① ② 展开 单元①的 贡献矩阵 单元②的 换码重排座 贡献矩阵 按照单元定位向量由 [k] 求 e [K] 128-4
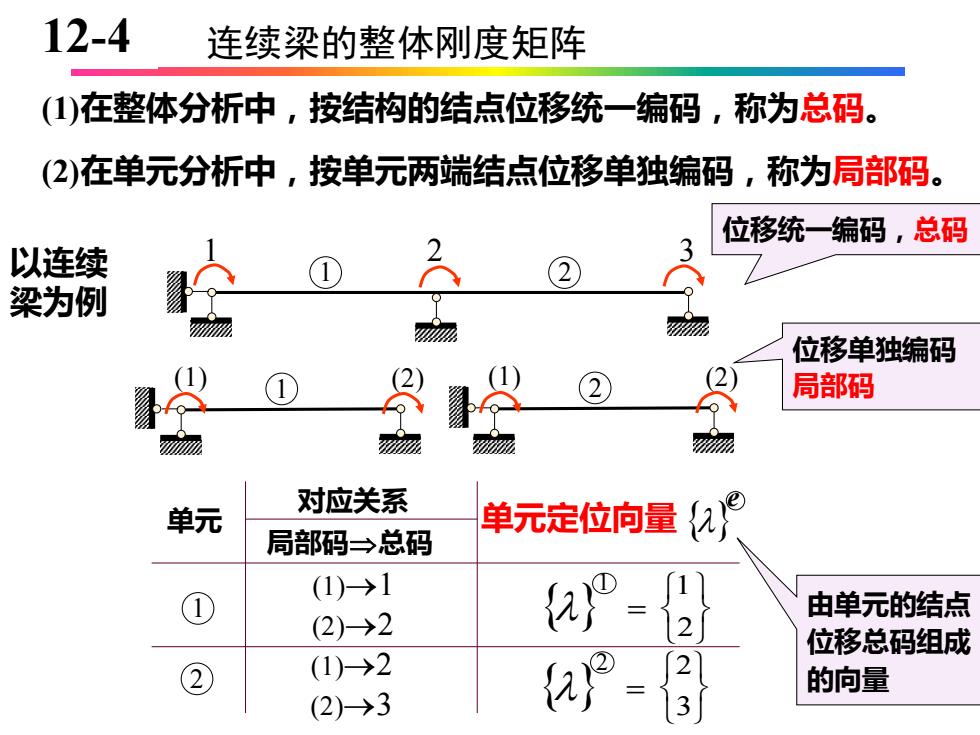
12-4 连续梁的整体刚度矩阵 (1)在整体分析中,按结构的结点位移统一编码,称为总码。 (2)在单元分析中,按单元两端结点位移单独编码,称为局部码。 位移统一编码,总码 以连续 2 梁为例 位移单独编码 局部码 流 单元 对应关系 单元定位向量{九 局部码→总码 (1)-→1 a”- 由单元的结点 (2)-→2 位移总码组成 ② (1)-→2 2 的向量 (2)-→3
10-4 连续梁的整体刚度矩阵 (1)在整体分析中,按结构的结点位移统一编码,称为总码。 (2)在单元分析中,按单元两端结点位移单独编码,称为局部码。 以连续 梁为例 1 2 1 2 3 1 (1) (2) 2 (1) (2) 位移统一编码,总码 单元 1 2 对应关系 局部码总码 单元定位向量 e (1)→1 (2)→2 1 = 2 1 (1)→2 (2)→3 2 = 3 2 位移单独编码 局部码 由单元的结点 位移总码组成 的向量 128-4
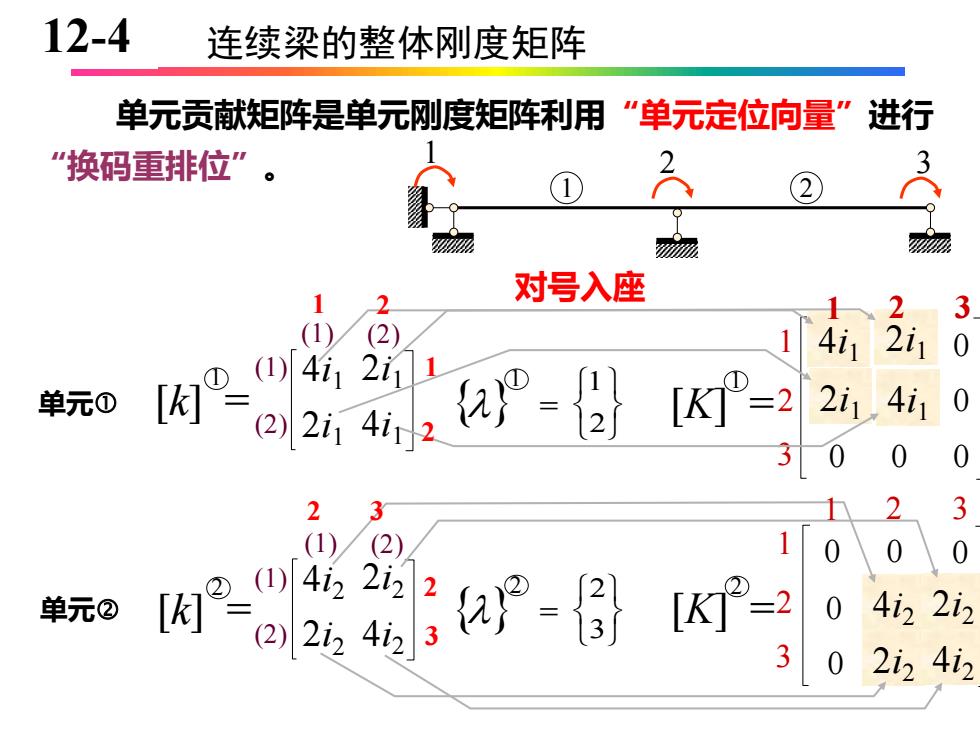
12-4 连续梁的整体刚度矩阵 单元贡献矩阵是单元刚度矩阵利用“单元定位向量”进行 “换码重排位”。 3 ② 2 1 对号入座 (1)(2) 2. 3 4i1 2i1 0 (1)4121 单元① [ 0 (2)1 [”-2 2i1 4i1 3 0 0 0 2 3 2 3 (1)/(2) ②(1) 单元® 3a-6[=2 4i2 0 2i24i2
10-4 连续梁的整体刚度矩阵 单元 单元 [k] = 4i1 2i1 4i1 2i 1 1 (1) (2) (1) (2) 1 = 2 1 [K] =1 1 2 3 0 0 0 0 0 0 0 0 0 4i1 2i1 2i1 4i1 1 2 3 [k] = 4i2 2i2 4i2 2i 2 2 (1) (2) (1) (2) 2 = 3 2 [K] =2 0 0 0 0 0 0 0 0 40i2 2i2 4i2 2i2 1 2 3 1 2 3 单元贡献矩阵是单元刚度矩阵利用“单元定位向量”进行 “换码重排位”。 2 3 2 3 1 2 2 1 对号入座 1 2 1 2 3 128-4