
12-3 整体坐标系下的单元刚度矩阵 ✉> {F}o=[T]{F9 cosa sing 0 0 0 0 -sina cosa 0 0 0 0 0 0 0 0 0 [r]= 0 0 0: cosa sina 0 0 0 0-sina cosa 0 0 0 0 0 坐标转换矩阵(正交矩阵) +[T]4=[T]
10-3 整体坐标系下的单元刚度矩阵 F T F = cos sin 0 0 0 0 sin cos 0 0 0 0 0 0 1 0 0 0 0 0 0 cos sin 0 0 0 0 sin cos 0 0 0 0 0 0 1 T − = − 1 T T T − = 坐标转换矩阵(正交矩阵) e e 128-3
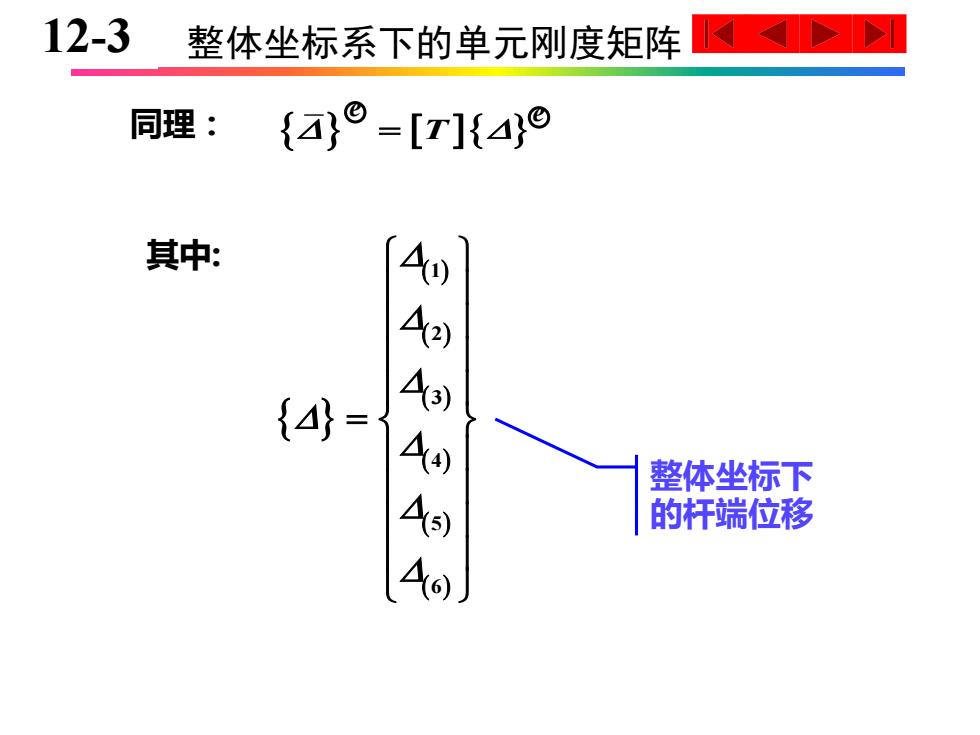
12-3 整体坐标系下的单元刚度矩阵 同理:{a}°-[T]{a© 其中: 4 1 {4 4 整体坐标下 的杆端位移
10-3 整体坐标系下的单元刚度矩阵 同理: = T ( ) ( ) ( ) ( ) ( ) ( ) 1 2 3 4 5 6 = 其中: 整体坐标下 的杆端位移 e e 128-3

12-3 整体坐标系下的单元刚度矩阵 1整体坐标系下的单元刚度矩阵 局部 {回°=[kJ©④ {Fy°=[rj'[]r]{4 {F}©=[r]{F9 {F}©=[k49 由 {4©=[T]{49 整体坐标下的单 [r]{Fy9=[k]©[T]{4 元刚度方程 {ko=[r]'[]r] (8-23) {Fe=[r]'[k][r]{48 整体坐标下的 {r}'=[r]' 元刚度矩阵
10-3 整体坐标系下的单元刚度矩阵 1 整体坐标系下的单元刚度矩阵 F k = e e e T F k T = e e e 1 F T k T − = e e e T F T k T = e e e T k T k T = e e F k = e e e 1 T T T − = 整体坐标下的 元刚度矩阵 局部 F T F T = = e e 由 e e 整体坐标下的单 元刚度方程 8-3 (8 23) − 12-
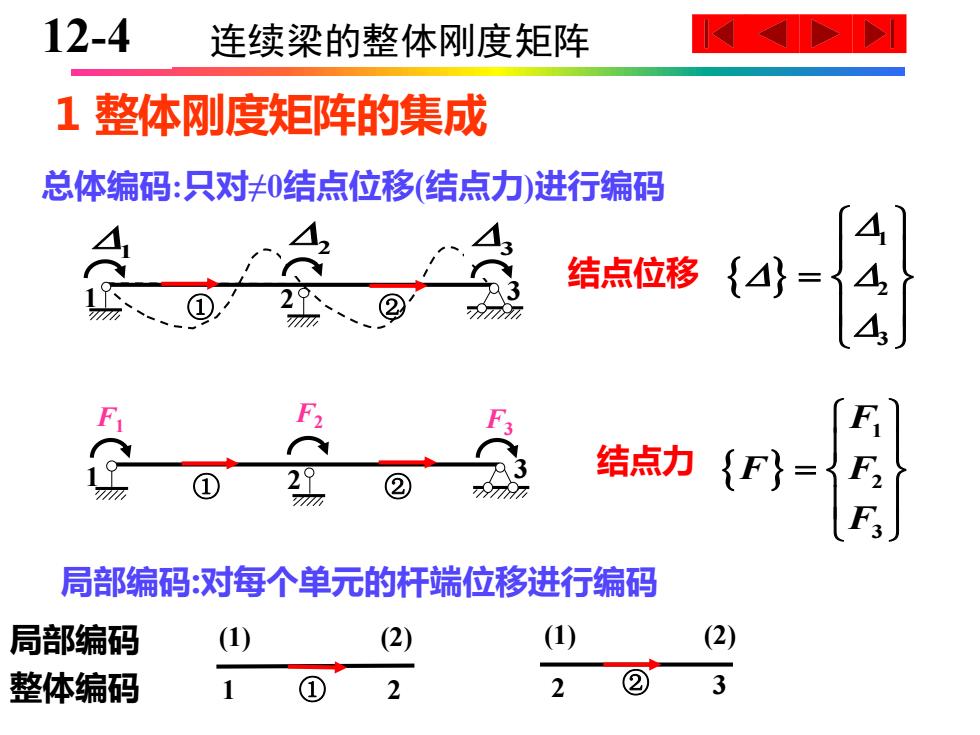
12-4 连续梁的整体刚度矩阵 1整体刚度矩阵的集成 总体编码:只对0结点位移(结点力)进行编码 A 结点位移 {= 、① ② F Q 结点力 ② {F}= F 局部编码:对每个单元的杆端位移进行编码 局部编码 (1) (2) (1) (2) 整体编码 ① 2 2 3
10-4 连续梁的整体刚度矩阵 1 整体刚度矩阵的集成 2 3 总体编码:只对≠0结点位移(结点力)进行编码 1 ① 2 ② 1 3 1 2 3 = ① 2 ② 3 1 F1 F2 F3 1 2 3 F F F F = (1) (2) ① (1) (2) ② 局部编码:对每个单元的杆端位移进行编码 1 2 2 3 结点位移 结点力 局部编码 整体编码 128-4
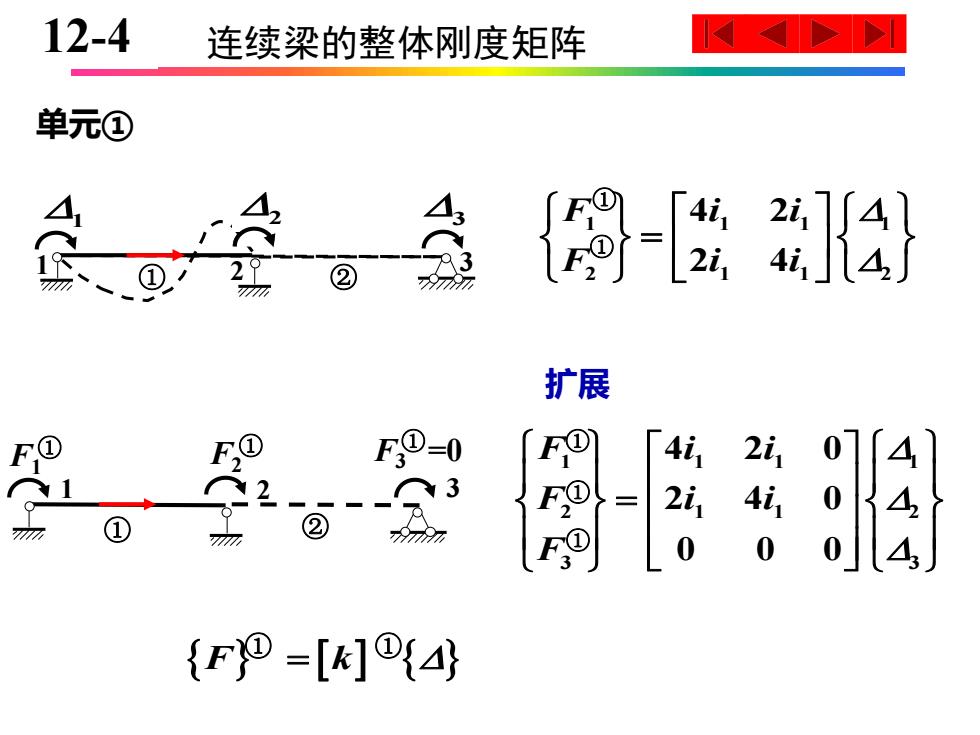
12-4 连续梁的整体刚度矩阵 单元① 、 ① ② 3 扩展 FD-0 2i1 2 3 F9= ① n ② F 0 (F =[k](4
10-4 连续梁的整体刚度矩阵 1 2 3 ① 2 ② 1 3 单元① 1 1 1 1 2 1 1 2 4 2 2 4 F i i F i i = ① ① 1 1 1 1 2 1 1 2 3 3 4 2 0 240 0 0 0 F i i F i i F = ① ① ① 扩展 ① ② 1 2 3 F1 F2 ① ① F3 ①=0 2 F k = ① ① 128-4