
Chap 1.2 极限
Chap 1.2 极 限
1.2.1概念 口x→+0时的函数极限 若自变量x的值无限增大时,函数f(x)无限趋 近于常数A,则称函数f(x)当x→+∞时极限为 A或收敛于A,记作 limf(x)=A或f(x)→A(当x→∞时) >极限是一种变化的定量趋势:与A的接近程度f(x)-A 可以任意小(只要x充分大) A X 0
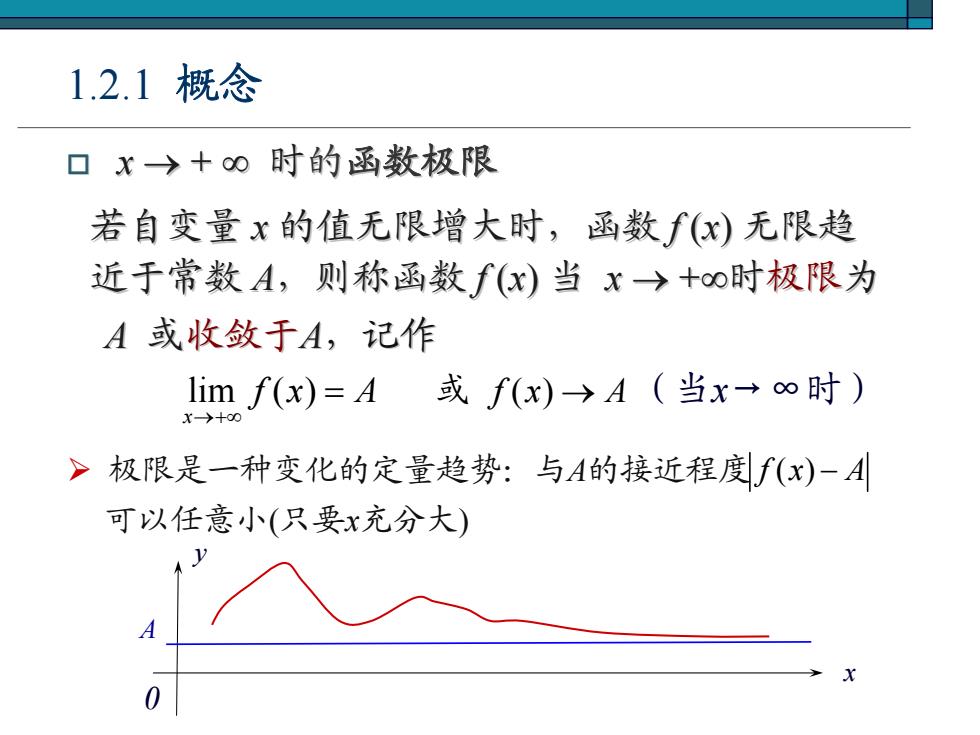
x → + ∞ 时的函数极限 1.2.1 概念 ¾ 极限是一种变化的定量趋势:与A的接近程度 lim ( ) x f x A →+∞ = 或 f ( ) x A → (当x→∞时) f ( ) x A − 可以任意小(只要x充分大) y 0 x A 近于常数 A,则称函数 f (x) 当 x → +∞时极限为 若自变量 x 的值无限增大时,函数 的值无限增大时,函数 f (x) 无限趋 A 或收敛于A,记作

>极限的这样定义是描述性的,真正科学严格 的定义由数学大师柯西与魏尔斯特拉斯完成 柯西Augustin Louis Cauchy (1789-1857) >19世纪最卓越的数学家之一,论文 800余篇(26卷),数量仅次于Euler >给出了微积分一系列基本概念的严格 定义,包括极限定义(经过维尔斯特拉 斯的加工) >1805年进入高等工业学校学习,打算成为土木工程师, 因数学上的成就被推荐为科学院院士
¾ 极限的这样定义是描述性的,真正科学严格 的定义由数学大师 柯西与魏尔斯特拉斯完成 柯西 Augustin Louis Cauchy (1789-1857) ¾ 19世纪最卓越的数学家之一,论文 800余篇(26卷),数量仅次于Euler ¾ 给出了微积分一系列基本概念的严格 定义,包括极限定义(经过维尔斯特拉 斯的加工) ¾ 1805年进入高等工业学校学习,打算成为土木工程师, 因数学上的成就被推荐为科学院院士

现代分析之父魏尔斯特拉斯 Weierstrass,Karl Theodor Wilhelm 1815-1897) >函数论的奠基者,以科学的语言,系统建 立了实分析和复分析的基础 >1834年在波恩大学学法律和财政后转学数学,在中学教 写作与体育,41岁才任柏林大学讲师 >卓越的教师,讲课朴实无华,循循善诱;柏林大学第一 个数学讨论班,学生中约100名正教授,包括著名的俄国女科 学家柯瓦列夫斯卡娅
( Weierstrass, Karl Theodor Wilhelm 1815-1897 ) ¾ 1834年在波恩大学学法律和财政后转学数学,在中学教 写作与体育,41岁才任柏林大学讲师 ¾ 函数论的奠基者,以科学的语言,系统建 立了实分析和复分析的基础 ¾ 卓越的教师,讲课朴实无华,循循善诱;柏林大学第一 个数学讨论班,学生中约100名正教授,包括著名的俄国女科 学家柯瓦列夫斯卡娅 现代分析之父 魏尔斯特拉斯
1 例1)lim二=0, 2)limg=0,(0<g<1) x→+0X X>十00 3)lim arctanx= 4)lim sinx=? X→+00 2 >X→一∞时的函数极限怎样描述? lim f(x)=4 X-→-00 lim 1=? limq④=0,(q?) lim arctanx=? x→-0X X)-00
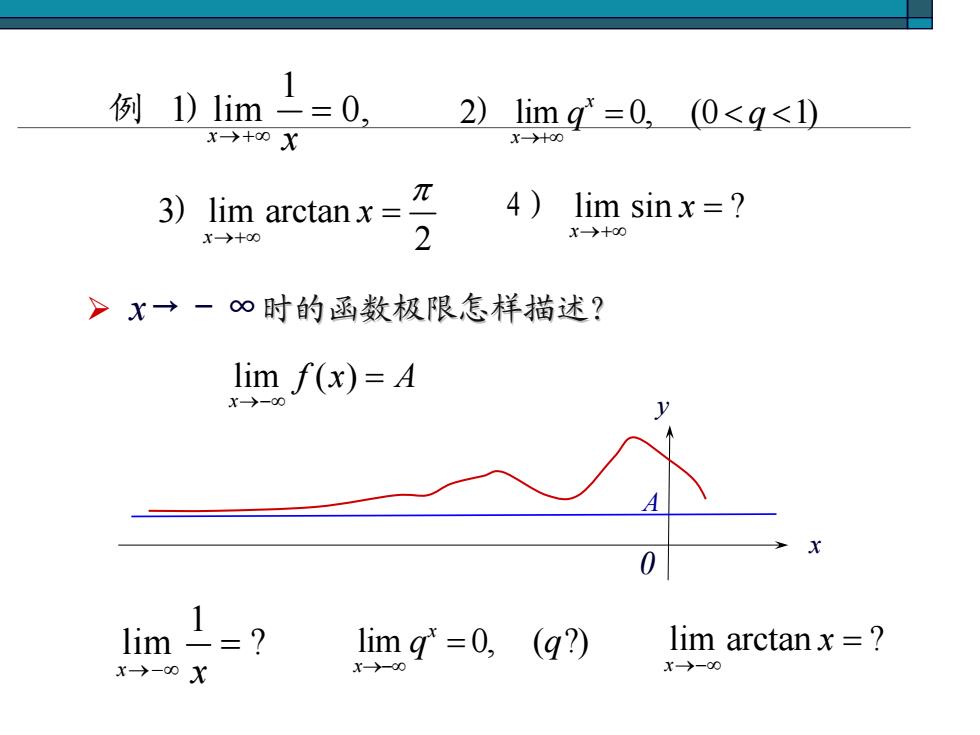
3 lim arctan x 2 x π →+∞ ) = 1 1 lim 0, x→+∞ x 例 ) = 2 lim 0, (0 1) x x q q →+∞ ) = < < ¾ x→-∞时的函数极限怎样描述? 时的函数极限怎样描述? lim ( ) x f x A →−∞ = 0 x A y 1 lim ? x→−∞ x = lim 0, ( ?) x x q q →−∞ = lim arctan ? x x →−∞ = lim sin ? x x →+∞ 4) =