
Chap 2 导数和微分
Chap 2 导数和微分

Chap 2.1 导数的概念
Chap 2.1 导数的概念

2.1.1 例子 速度 运动物体的路程函数S() 时间从t0→t+△t,路程△S=S(t+△t)-S(to) △S 平均速度: △t 时刻的瞬时速度: △S lim=lim S(t+△t)-S(t) △1-→0△t △1-→0 △t 斜率 求函数曲线y=f(x)上点M(xyo)处的切线
2.1.1 例子 速度 运动物体的路程函数 S(t) 时间从t0→t0+Δt,路程ΔS= S(t0+Δt)-S(t0) 平均速度: tSΔΔ t0时刻的瞬时速度: t tSttS t S t t Δ Δ+ − = Δ Δ →Δ →Δ )()( lim lim 0 0 0 0 ■ 斜率 求函数曲线y = f (x)上点M0(x0,y0)处的切线
设MM是过M点的割线,沿曲线M→M, N o+Ay M 割线极限位置的直线 即切线 割线斜率: Yo M △y_f(x+△x)-f(x) xo+Ax △x △x 切线斜率: lim Ay lim f(x+△x)-f(x) △r→0△x x→0 △x
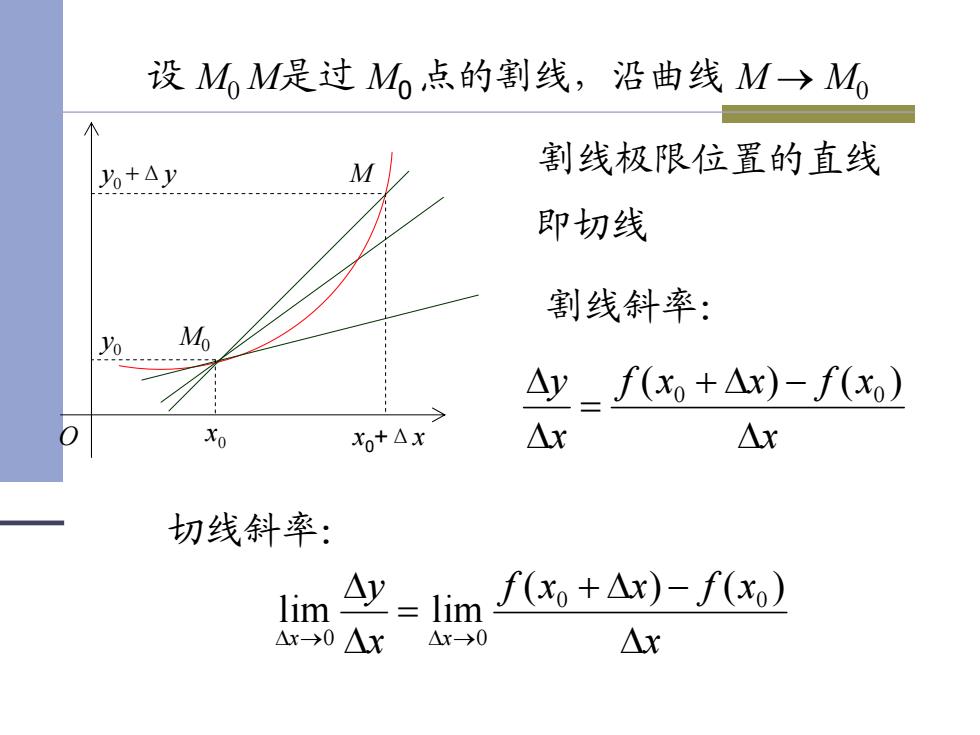
x0 y0 x0+Δx y0 +Δy M0 M O 设 M0 M是过 M0 点的割线,沿曲线 M → M0 割线极限位置的直线 即切线 割线斜率: x xfxxf x y Δ + Δ − = Δ Δ )()( 0 0 切线斜率: x xfxxf x y x x Δ + Δ − = Δ Δ →Δ →Δ )()( lim lim 0 0 0 0

细菌增殖速度 设一菌群在某一时刻t的细菌数为N() 求该菌群在时刻t。的增殖速度v(o) t,>t+△t一段的平均增殖速度 △N_N(t。+△t)-m(to) △t △t t,,点的增殖速度 AN v(to)=lim=lim N(t。+△t)-N() △-→0△t △x→0 △t
细菌增殖速度 设一菌群在某一时刻 设一菌群在某一时刻t 的细菌数为 N (t) 求该菌群在时刻 求该菌群在时刻t0 的增殖速度 v(t0) t0 → t0+Δt 一段的平均增殖速度 0 0 N Nt t mt ( ) () t t Δ + Δ − = Δ Δ t0 点的增殖速度 0 0 0 0 0 ( ) () ( ) lim lim t x N Nt t Nt v t t t Δ→ Δ→ Δ +Δ − = = Δ Δ