
Chap 2.4 微分中值定理和 导数的应用
Chap 2.4 微分中值定理和 导数的应用
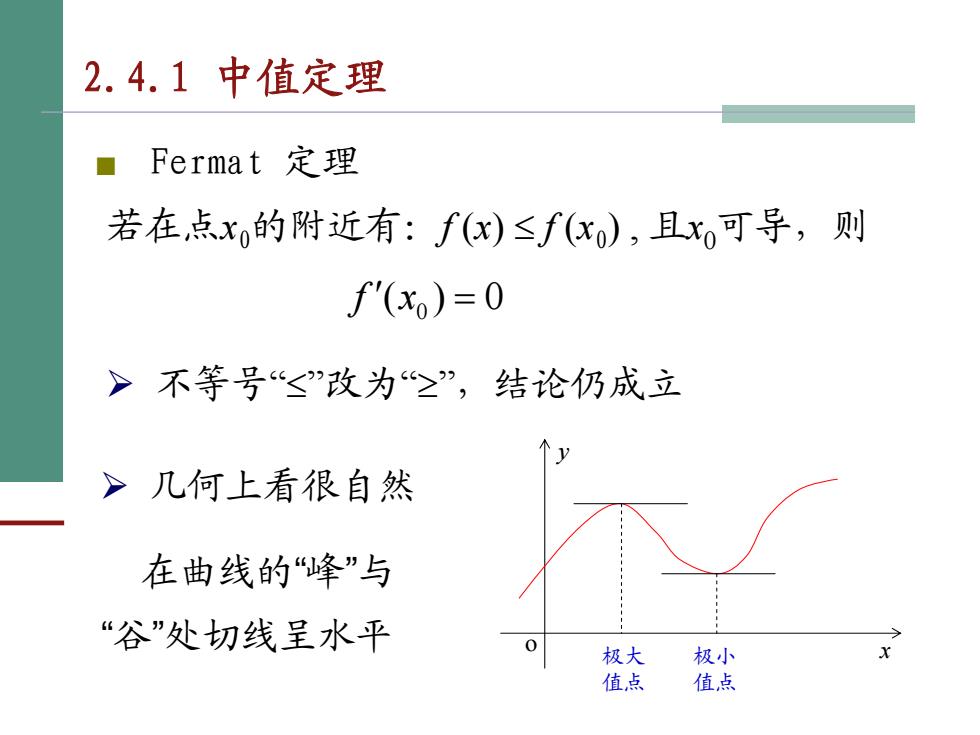
2.4.1中值定理 ■ Fermat定理 若在,点x的附近有:f(x)≤f(x),且x可导,则 f'(x0)=0 >不等号“≤”改为≥”,结论仍成立 >几何上看很自然 在曲线的“峰”与 “谷”处切线呈水平 极大 极小 值点 值点
若在点x0的附近有:f (x) ≤ f (x0) , 且x0可导,则 2.4.1 中值定理 ■ Fermat 定理 0)(′ xf 0 = ¾ 几何上看很自然 在曲线的“峰”与 o x y 极大 值点 极小 值点 “谷”处切线呈水平 ¾ 不等号“≤”改为“≥”,结论仍成立
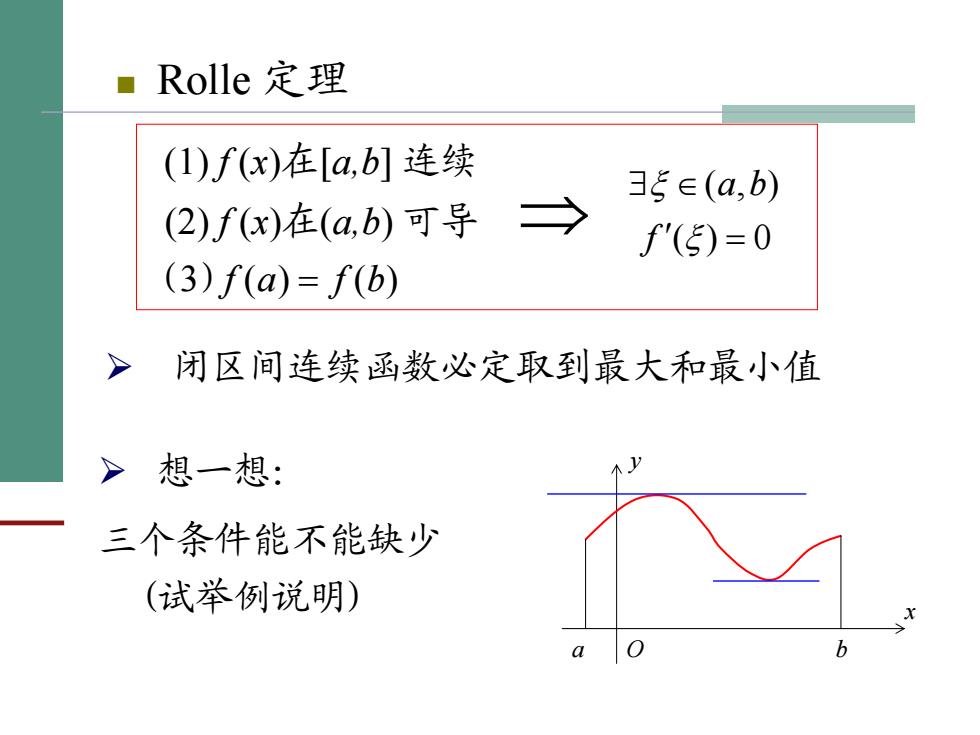
■Rolle定理 (1)f(x)在[a,b]连续 35∈(a,b) (2)f(x)在(a,b)可导 → f'(5)=0 (3)f(a)=f(b) 闭区间连续函数必定取到最大和最小值 >想一想: 三个条件能不能缺少 (试举例说明) 6
■ Rolle 定理 )( = bfaf )()(3 ⇒ 0)( ),( ′ = ∃ ∈ξ ξf ba (1) f (x)在[a,b] 连续 (2) f (x)在(a,b) 可导 ¾ 闭区间连续函数必定取到最大和最小值 a b O x y ¾ 想一想: 三个条件能不能缺少 (试举例说明)
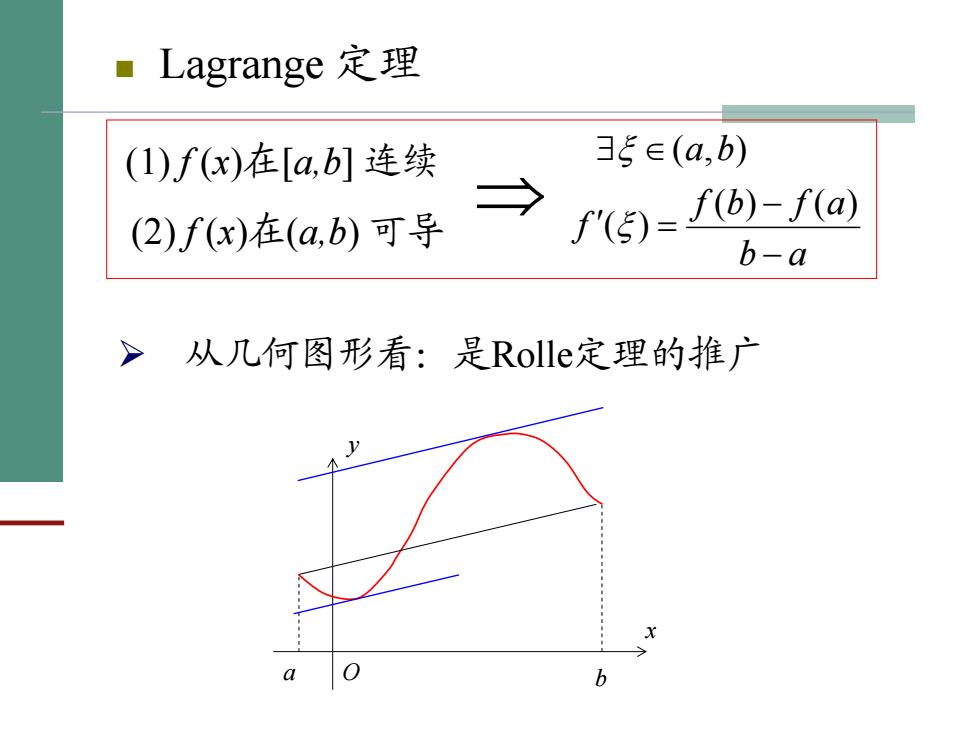
Lagrange定理 (1)f(x)在[a,b]连续 35∈(a,b) (2)f(x)在(a,b)可导 f"5)=f)-fa) b-a >从几何图形看:是Rolle2定理的推广
■ Lagrange 定理 ⇒ ab afbf f ba − − ′ = ∃ ∈ )()( )( ),( ξ ξ ¾ 从几何图形看:是Rolle定理的推广 a O b x y (1) f (x)在[a,b] 连续 (2) f (x)在(a,b) 可导

>证明的方法 辅助函数法:改变结论形式来分析 推论1 f'(x)=0(x∈I)→f(x)=c(x∈I) ■ 推论2 f'(x)=g'(x)(x∈I) →f(x)-8(x)=c(x∈I)
■ 推论 2 ⇒ = ∈ Ixcxf )()( ¾ 证明的方法 辅助函数法:改变结论形式来分析 ■ 推论 1 ′ = ∈ Ixxf )(0)( f x gx x I ′ ′ () () ( ) = ∈ ⇒ f () () ( ) x − g x cxI = ∈