
导航 微训练设平面a的法向量为1,2,-2),平面的法向量为(-2,4,), 若alB,则k的值为() A.2B.-4 C.4 D.-2 答案:C
导航 微训练 设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k), 若α∥β,则k的值为( ) A.2 B.-4 C.4 D.-2 答案:C

导航 课堂·重难突破 求平面的法向量 典例剖析 1.已知平面a经过三点A(1,2,3),B(2,0,-1),C3,-2,0),求平面a的 一个法向量
导航 课堂·重难突破 一 求平面的法向量 典例剖析 1.已知平面α经过三点A(1,2,3),B(2,0,-1),C(3,-2,0),求平面α的 一个法向量

导航 解:由题意可知,AB=(1,-2,-4),AC=(2,-4,-3) 设平面a的法向量为n=(cy,z), 则t=0化2w2 nAc=0,印1 所以比=2y, z=0. 令y=1,则x=2. 所以平面a的一个法向量为n=(2,1,0)
导航 解:由题意可知,𝑨 𝑩 =(1,-2,-4),𝑨 𝑪 =(2,-4,-3). 设平面 α 的法向量为 n=(x,y,z), 则 𝒏·𝑨 𝑩 = 𝟎, 𝒏·𝑨 𝑪 = 𝟎, 即 𝒙-𝟐𝒚-𝟒𝒛 = 𝟎, 𝟐𝒙-𝟒𝒚-𝟑𝒛 = 𝟎, 所以 𝒙 = 𝟐𝒚, 𝒛 = 𝟎. 令y=1,则x=2. 所以平面α的一个法向量为n=(2,1,0)
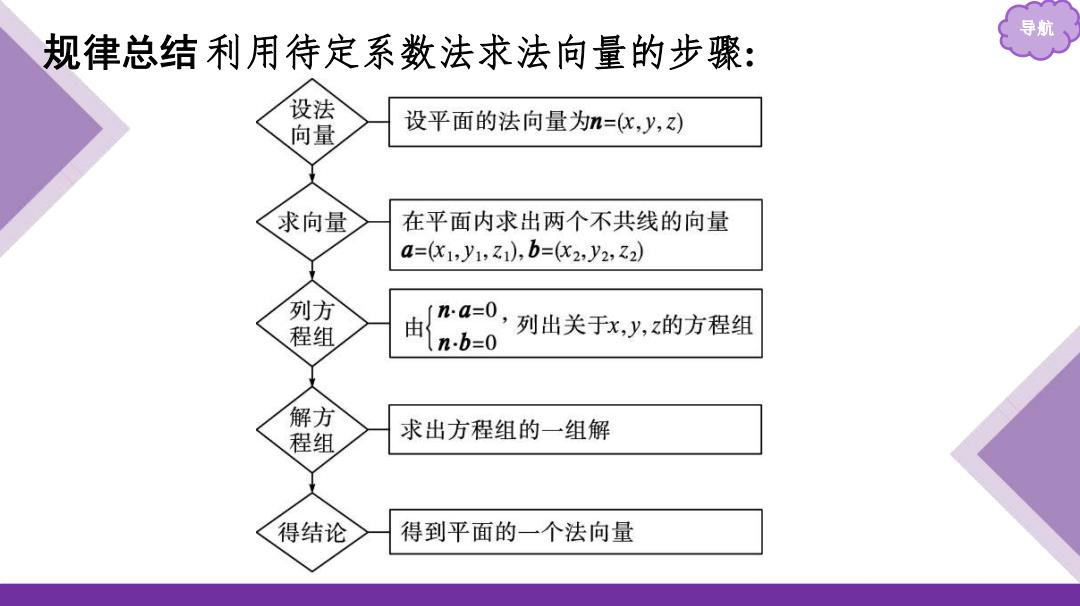
导航 规律总结利用待定系数法求法向量的步骤: 设法 向量 设平面的法向量为n=(x,y,z) 求向量 在平面内求出两个不共线的向量 a=(x1,y1,z1),b=(c2,y2,2) 列方 n.a=0, 程组 由 n-b=0 列出关于x,y,z的方程组 解方 程组 求出方程组的一组解 得结论 得到平面的一个法向量
导航 规律总结 利用待定系数法求法向量的步骤: