
例6 求由心形线p=a(1+cos)所围成的图形的面积.(a>0)解 dA=_a'(1+ cos0)~dede2利用对称性知A = 2._a f" (1 + cos 0)°d2= a2 [" (1 + 2 cos 0 + cos? 0)d07元33-22Asin 20+2sin+=元aa1324Jo
解 dA a d 2 2 (1 cos ) 2 1 利用对称性知 . 2 3 2 a d d 2 (1 cos ) 0 2 2 1 A 2 a (1 2cos cos )d 2 0 2 a sin 2 4 1 2sin 2 2 3 a 0 6 (1 cos ) .( 0) a a 例 求由心形线 所围成的 图形的面积
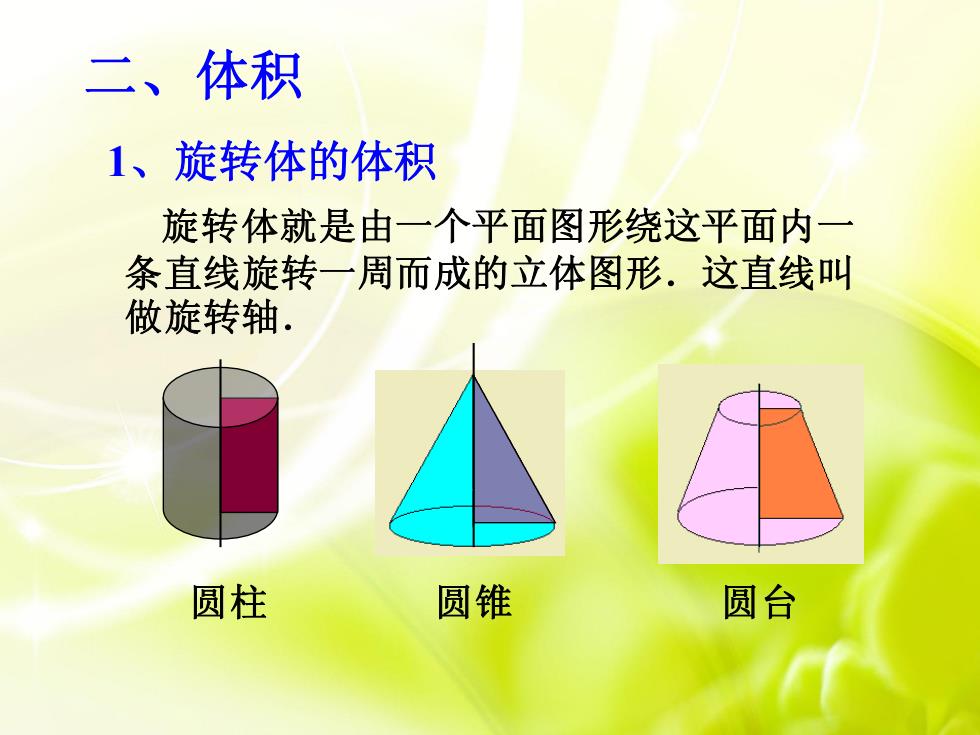
二、 体积1、旋转体的体积旋转体就是由一个平面图形绕这平面内一条直线旋转一周而成的立体图形.这直线叫做旋转轴,圆柱圆锥圆台
旋转体就是由一个平面图形绕这平面内一 条直线旋转一周而成的立体图形.这直线叫 做旋转轴. 圆柱 圆锥 圆台 1、旋转体的体积 二、体积

一般的,如果旋转体是由连续曲线y=f(x)直线x=a、x=b及x轴所围成的曲边梯形绕x轴旋转一周而成的立体,体积为多少?yty=f(x)取x为积分变量xE[a,b]0在[a,b]上任取一小xXx+dxba区间[x,x+dx]取以为底的窄曲边梯形绕x轴旋转而成的薄片的体积为体积元素,dV=元lf(x)dx旋转体的体积为π[f(x)} dx=
取x x a b 为积分变量 [ , ] 2 [ ( )] dx x dV f x dx 取以 为底的窄曲边梯形绕 轴旋转而成的 薄片的体积为体积元素, x x dx x y o 旋转体的体积为 V f x dx b a 2 [ ( )] y f (x) ( ) y f x x a x b x x 一般的,如果旋转体是由连续曲线 、 直线 、 及 轴所围成的曲边梯形绕 轴 旋转一周而成的立体,体积为多少? [ , ] [ , ] a b x x dx 在 上任取一小 区间