
注(1)定积分的本质是个数值;(2) S=f(5,)△x,是与[a,b)的分法及在xi-1,x,li=l上,取法有关;n之F(5,)Ax,是与[a,b)的分法及在xi-1,x,1I = lim2-→0i=1上,取法无关;(3) "f(x)dx =f"f( )d =f"f(udu定积分数值只依赖于被积函数的结构和上、下1111限,而与积分变量的记号无关
11 11 b a f (x)dx = b a f ( )d ( ) [ , ] [ , ] 1 1 i i i n i S f i x a b x − x = = 是 与 的分法及在 lim ( ) [ , ] [ , ] 1 1 0 i i i n i I f i x a b x − x = → = 是 与 的分法及在 (3) 定积分数值只依赖于被积函数的结构和上、下 限, 而与积分变量的记号无关. 上 i取法 有关; 注 上 i取法 无关; = b a f ( )d (1)定积分的本质是个数值; (2)
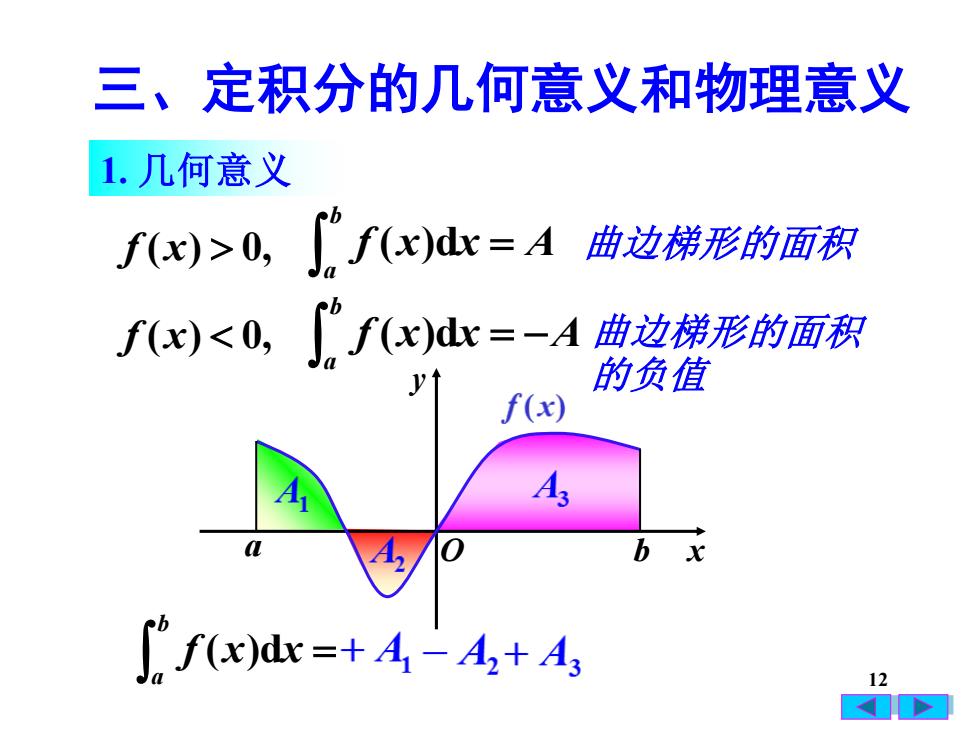
三、定积分的几何意义和物理意义1.几何意义ebL f(x)dx = A曲边梯形的面积f(x) >0,cbf(x)dx=一A曲边梯形的面积f(x)<0,的负值ytf(x)Aa0bxf(x)dx =+ A - A,+ A,12A7
12 f (x) 0, = b a f (x)dx A 曲边梯形的面积 f (x) 0, = − b a f (x)dx A 曲边梯形的面积 的负值 = b a f (x)dx 1. 几何意义 三、定积分的几何意义和物理意义 O x y a b
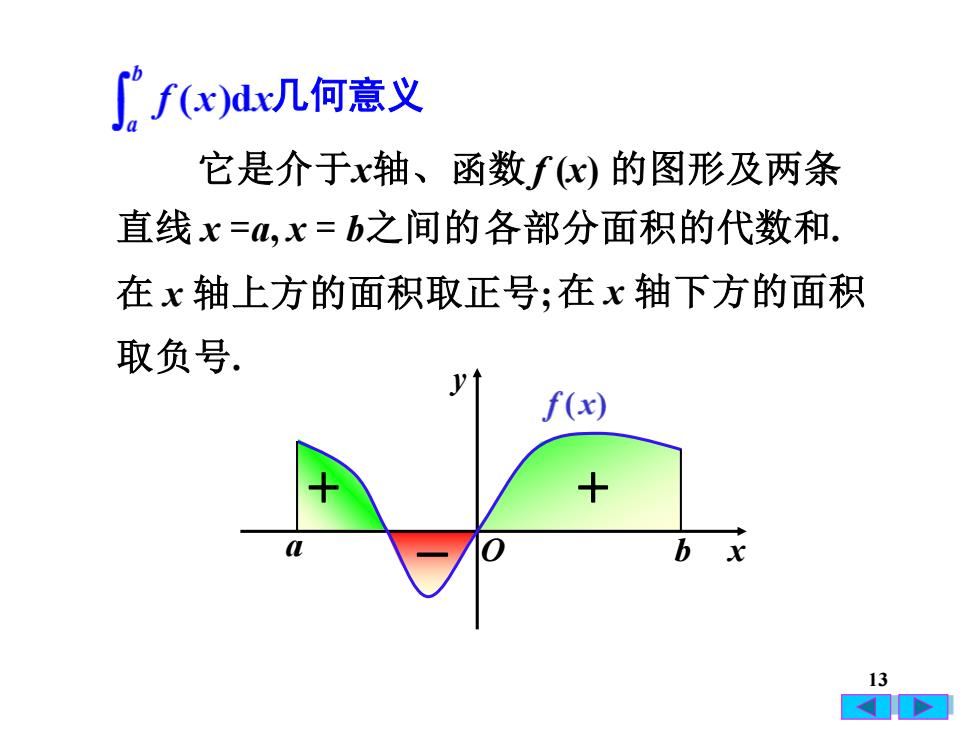
f(x)dx几何意义它是介于x轴、函数f(x)的图形及两条直线x=a.x=b之间的各部分面积的代数和在x轴上方的面积取正号:在x轴下方的面积取负号。Vf(x)++abx13A
13 几何意义 各部分面积的代数和. 取负号. 它是介于x轴、函数 f (x) 的图形及两条 直线 x =a, x = b之间的 在 x 轴上方的面积取正号;在 x 轴下方的面积 O x y a b + − +
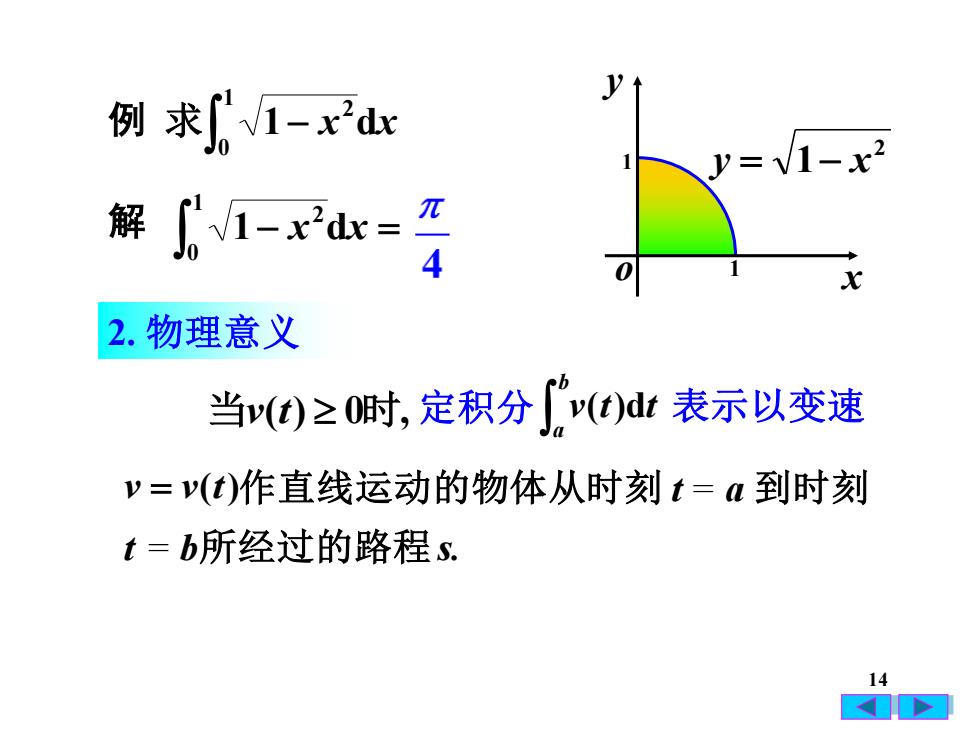
V例求V1-xdx元解"dx :x4ox2.物理意义7v(t)dt 表示以变速当v(t)≥ 0时,定积分1=v(t)作直线运动的物体从时刻t= a到时刻t =b所经过的路程s.14A
14 例 1 x dx 1 0 2 求 − 解 2 y = 1− x 2. 物理意义 当v(t) 0时, t = b所经过的路程 s. v = v(t) o x y 1 1 − = 1 x dx 1 0 2 b a v(t)dt 作直线运动的物体从时刻 t = a 到时刻 定积分 表示以变速