
(4)求极限(量变到质变)为了得到A的精确值,分割无限鼬,即小区间的最大长度=max{△xi,△x2△x,}趋近于零(α一→0)时,取极限,极限就是曲边梯形的面积:nE f(5.)Ax,A = lim→0i16
6 (4) 求极限 面积: ( )时,取极限,极限值就是曲边梯形的 的最大长度 趋近于零 为了得到 的精确值,分割无限加细,即小区间 0 max{ , , } 1 2 → = x x xn A (量变到质变)

思想以不变代变2.求变速直线运动的路程设某物体作直线运动,已知速度V=v(t)是时间间隔[T,Tl上t的一个连续函数,且v(t)≥0求物体在这段时间内所经过的路程思路把整段时间分割成若干小段,每小段上速度看作不变,求出各小段的路程再相加,便得到路程的近似值,最后通过对时间的无限细分过程求得路程的精确值
7 2.求变速直线运动的路程 思想 以不变代变 设某物体作直线运动,已知速度 v = v(t) 是时间间隔 [T ,T ]上t 1 2 的一个连续函数, 且v(t) 0, 求物体在这段时间内所经过的路程. 思路 把整段时间分割成若干小段, 每小段上 速度看作不变,求出各小段的路程再相加, 便 得到路程的近似值, 最后通过对时间的无限 细分过程求得路程的精确值.

(1) 分割 T =t,<ti<t,<...<tn-1<tn=T,At; = t; - ti-14s,表示在时间区间[t;-1,t,]内走过的路程As, ~(2) 取近似(,t; (i =1,2,...n)某时刻的速度nEv(t,)At;(3)求和s~i=1(4)取极限a =max[Ati,△t2,",Atn} 令a → 0Ev(t,)At;s=lim路程的精确值-0i-18
8 (1) 分割 1 0 1 2 1 T2 T t t t t t = n− n = i = i − i−1 t t t i i i s v( )t i i n i s v t = ( ) 1 (4) 取极限 max{ , , , } 1 2 n = t t t 路程的精确值 (2) 取近似 i s (i = 1,2, n) 令 → 0 表示在时间区间 [ , ] 内走过的路程. i 1 i t t − 某时刻的速度 (3)求和

上两例共同点:ZA;1)量具有可加性,I=二、定积分的定2)方法一样;3)结果形式一样定义设函数f(x)在[a,b]正若干个分点a=X<<x<.….<x-1<,=b把区间[a,b分成n个小区间,各小区间长度依次为2△x; = x; -X;-1,(i=1,2,,n),在各小区间上任取一点 5,(5, E △x;), 作乘积f(5,)Ax, (i = 1,2,,n)(3)异作和 S-f(5)Ar,i-1记 =max[△xj,△x2,",△x,},如果不论对[a,b]9A7
9 二、定积分的定义 定义 设函数f (x)在[a,b]上有界,在[a,b]中任意插入 若干个分点 把区间[a,b]分成n个小区间,各小区间长度依次为 ,( 1,2, , ), xi = xi − xi−1 i = n 在各小区间上任取 一点 ( ), i i xi 作乘积 并作和 记 max{ , , , }, = x1 x2 xn 如果不论对 (1) (2) (3) 上两例共同点: I = I; 2) 方法一样; 1) 量具有可加性, 3) 结果形式一样. [a,b]
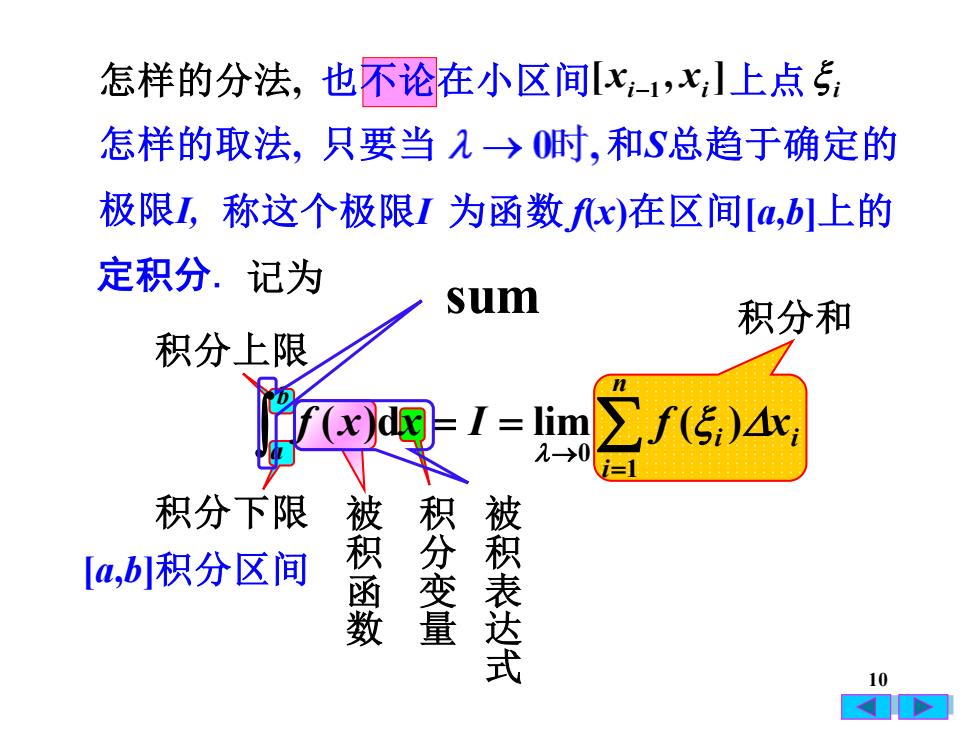
怎样的分法,也不论在小区间[xi-1,x,]上点5怎样的取法,,只要当 α→0时,和S总趋于确定的极限I,称这个极限I 为函数f(x)在区间[a,bl上的定积分.记为sum积分和积分上限Zf(5.)4x,f(x)d- 1 =lim2-→0i-1积分下限积分变量被积表达式被积函数[a,b]积分区间10A
10 被 积 函 数 被 积 表 达 式 记为 积分和 怎样的分法, 也不论在小区间 [ , ] xi−1 xi 上点 i 怎样的取法, 只要当 和S总趋于确定的 极限I, 称这个极限I 为函数 f(x)在区间[a,b]上的 定积分. i n i i b a f x x I f x ( )d lim ( ) 1 0= → = = 积分下限 积分上限 积 分 变 量 [a,b]积分区间 sum