《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用 3-03 第三节 泰勒（Taylor）公式

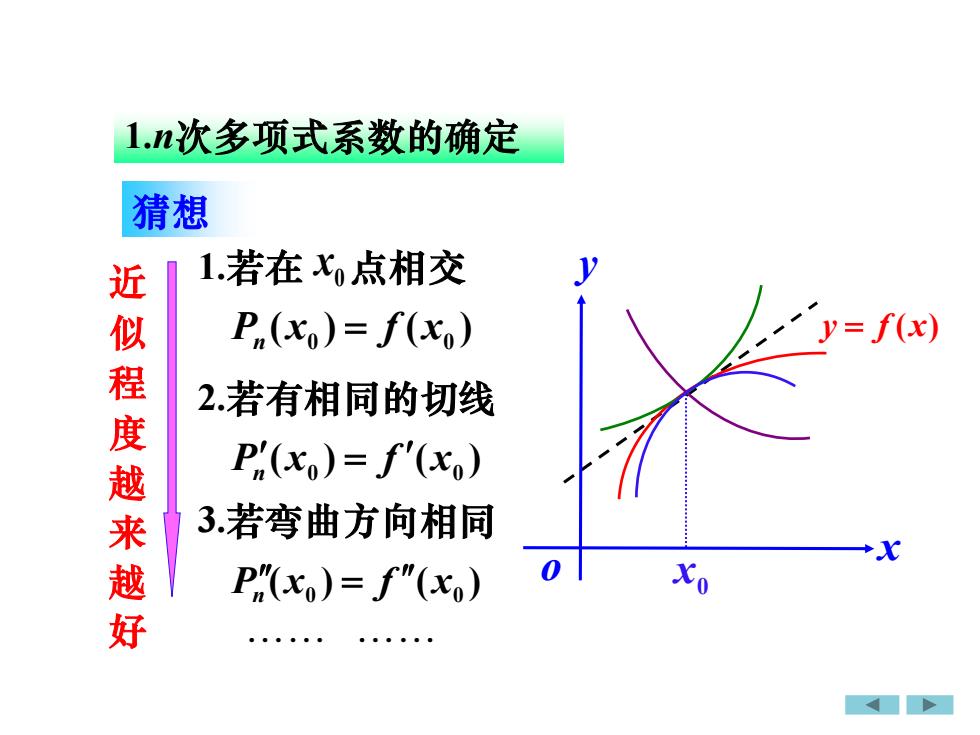
1.n次多项式系数的确定猜想1.若在Xo点相交N近似程度越来越好y= f(x)P,(x) = f(x)2.若有相同的切线P'(x) = f'(xo)3.若弯曲方向相同X0xoP'(xo)= f"(xo)

0 x y = f (x) o x y 猜想 ( ) ( ) 0 0 P x f x n = ( ) ( ) 0 x0 P x f n  =  ( ) ( ) 0 x0 P x f n  =  LL LL 2.若有相同的切线 3.若弯曲方向相同 近 似 程 度 越 来 越 好 1.若在 x0 点相交 1.n次多项式系数的确定

P(*)(xo)= f(k)(xo)k = 0,1,2,..",n假设P()=@+@(x-x)+@(x-x) ++@,(xx)": P,(xo)= ao,又P,(x)= f(xo), :. ao = f(xo),: P'(xo)=ai, 又P(x)= f'(xo), :. 1.a, = f'(xo),同理 2!a, = f"(xo) ... .., n!an = f(n)(xo)得 as=云 ()(x) (k= 0,1,2,,n) 代入 P,(x)中得"(xo)P(x)=f(xo) +f'(x)(x -x)+ :(x-x)2!+F("(x)(x-xo)"n!

( ) , Pn x0 = a0 1 ( ), 1 x0   a = f  2! ( ) 2 x0 a = f  L L , ( ) ! 1 0 ( ) f x k a k 得 k = ( ) ( ) 0 ( ) 0 ( ) P x f x k k n = ! ( ) 0 ( ) n a f x n  n = 假设 ( ), 0 x0 ( ) ( ),a = f 0 x0 P x f 又 n = ( ) , Pn x0 = a1   ( ) ( ), 0 x0 P x f n 又  =  同理 0 0 0 0 k = 0,1,2, L ,n 代入 P ( x) n 中得 Pn (x) = n (x x ) L + − 0 (k = 0,1,2, L ,n) 2 0 f (x0 ) ( ) + (x − x ) 0 + ( ) x − x 0 f  x 2! ( ) x0 f  ! ( ) 0 ( ) n f x n n n n a x x P x a a x x a x x ( ) ( ) ( ) ( ) 0 2 0 1 0 2 0 + − = + − + − + L

f"(x(x-x) +P,(x) = f(x)+ f'(x,)(x-x,)+2!(x-x)"n!称为f(x)的泰勒多项式下面将证明确实可以用泰勒多项式来逼近函数f(x),并估计它的误差P,(x) ~ f(x), R,(x)= f(x)-P(x)

n n n x x n f x x x f x P x f x f x x x ( ) ! ( ) ( ) 2! ( ) ( ) ( ) ( )( ) 0 0 ( ) 2 0 0 0 0 0 + − − +  = +  − + L 称为f(x)的 P (x) f (x), n  R (x) f (x) P (x). n = − n 泰勒多项式来逼近 f ( x), 并估计它的误差. 下面将证明确实可以用 函数 泰勒多项式

2.泰勤(Taylor)中值定理泰勒(Taylor)中值定理若f(x)在(xE)(a,b)内有 (n+1)阶导数,则当xE(a,b)时,f(x)可表为(x- x)的一个n次多项式与一个余项R,(x)之和：(residual)f"(xo)f(x) =f(x)+ f(x)(x-x)+(x-x)2!x-x)"+ R,(x)n!(n+)2n+1其中 R,(x)(在x,与x之间)x(n + 1)!

泰勒(Taylor)中值定理 f (x) = n n x x n f x x x f x f x f x x x ( ) ! ( ) ( ) 2! ( ) ( ) ( )( ) 0 0 ( ) 2 0 0 0 0 0 + + − −  +  − + L R (x) + n 1 0 ( 1) ( ) ( 1)! ( ) ( ) + + − + = n n n x x n f R x  其中 ( ). 在x0 与x之间 余项 2.泰勒(Taylor)中值定理 多项式 (residual) ( ) ( )( , ) ( 1) , 若 f x 在 x0  a b 内有 n + 阶导数 则当x(a,b)时, f ( x)可表为( x - x0 )的一个n次 与一个余项 R ( x)之和 : n

(x)= (x0)+ I(x)(x- x0)+ I"(m)(x-x,)2!- xo)" + R,(x)n!(n+1)()其中R,(x)x)"+1 (在x,与x之间)x-(n + 1)!分析即证R,(x)= f(x)-P(x)(n+1)(5)(在x,与x之间)(x -x)"+1R,(x)(n + 1)!也即证f(n+1)()R,(x)f()4( (x)(x-x,)n+1(n + ) n+1(n + 1)!

分析 R (x) f (x) P (x). 即证 n = − n 1 0 ( 1) ( ) ( 1)! ( ) ( ) + + − + = n n n x x n f R x  ( ). 在x0 与x之间 = − +1 0 ( ) ( ) n n x x R x ( 1)! ( ) ( 1) + + n f n  也即证 ( 1)! ( ) ( 1) + = + n f n  1 0 ( ) ( ) ( ) + − − n n x x f x P x 2 0 0 0 0 0 ( ) 2! ( ) ( ) ( ) ( )( ) x x f x f x f x f x x x −  = +  − + 1 0 ( 1) ( ) ( 1)! ( ) ( ) + + − + = n n n x x n f R x  其中 ( ). 在x0 与x之间 ( ) ( ) ! ( ) 0 0 ( ) x x R x n f x n n n +L+ − +