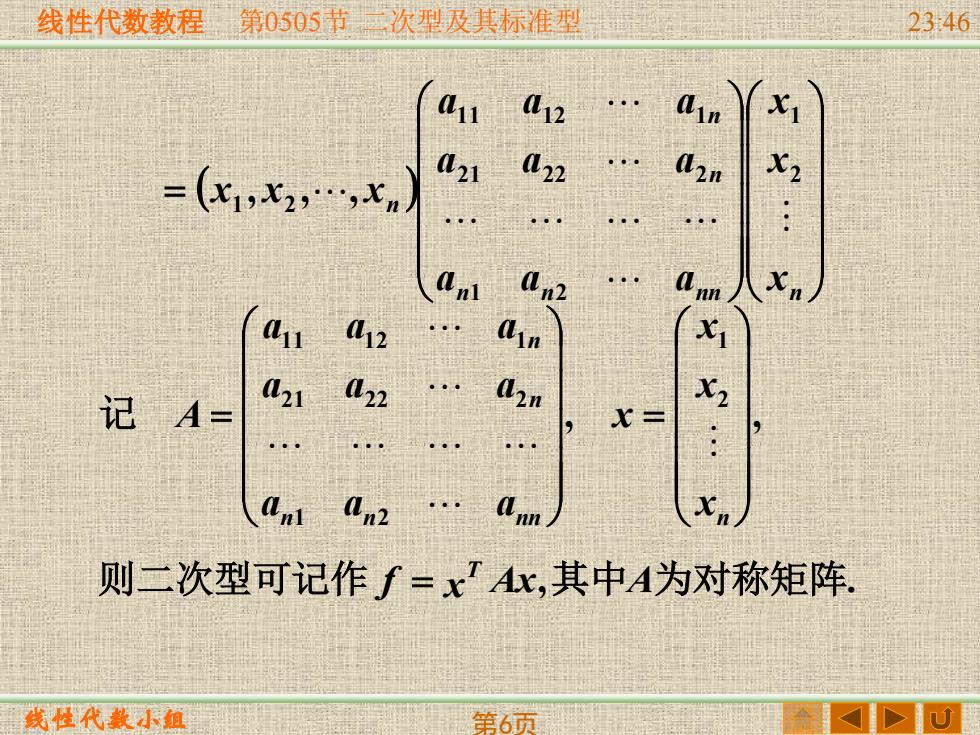
线性代数教程第0505节三次型及其标准型 2346 11 L12 Cin U21 l22 Q2n x2 =(比1,x2,xn l 2 41 012 n L21 l22 . 记 A A2n x= n 0n2 则二次型可记作f=x?Ax,其中A为对称矩阵 线性代数小组 第6页
线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第6页 则二次型可记作 f x Ax,其中A为对称矩阵. T = , , 2 1 1 2 2 1 2 2 2 1 1 1 2 1 = = n n nn n n n x x x x a a a a a a a a a A 记 ( ) = n n nn n n n n x x x a a a a a a a a a x x x 2 1 1 2 2 1 2 2 2 1 1 1 2 1 1 2 , ,

线性代数教程 第0505节三次型及其标准型 23:46 三、二次型的矩阵及秩 在二次型的矩阵表示中,任给一个二次型, 就唯一地确定一个对称矩阵;反之,任给一个对 称矩阵,也可唯一地确定一个二次型.这样,二 次型与对称矩阵之间存在一一对应的关系. 对称矩阵A叫做二次型f的矩阵; f叫做对称矩阵A的二次型; 对称矩阵4的秩叫做二次型f的秩 线性代数小组 第页
线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第7页 三、二次型的矩阵及秩 在二次型的矩阵表示中,任给一个二次型, 就唯一地确定一个对称矩阵;反之,任给一个对 称矩阵,也可唯一地确定一个二次型.这样,二 次型与对称矩阵之间存在一一对应的关系. 对称矩阵A叫做二次型 f 的矩阵; f 叫做对称矩阵A的二次型; 对称矩阵A的秩叫做二次型 f 的 秩

线性代数教程第0505节三次型及其标准型 2346 例1写出二次型 f=x2+2x2-3x3+4xx2-6x2x3 的矩阵 解01=1,02=2,03=-3, 02=021=2,03=031=0, 023=032=-3. 2 .A= 2 2 0 -3-3 线性代数小组 第8项
线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第8页 解 a 1, a 2, a 3, 11 = 22 = 33 = − a a 2, 12 = 21 = a a 0, 13 = 31 = a a 3. 23 = 32 = − . 0 3 3 2 2 3 1 2 0 − − A = − . 2 3 4 6 1 2 2 3 2 3 2 2 2 1 的矩阵 写出二次型 f = x + x − x + x x − x x 例1

线性代数教程第0505节三次型吸其标准型 23:46 四、化二次型为标准形 对于二次型,我们讨论的主要问题是:寻求 可逆的线性变换,将二次型化为标准形. 设 x1=cuy1+C12y2++cinyn2 X2=C21y1+C22y2++c2nyn? xn =cnly+en2y2++Cmyn 记C=(c),则上述可逆线性变换可记作 x=Cy 线性代数小组 第9页
线性代数教程 线性代数小组 第0505节 二次型及其标准型 23:46 第9页 = + + + = + + + = + + + n n n nn n n n n n x c y c y c y x c y c y c y x c y c y c y 1 1 2 2 2 2 1 1 2 2 2 2 1 1 1 1 1 2 2 1 , , 设 四、化二次型为标准形 对于二次型,我们讨论的主要问题是:寻求 可逆的线性变换,将二次型化为标准形. C (c ), 记 = ij 则上述可逆线性变换可 记作 x = Cy