
导航 (2)如何区分一个问题是“分类”还是“分步”? 提示:若完成这件事,可以分几种情况,每种情况中任何一种 方法都能完成任务,则是分类;若从其中一种情况中任取一种 方法只能完成任务的一部分,且只有依次完成各种情况,才能 完成这件事,则是分步
导航 (2)如何区分一个问题是“分类”还是“分步”? 提示:若完成这件事,可以分几种情况,每种情况中任何一种 方法都能完成任务,则是分类;若从其中一种情况中任取一种 方法只能完成任务的一部分,且只有依次完成各种情况,才能 完成这件事,则是分步

导 微训练2已知x∈{2,3,7y∈{-3,4,8),则y可表示不同的值的 个数为( 】 A.10 B.6 C.8 D.9 答案:D 解析:因为x从集合{2,3,7}中任取一个值,共有3个不同的值, 从集合{-3,-4,8}中任取一个值,共有3个不同的值,所以y可表 示3X3=9个不同的值
导航 微训练2已知x∈{2,3,7},y∈{-3,-4,8},则xy可表示不同的值的 个数为( ) A.10 B.6 C.8 D.9 答案:D 解析:因为x从集合{2,3,7}中任取一个值,共有3个不同的值,y 从集合{-3,-4,8}中任取一个值,共有3个不同的值,所以xy可表 示3×3=9个不同的值

导航 课堂·重难突破 一分类加法计数原理 典例剖析 1.所有的两位数中,个位数字大于十位数字的两位数共有多 少个?
导航 一 分类加法计数原理 典例剖析 1.所有的两位数中,个位数字大于十位数字的两位数共有多 少个? 课堂·重难突破

解:方法一:按十位上的数字分别是1,2,3,4,5,6,7,8分成8类,在 每一类中满足条件的两位数分别有8个、7个、6个、5个、4 个、3个、2个、1个 根据分类加法计数原理,满足条件的两位数的个数共有 8+7+6+5+4+3+2+1=36. 方法二:按个位上的数字分别是2,3,4,5,6,7,8,9分成8类,在每 一类中满足条件的两位数分别有1个、2个、3个、4个、5个 6个、7个、8个.根据分类加法计数原理,满足条件的两位数的 个数共有1+2+3+4+5+6+7+8=36
导航 解:方法一:按十位上的数字分别是1,2,3,4,5,6,7,8分成8类,在 每一类中满足条件的两位数分别有8个、7个、6个、5个、4 个、3个、2个、1个. 根据分类加法计数原理,满足条件的两位数的个数共有 8+7+6+5+4+3+2+1=36. 方法二:按个位上的数字分别是2,3,4,5,6,7,8,9分成8类,在每 一类中满足条件的两位数分别有1个、2个、3个、4个、5个、 6个、7个、8个.根据分类加法计数原理,满足条件的两位数的 个数共有1+2+3+4+5+6+7+8=36
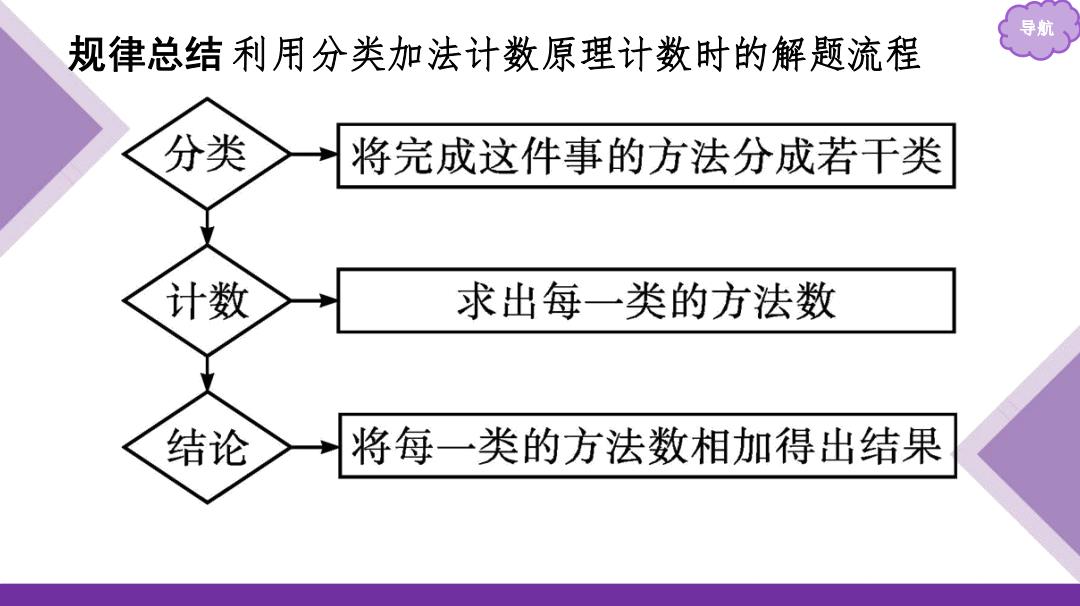
导航 规律总结利用分类加法计数原理计数时的解题流程 分类 将完成这件事的方法分成若干类 计数 求出每一类的方法数 结论 将每一类的方法数相加得出结果
导航 规律总结 利用分类加法计数原理计数时的解题流程