
全程设计 微专题一 两个计数原理与排列 组合的应用
微专题一 两个计数原理与排列、 组合的应用

两个计数原理的应用 1分类加法计数原理 任务 完成一件事 有两类不同方案,在第1类方案中有 分类 m种不同的方法,在第2类方案中有n 种不同的方法 计数 完成这件事共有N=m+n种不同的方法
一 两个计数原理的应用 1.分类加法计数原理
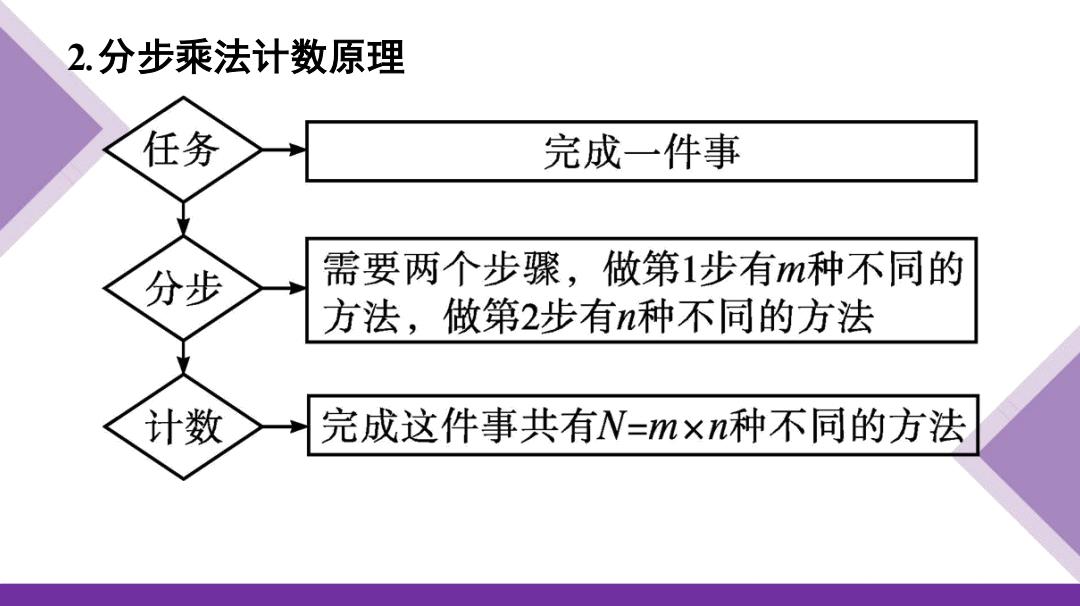
2.分步乘法计数原理 任务 完成一件事 分步 需要两个步骤,做第1步有m种不同的 方法,做第2步有n种不同的方法 计数 完成这件事共有N=m×n种不同的方法
2.分步乘法计数原理

命题角度1:“类中有步”的计数问题 【典型例题1】电视台在某节目中拿出两个信箱,其中存放 着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙 信箱中有20封,现由主持人抽奖确定幸运观众,若先确定一名 幸运之星,再从两信箱中各确定一名幸运伙伴,则有 种 不同的结果 答案:28800
命题角度1:“类中有步”的计数问题 【典型例题1】电视台在某节目中拿出两个信箱,其中存放 着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙 信箱中有20封,现由主持人抽奖确定幸运观众,若先确定一名 幸运之星,再从两信箱中各确定一名幸运伙伴,则有 种 不同的结果. 答案:28 800

解析:在甲箱或乙箱中抽取幸运之星,决定了后边选幸运伙 伴是不同的,故要分两类分别计算:第1类,幸运之星在甲箱中 抽,先确定幸运之星,再在两箱中各确定一名幸运伙伴,有 30X29×20=17400种结果;第2类,幸运之星在乙箱中抽,同理 有20×19×30=11400种结果, 因此共有17400+11400=28800种不同的结果
解析:在甲箱或乙箱中抽取幸运之星,决定了后边选幸运伙 伴是不同的,故要分两类分别计算:第1类,幸运之星在甲箱中 抽,先确定幸运之星,再在两箱中各确定一名幸运伙伴,有 30×29×20=17 400种结果;第2类,幸运之星在乙箱中抽,同理 有20×19×30=11 400种结果. 因此共有17 400+11 400=28 800种不同的结果