
全程设计 2.3.1 两条直线的交点坐标 2.3.2 两点间的距离公式
2.3.1 两条直线的交点坐标 2.3.2 两点间的距离公式

素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
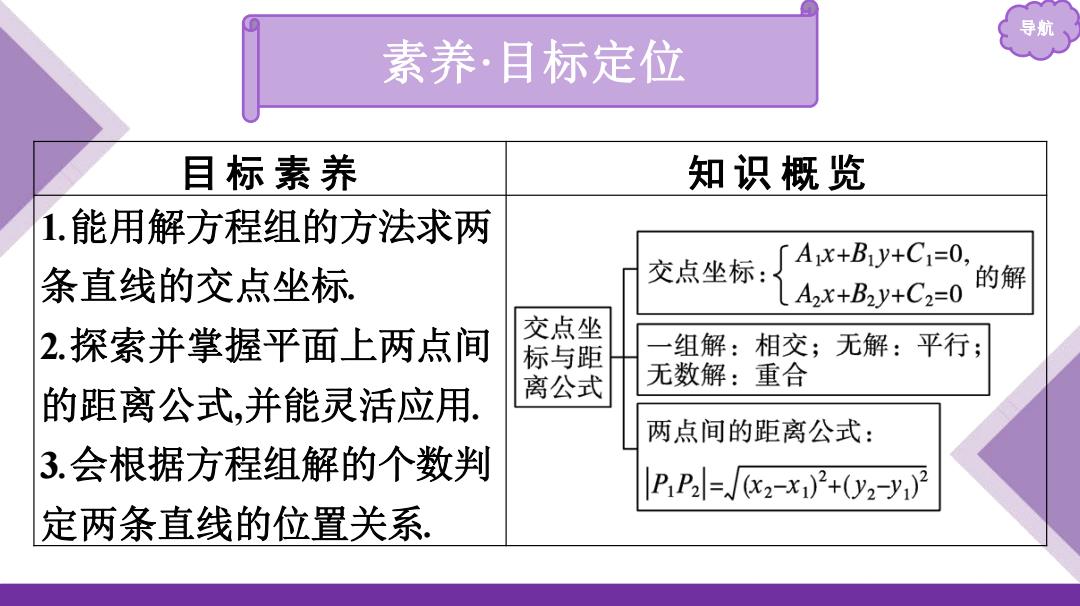
导航 素养·目标定位 目标素养 知识概览 1.能用解方程组的方法求两 条直线的交点坐标 交点坐标:厂Ax+By+C1=0, LA2x+B2y+C2=0 的解 2.探索并掌握平面上两点间 交点坐 标与距 组解:相交;无解:平行; 的距离公式,并能灵活应用. 离公式 无数解:重合 两点间的距离公式: 3.会根据方程组解的个数判 PP2l=02-x)2+(y2-y2 定两条直线的位置关系
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.能用解方程组的方法求两 条直线的交点坐标. 2.探索并掌握平面上两点间 的距离公式,并能灵活应用. 3.会根据方程组解的个数判 定两条直线的位置关系

导航 课前·基础认知 1,两条直线的交点坐标 1)两条直线的交点坐标 几何元素及关系 代数表示 点A A(a,b) 直线 1:Ax+By+C=0 点A在直线L上 直线,与的交点是4方程组+y十8:8的解是
导航 课前·基础认知 1.两条直线的交点坐标 (1)两条直线的交点坐标 几何元素及关系 代数表示 点A A(a,b) 直线l l:Ax+By+C=0 点A在直线l上 Aa+Bb+C=0 直线l1与l2的交点是A 方程组 𝐀𝟏 𝐱 + 𝐁𝟏 𝐲 + 𝐂𝟏 = 𝟎, 𝐀𝟐 𝐱 + 𝐁𝟐 𝐲 + 𝐂𝟐 = 𝟎 的解是 𝐱 = 𝐚, 𝐲 = 𝐛

导 微训练直线x+2y-2=0与直线2x+y-3=0的交点坐标是( A.(4,1) B.(1,4) c(传) D.(G勃 答案:C 解析:解方程组{ x+2y-2=0,得 4 即直线x+2y-2=0与 (2x+y-3=0, y 3, 直线2xt30的交点坐标是(传,)
导航 微训练直线x+2y-2=0与直线2x+y-3=0的交点坐标是( ) A.(4,1) B.(1,4) C. 𝟒 𝟑 , 𝟏 𝟑 D. 𝟏 𝟑 , 𝟒 𝟑 答案:C 解析:解方程组 𝒙 + 𝟐𝒚-𝟐 = 𝟎, 𝟐𝒙 + 𝒚-𝟑 = 𝟎, 得 𝒙 = 𝟒 𝟑 , 𝒚 = 𝟏 𝟑 , 即直线 x+2y-2=0 与 直线 2x+y-3=0 的交点坐标是 𝟒 𝟑 , 𝟏 𝟑