
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破
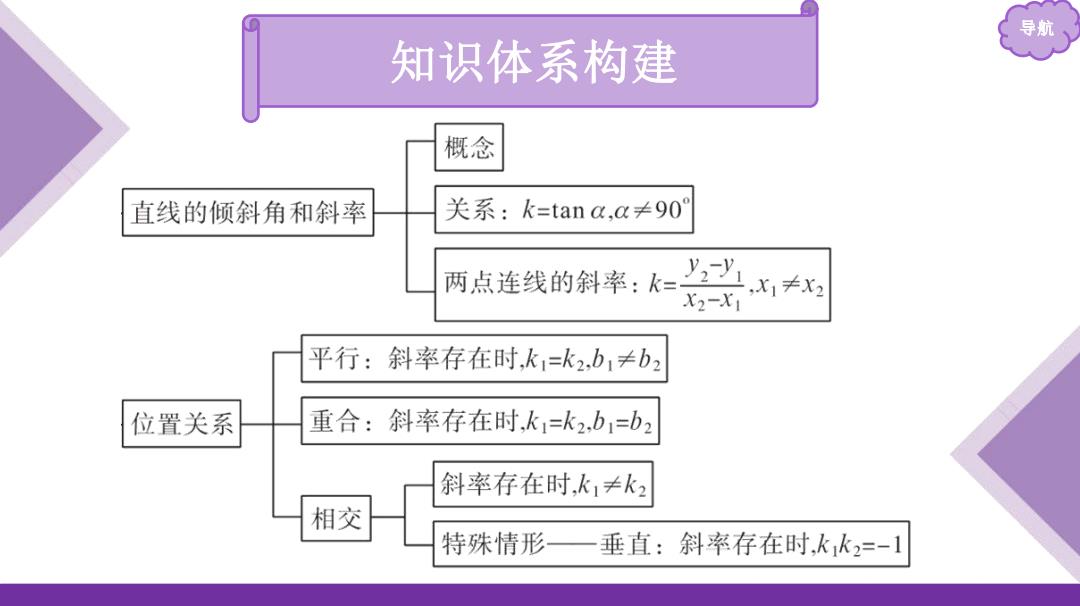
导航 知识体系构建 概念 直线的倾斜角和斜率 关系:k=tana,a≠90 两点连线的斜率:k= yy X2-X1 ,X1≠X2 平行:斜率存在时,k1=k2,b1≠b2 位置关系 重合:斜率存在时,k1=k2,b1=b2 斜率存在时,k1≠k2 相交 特殊情形 垂直:斜率存在时,kk2=-1
导航 知识体系构建

导航 点斜式:y-y=kx-x) 斜截式:y=kx+b 直线的方程 两点式: y-少1=-,x1≠x2yy2 y2-y1X2-1 费距式言+方1a≠0b学0 般式:Ax+By+C=0(其中A,B不同时为0) 两条直线的交点坐标:解方程组 两点间的距离:PP2=x2-x)2+y2y 距离 点到直线的距离:d=Axo+Byo+C (A,B不同时为0) JA2+B2 两条平行直线间的距离: |C-C2 (A,B不同时为0) JA2+B2
导航
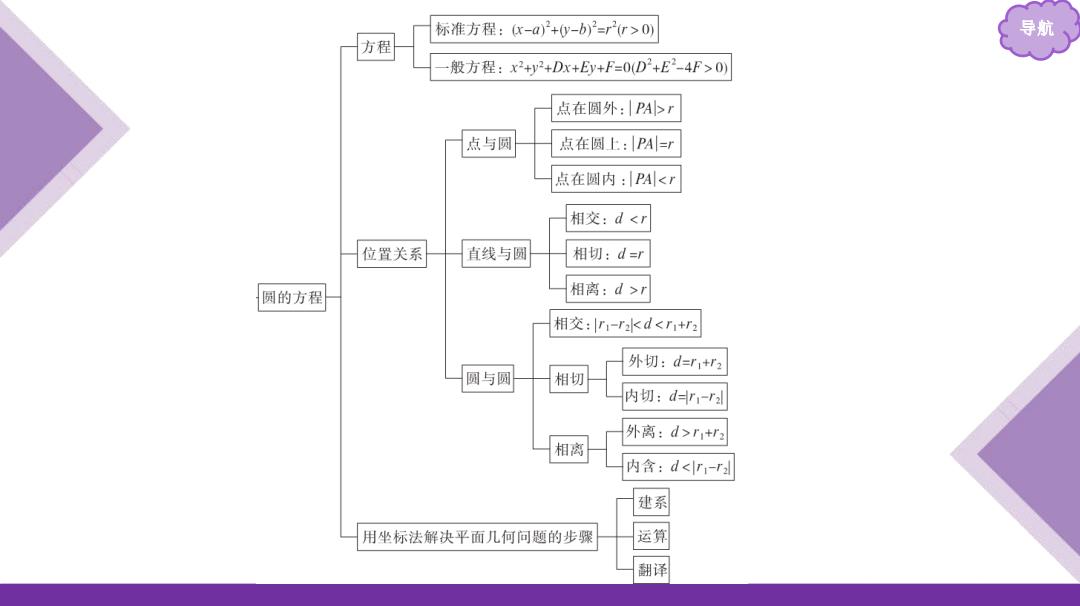
标准方程:c-a)+y-b)2=r2(r>0) 导航 方程 般方程:x2+y2+Dx+Ey+F=0(D+E2-4F>0) 点在圆外:|PA>r 点与圆 点在圆上:PA=T 点在圆内:PA<r 相交:d<r 位置关系 直线与圆 相切:d=r 圆的方程 相离:d>r 相交:r-rkd<r+r2 外切:d=r1+f2 圆与圆 相切 内切:d=r-r 外离:d>r+r2 相离 内含:d<r-r 建系 用坐标法解决平面几何问题的步骤 运算 翻译
导航