
代入初始条件得到的矩阵方程 y(0)=C1+C2+…+Cn=y0 y'(0)=PC+p2C2+.+pC DyO y"-(0)=pm-C,+p2m-C2+…+pm-Cn=D(n-1)y0 初始条件数应该和常数数相等,由此构成一个确定C1,.,C的线性代 数方程组,写成: P P2 C2 Dy0 V.C=DYO p D(n-1)y0 矩阵V由特征根向量p确定,这种矩阵称为范德蒙特矩阵。在 MATLAB中,有生成它的函数vander(p)
代入初始条件得到的矩阵方程 初始条件数应该和常数数相等,由此构成一个确定C1 ,…,Cn的线性代 数方程组,写成: 矩阵V由特征根向量p确定,这种矩阵称为范德蒙特矩阵。在 MATLAB中,有生成它的函数vander(p)。 1 2 1 1 2 2 ( 1) ( 1) ( 1) ( 1) 1 1 2 2 (0) 0 '(0) 0 (0) ( 1) 0 n n n n n n n n n y C C C y y p C p C p C Dy y p C p C p C D n y − − − − = + + + = = + + + = = + + + = − 1 2 1 1 2 2 1 1 1 1 1 1 0 0 ' ( 1) 0 n n n n n n C y p p p C Dy p p p C D n y − − − = − V C = DY0

求零输入响应程序eXn913 它产生的矩阵与上述矩阵排列转了90度,故用 V=rot90(vander(p),按此思路编成程序exn913: a=input('输入分母系数向量a=[a1,a2,.·.]='); n=length (a)-1; Y0=input('初始条件Y0=[y0,Dy0,D2y0,·..]='); p=roots(a);V=rot90(vander(p));生成系数矩阵v c=V\Y0‘; 号用左除求出系数向量C 号以下是计算并画出时间响应的程序段 dt=input ('dt=');tf=input ('tf=' 号生成t向量和y初始向量 t=0:dt:tf;y=zeros(1,length (t)); for k=1:n y=y+c(k)*exp(p(k)*t);end plot(t,y),grid 号绘图
求零输入响应程序exn913 它产生的矩阵与上述矩阵排列转了90度,故用 V=rot90(vander(p)),按此思路编成程序exn913: a=input('输入分母系数向量a=[a1,a2,...]= '); n=length(a)-1; Y0=input('初始条件 Y0=[y0,Dy0,D2y0,...]= '); p=roots(a); V=rot90(vander(p));%生成系数矩阵V c= V\Y0‘ ; % 用左除求出系数向量C % 以下是计算并画出时间响应的程序段 dt=input('dt='); tf=input('tf= ') % 生成t向量和y初始向量 t=0:dt:tf; y=zeros(1,length(t)); for k=1:n y= y+c(k)*exp(p(k)*t);end plot(t,y),grid % 绘图
数字实例 用这一个普遍程序来解一个三阶系统,设其微分方程为: +24-y+9+3y=0 din dtu-1 dt 初始条件为:y(0)=1,y'(0)=0,y"(0)=0,求零输入响应。 解:运行exn913,按提示输入 a为[1,2,9,3];Y0为[1,0,0];dt为 0.8 0.1;f为5;即可得到t=0~5秒 Y0[1,0,0] 的零输入响应曲线。 0.6 0.4 0=0,,0明 再分别取Y0为[0,1,0]: [0,0,1],用hold on语句使三次 0.2 011 运行生成的图形叠画在一幅图 上,得到右图
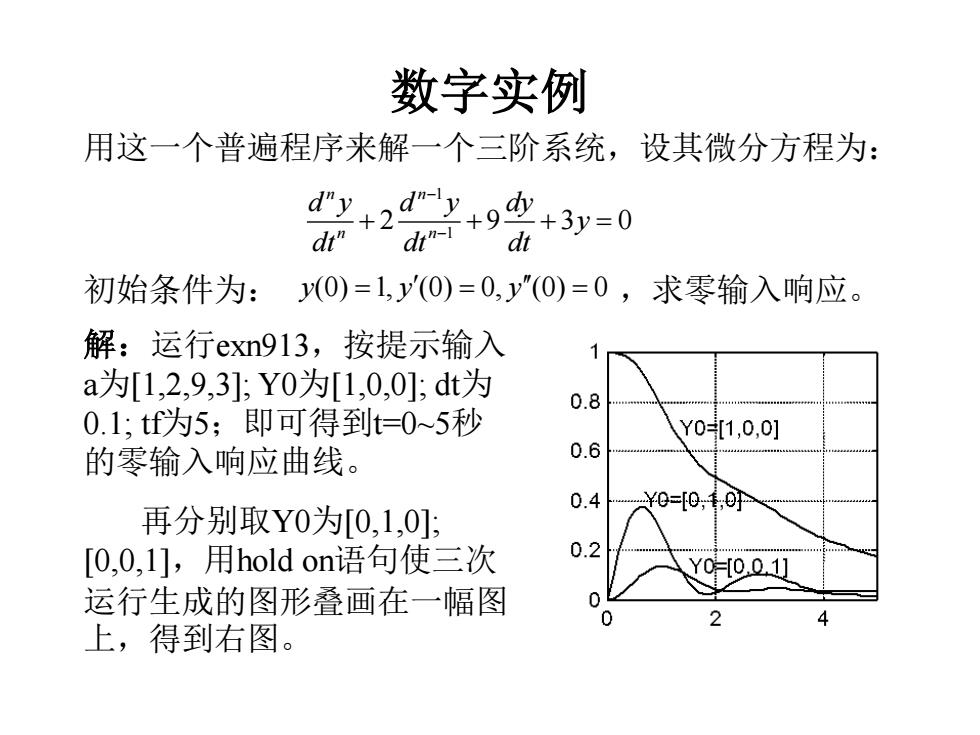
数字实例 用这一个普遍程序来解一个三阶系统,设其微分方程为: 初始条件为: ,求零输入响应。 1 1 2 9 3 0 n n n n d y d y dy y dt dt dt − − + + + = y y y (0) 1, (0) 0, (0) 0 = = = 解:运行exn913,按提示输入 a为[1,2,9,3]; Y0为[1,0,0]; dt为 0.1; tf为5;即可得到t=0~5秒 的零输入响应曲线。 再分别取Y0为[0,1,0]; [0,0,1],用hold on语句使三次 运行生成的图形叠画在一幅图 上,得到右图

例9-1-4重极点求反变换 命题:n级放大器,每级的转移函数均为H(s)= (s+0) 求阶跃输入下的过渡过程,画出不同时的波形及频率特性。 ·解:◆建模系统的转移函数为H(S)=,阶跃输入的拉普拉 斯变换为1/s,因此输出为两者的乘积,即 Y(s)= @j (S+0)” 求Y(s)的拉普拉斯反变换,即可得到输出过渡过程y()。这里 我们遇到了一个有多重极点-wn的H(s)求拉普拉斯反变换 的问题,数学上比较麻烦。为了避开重极点问题,可以有 意把极点拉开一些,例如设n个极点散布在-0.98wn到 1.02wn之间,由此就可用下面的程序来求:
例9-1-4 重极点求反变换 命题:n级放大器,每级的转移函数均为 , 求阶跃输入下的过渡过程,画出n不同时的波形及频率特性。 • 解:◆建模 系统的转移函数为H(s)=,阶跃输入的拉普拉 斯变换为1/ s,因此 输出为两者的乘积,即 求Y(s)的拉普拉斯反变换,即可得到输出过渡过程y(t)。这里 我们遇到了一个有多重极点-wn的H(s)求拉普拉斯反变换 的问题,数学上比较麻烦。为了避开重极点问题,可以有 意把极点拉开一些,例如设n个极点散布在-0.98wn到 1.02wn之间,由此就可用下面的程序来求: 0 0 ( ) ( ) H s s = + 0 0 ( ) ( ) n n Y s s s = +

程序exn914(1) clear,clf,N=input('输入放大器级数N=); wn=1000;dt=1e-4;tf=0.01;t=0:dt:tf; y=zeros(N,length(t)); %输出初始化 for n=1:N p0=--linspace(.95,1.05,n)*wn;%将H(s)极点分散布置 ay=poly(Ip0,O]);%由Y(s)的极点求分母系数 by prod(abs(po)); %求Y(s)的分子系数 [r,p]residue(by,ay); %求Y(s)的留数极点 for k=1:n+1 %把各时域分量相加 y(n,:)=y(n,:)+r(k)"exp(p(k)*t); end figure(1),plot(t,y(n,:));grid,hold on %绘制过渡过程 end
程序exn914(1) clear,clf, N=input('输入放大器级数N='); wn=1000; dt=1e-4; tf=0.01;t = 0:dt:tf; y=zeros(N,length(t)); % 输出初始化 for n=1:N p0=-linspace(.95,1.05,n)*wn; % 将H(s)极点分散布置 ay = poly([p0,0]); % 由Y(s)的极点求分母系数 by = prod(abs(p0)); % 求Y(s)的分子系数 [r,p] = residue(by,ay); % 求Y(s)的留数极点 for k = 1: n+1 % 把各时域分量相加 y(n,:) = y(n,:) + r(k)*exp(p(k)*t); end figure(1),plot(t, y(n,: ));grid,hold on % 绘制过渡过程 end