
例9-1-2 线性系统冲击响应 。 编写求任意高阶连续常系数线性系统冲击响应的程序。 ·解:◆建模这个问题在第四章介绍多项式函数库时已打下 了基础,在第七章例7-3-1中又给出了解法,读者可先看 懂那些内容,然后再看本题。任意阶次的连续线性系统可 用下列微分方程表述: d"y dy d"u a- at at a+ at ·写成传递函数形式为 H(s)= Y(s)_bs"+b2sm+…+bns+bmtl Js)as”+a42sn-+…+ans+al ·其特性可用系统传递函数的分子分母系数向量b和a来表示
例9-1-2 线性系统冲击响应 • 编写求任意高阶连续常系数线性系统冲击响应的程序。 • 解:◆建模 这个问题在第四章介绍多项式函数库时已打下 了基础,在第七章例7-3-1中又给出了解法,读者可先看 懂那些内容,然后再看本题。任意阶次的连续线性系统可 用下列微分方程表述: • 写成传递函数形式为 • 其特性可用系统传递函数的分子分母系数向量b和a来表示。 1 1 2 1 1 1 n n m n m n n m m d y d y dy d u du a a a a y b b b u at at at at at − + + + + = + + + + + 1 1 2 1 1 1 2 1 ( ) ( ) ( ) m m m m n n n n Y s b s b s b s b H s U s a s a s a s a − + − + + + + + = = + + + +

传递函数反变换的求法 如果分母系数多项式没有重根,则可以把两个多项式 之比分解成个一阶部分分式之和。即: Hs)=5+5++h s-P s-P2 s-P 其中p1,p2,pn是分母多项式的n个根,而r1,r2,,rm 是则对应于这个根的留数。一阶分式的反变换可以查表 得到,容易写出冲击响应的公式如下: h(t)=re+5e+…+r,ew 可见只要求出根向量p和留数向量r,线性方程的解就 得到了。求根是代数问题,当阶次很高时,代数方程没有 解析解。可喜的是MATLAB提供了用数值方法求根和留数 的函数residue.m,它的调用格式为: [r,p]=residue(b,a)
传递函数反变换的求法 • 如果分母系数多项式没有重根,则可以把两个多项式 之比分解成n个一阶部分分式之和。即: • 其中p1,p2,…,pn是分母多项式的n个根,而r1,r2,…,rn 是则对应于这n个根的留数。一阶分式的反变换可以查表 得到,容易写出冲击响应的公式如下: • 可见只要求出根向量p和留数向量r,线性方程的解就 得到了。求根是代数问题,当阶次很高时,代数方程没有 解析解。可喜的是MATLAB提供了用数值方法求根和留数 的函数residue.m,它的调用格式为: • [r,p]=residue(b,a) 1 2 1 2 ( ) n n r r r H s s p s p s p = + + + − − − 1 2 1 2 ( ) n p t p t p t n h t r e r e r e = + + +

程序exn912 a=input('分母系数向量a=(书上取poly([0,-1,-2,-5]))) b=input((分子系数向量b=(书上取[1,7,1])) [r,p]residue(b,a), %求留数 k=input(是否要求波形?是,键入1;否,键入0); if k==1 dt=input('dt=(书上取0.05)); tf=input('tf=(书上取5);%设定时间数组 t=0:dt:tf;h=zeros(1,length(t)); %h的初始化 for i=1:length(a)-1 %根数为a的长度减1 h=h+r()*ep(p(*t);%叠加各根分量 end,plot(t,h),grid else,end
程序exn912 a=input('分母系数向量a=(书上取 poly([0,-1,-2,-5]) ) ') b=input('分子系数向量b=(书上取 [1,7,1] ) ') [r,p] = residue( b, a), % 求留数 k=input('是否要求波形?是,键入1;否,键入0 '); if k==1 dt=input('dt=(书上取0.05) '); tf=input('tf=(书上取5 '); %设定时间数组 t=0:dt:tf;h=zeros(1,length(t)); % h的初始化 for i=1:length(a)-1 % 根数为a的长度减1 h = h+ r(i)*exp(p(i)*t); % 叠加各根分量 end, plot(t,h),grid else,end
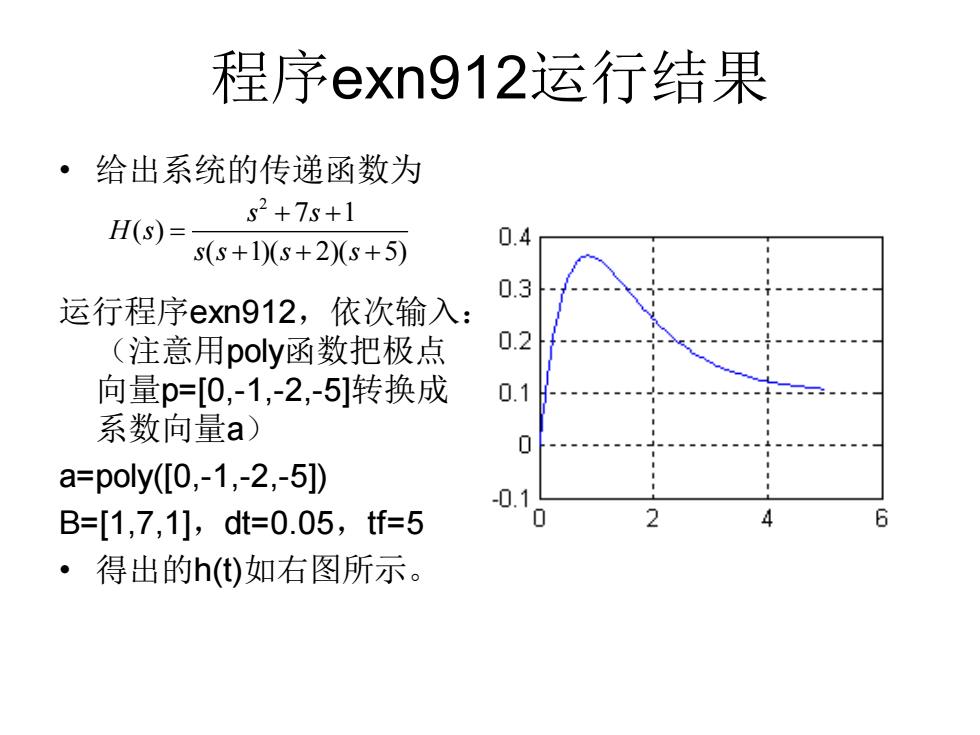
程序exn912运行结果 ·给出系统的传递函数为 s2+7s+1 H(s)= s(s+1)(s+2)(s+5) 0.4 0.3 运行程序en912,依次输入: (注意用poly函数把极点 0.2 向量p=[0,-1,-2,-5]转换成 0.1 系数向量a) 0 a=poly([0,-1,-2,-5]) -0.1 B=[1,7,1],dt=0.05,tf=5 ·得出的h(t)如右图所示
程序exn912运行结果 • 给出系统的传递函数为 运行程序exn912,依次输入: (注意用poly函数把极点 向量p=[0,-1,-2,-5]转换成 系数向量a) a=poly([0,-1,-2,-5]) B=[1,7,1],dt=0.05,tf=5 • 得出的h(t)如右图所示。 2 7 1 ( ) ( 1)( 2)( 5) s s H s s s s s + + = + + +

9-1-3线性系统零输入响应的计算 线性时不变连续系统的特性可用常微分方程表示为: d-y du bou (n≥m) 求其零输入响应。 解:在零输入条件u=0时,等式右端为零。系统响应的通 解为: y(t)=Cem+Ces+..+Cev 其中,p是特征方程的n个根组成的向量p1,P2…,pn],其 每个分量的系数C则由y及其各阶导数的初始条件y0, Dy0,..,D(n-1)y0来确定
9-1-3 线性系统零输入响应的计算 线性时不变连续系统的特性可用常微分方程表示为: 求其零输入响应。 解:在零输入条件u=0时,等式右端为零。系统响应的通 解为: 其中,p是特征方程的n个根组成的向量[p1 ,p2 ,…,pn ],其 每个分量的系数Cn则由y及其各阶导数的初始条件y0, Dy0, …, D(n-1)y0来确定。 1 1 1 1 0 1 ( ) n n m n n m d y d y dy d u du a a a y b b b u n m dt dt dt dt dt − − − + + + + = + + + 1 2 1 2 ( ) n p t p t p t n y t C e C e C e = + + +