
Q(x) = b. (x-a).(x2 + px + q)".. (p2 - 4q < 0)2个常数待定P(x)A2一Q(x)ax一ax-Mx+NM.x+N+(x? + px+g)u-+ +(x2 + px+g) uM.x+N2u个常数待定?x+px+q其中诸A,M,,N,都是常数可由待定系数法确定P(x)的部分分式(最简分式)式中每个分式叫做Q(x)
= ( ) ( ) Q x P x 其中诸 , , 都是常数, Ai Mi Ni 可由待定系数法确定, 式中每个分式叫做 的 ( ) ( ) Q x P x + ( − ) 1 x a A 部分分式(最简分式). ( ) ( ) ( ) , 2 Q x = b0 x − a x + px + q ( 4 0) 2 p − q + ( − ) 2 x a A + x − a + + + + + 2 −1 2 2 ( ) x px q M x N + + + + + + x px q M x N 2 −1 A 1 ( ) + ( + + ) 2 x px q M1 x + N1 个常数待定 2个常数待定

用此定理有理函数的积分就易计算了耳由下面的例题可看出:有理函数的积分是初等函数注系数的确定,一般有三种方法(1)等式两边同次幂系数相等:(2) 赋值;(3)求导与赋值结合使用
用此定理有理函数的积分就易计算了. 且由下面的例题可看出: 有理函数的积分是初等函数. 注 系数的确定,一般有三种方法: (1) 等式两边同次幂系数相等; (2) 赋值; (3) 求导与赋值结合使用

假分式x+x+例1 求dxx2 +1解由多项式除法,有x3+x+11=x+x? +1x? +12dx原式={xdx++ arctan x + C2+1说明:当被积函数是假分式时,应把它分为个多项式和一个真分式,分别积分
例1 求 x x x x d 1 1 2 3 + + + 解 由多项式除法,有 = + + + 1 1 2 3 x x x + = + 1 d d 2 x x 原式 x x x C x = + arctan + 2 2 说明:当被积函数是假分式时,应把它分为 一个多项式和一个真分式,分别积分. 1 1 2 + + x x 假分式

x+3例2 求dx.22-5x+6xABx+3x+3解x-3x-5x+6x-2(x -2)(x-3)因式分解 x+3= A(x-3)+ B(x-2)x+3=(A+B)x-(3A+2B)比较系数A+B=1A=-5B=6-(3A+2B)=3,6-5x+3x2-5x+6x-2x-3
− + + x x x x d 5 6 3 例 2 2 求 5 6 3 2 − + + x x x ( 2)( 3 ) 3 − − + = x x x + − = x 2 A x + 3 = A ( x − 3 ) + B ( x − 2 ) x + 3 = ( A + B ) x − ( 3 A + 2 B ) − + = + = (3 2 ) 3, 1, A B A B == − 6 5 BA 5 6 3 2 − + + x x x 解 3 6 25 − + −− = x x x − 3 B 比较系数 因式分解
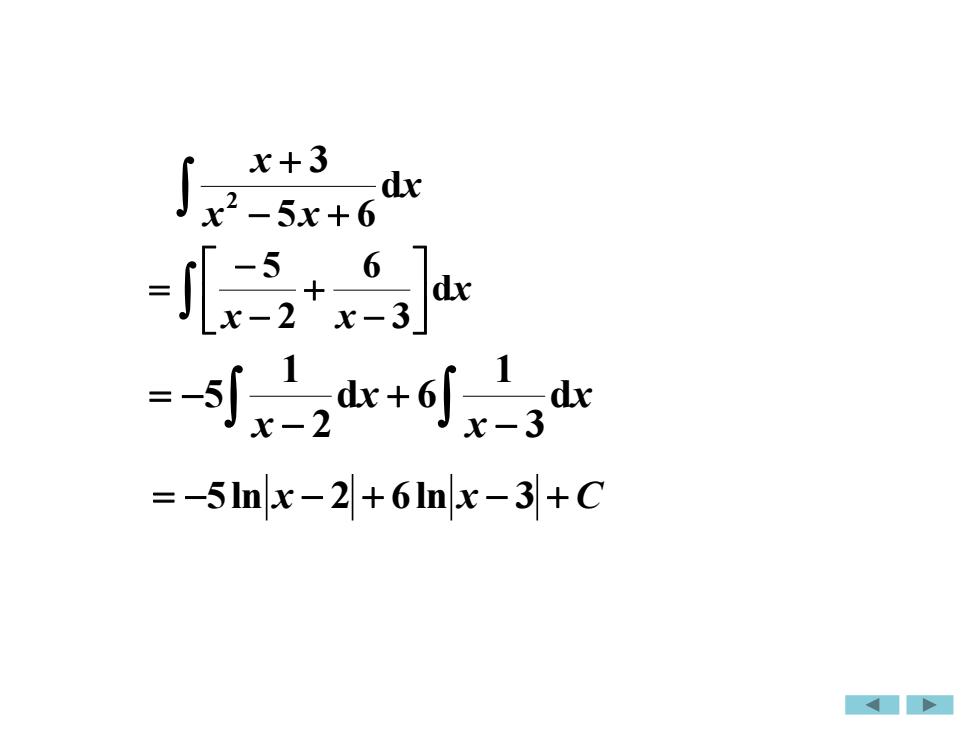
x+3dx25x +656dx2Xdxdxx-2x-3= -5ln|x -2|+6lnx-3+C
− + + x x x x d 5 6 3 2 − + − = − x x x x d 3 1 d 6 2 1 5 x x x d 3 6 2 5 − + − − = = −5ln x − 2 + 6ln x − 3 + C