
二、向量的线性运算1,向量的加法2.向量的减法3.向量与数的乘法
二、向量的线性运算 1.向量的加法 2.向量的减法 3.向量与数的乘法
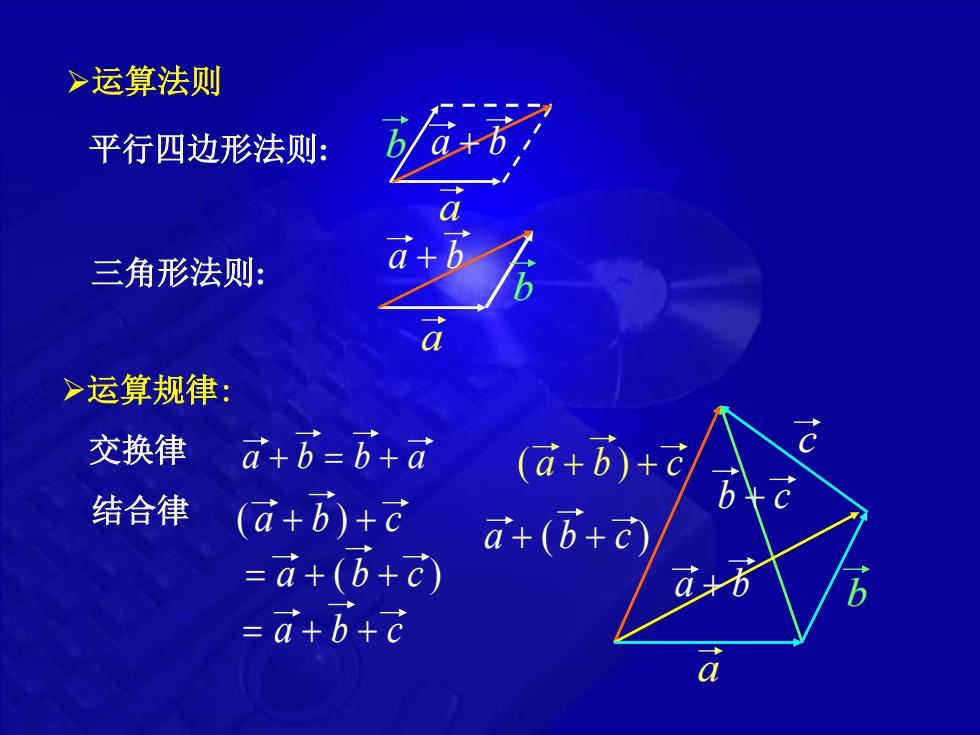
>运算法则平行四边形法则:+三角形法则:a>运算规律:C交换律a+b=-b+a(a+b)+b5XC结合律(a+b)+ta+(b+t)=a+(b+c)a+bb=a+b+ca
三角形法则: 平行四边形法则: 运算规律: 交换律 结合律 b b a b b a ( a b ) c a ( b c ) a b c a b c a b b c a ( b c ) ( a b ) c a a a b a b 运算法则

注三角形法则可推广到多个向量相加s= a +az +a, + ay +asaa2Sa
s a3 a4 a5 a2 a1 1 2 3 4 5 s a a a a a 注 三角形法则可推广到多个向量相加

>运算法则三角形法则:b-ob-a-b+(-a)特别当b=a时,有a-a=a+(-a)=0>运算规律:三角不等式a+b|≤||+b][a-b|≤|a|+|b
三角不等式 特别当b a 时,有 a 运算法则 三角形法则: 运算规律:

>运算法则是一个数,与的乘积是一个向量,记作ar>0时,a与a同向,,aa=a;规定4<o时,a与a反向,「a=-a=0时,a=0[a=a·注若a0,则一a为单位向量,记作é>运算律结合律(ua)=μ(aa)=aμua分配律(a+μ)a=aa+μaa(a+b)=aa+ab
a a 是一个数 , a . 规定 运算律 结合律 ( a) ( a) a 分配律 (a b ) a b 运算法则 注 1 a 则 a 为单位向量,记作 a e 与 a 的乘积是一个向量, 记作