
数学建模与数学实验 拟合
数学建模与数学实验 拟 合

实验目的 1.直观了解拟合基本内容. 2.掌握用数学软件求解拟合问题. 实验内容 1.拟合问题引例及基本原理. 2.用数学软件求解拟合问题. 3.应用实例. 4.实验作业
实验目的 实验内容 2. 掌握用数学软件求解拟合问题. 1. 直观了解拟合基本内容. 1. 拟合问题引例及基本原理. 4. 实验作业. 2. 用数学软件求解拟合问题. 3. 应用实例

拟合 1.拟合问题引例 2.拟合的基本原理
拟 合 2. 拟合的基本原理 1. 拟合问题引例
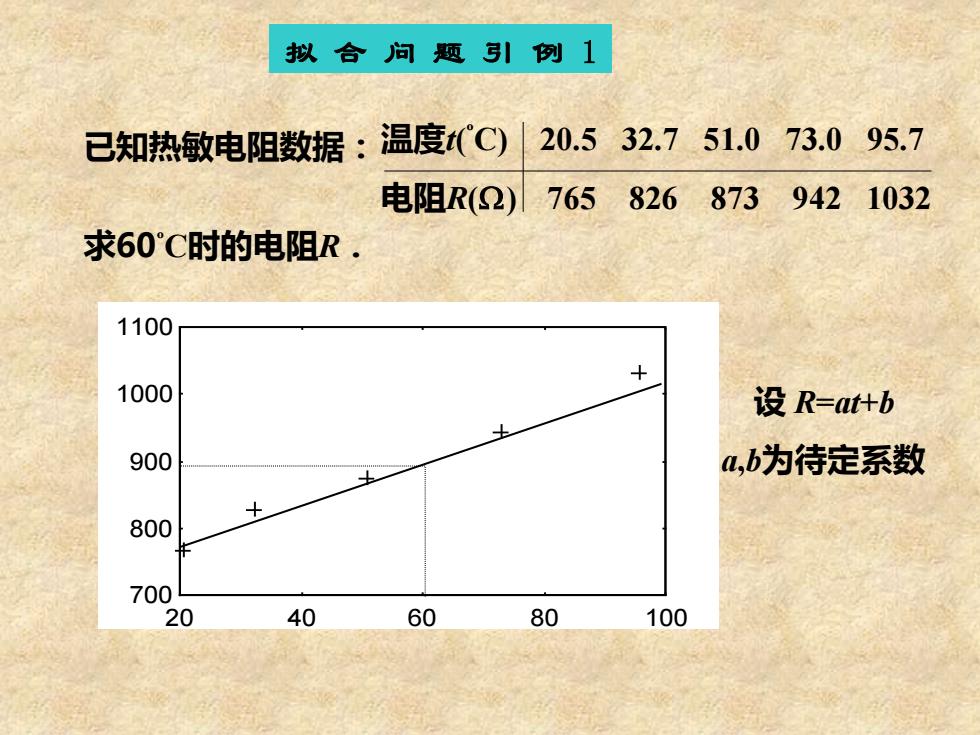
拟合问题3引例1 己知热敏电阻数据:温度(C) 20.532.751.073.095.7 电阻R(2)7658268739421032 求60°C时的电阻R. 1100 1000 设R=t+b 900 ,b为待定系数 800 700 20 40 60 80 100
拟 合 问 题 引 例 1 温度t( ºC) 20.5 32.7 51.0 73.0 95.7 电阻R() 765 826 873 942 1032 已知热敏电阻数据: 求60ºC时的电阻R. 20 40 60 80 100 700 800 900 1000 1100 设 R=at+b a,b为待定系数
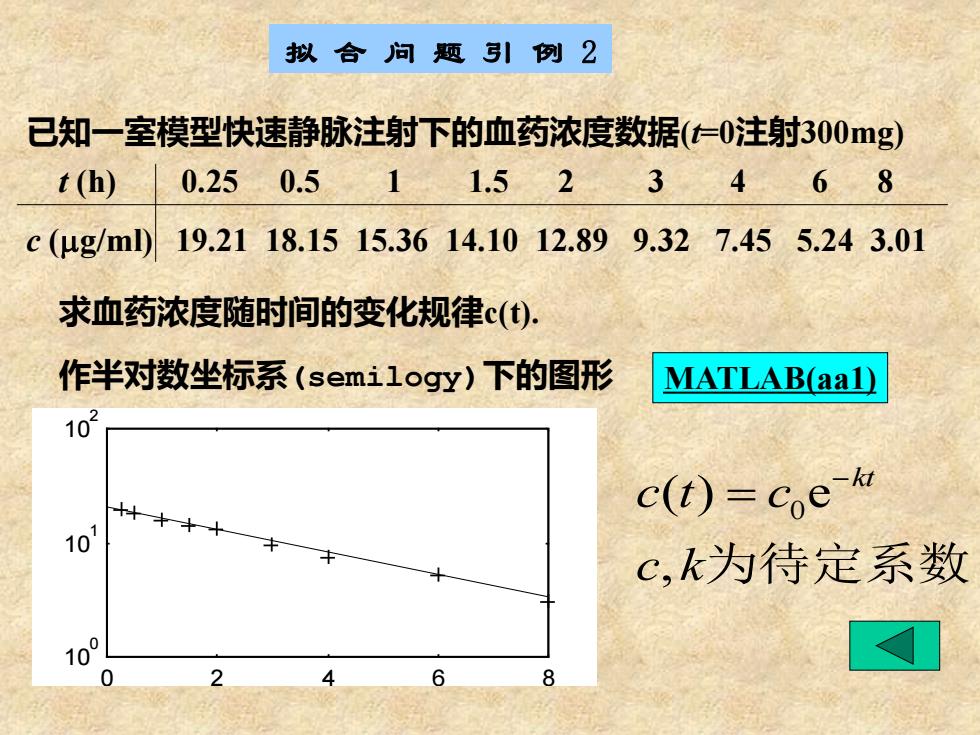
拟合问题引例2 已知一室模型快速静脉注射下的血药浓度数据(=0注射300mg) t(h) 0.250.511.523468 c(μgml019.2118.1515.3614.1012.899.327.455.243.01 求血药浓度随时间的变化规律c(). 作半对数坐标系(semilogy)下的图形 MATLAB(aa1) 103 c(t)=coe-k 10 c,k为待定系数 100 0 2 6 8
拟 合 问 题 引 例 2 t (h) 0.25 0.5 1 1.5 2 3 4 6 8 c (g/ml) 19.21 18.15 15.36 14.10 12.89 9.32 7.45 5.24 3.01 已知一室模型快速静脉注射下的血药浓度数据(t=0注射300mg) 求血药浓度随时间的变化规律c(t). 作半对数坐标系(semilogy)下的图形 0 ( ) e , kt c t c c k − = 为待定系数 0 2 4 6 8 100 101 102 MATLAB(aa1)