
线性代数教程第0503节相似矩阵 2347 利用对角矩阵计算矩阵多项式 若A=PBP,则 k个 APBP PBP-.PEP-PBPD PBP-. A的多项式 (A)=a0A"+aiA++anA+arE ao P B"P+aP B"-P+. an-PBP+an PE P- P(ao B"+aiB"++anB+ar E)P Po(B)P. 线性代数小组 第6页
线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第6页 利用对角矩阵计算矩阵多项式 , 1 A PB P − 若 = a PB P a PE P a P B P a P B P n n n n 1 1 1 1 1 1 1 0 − − − − − − + + = + + A = k A的多项式 A a A a A an A anE n n = + + + − + − 1 1 0 1 ( ) ( ) . 1 P B P − = . 1 P B P k − = 则 P a B a B an B anE P n n 1 1 1 0 1 ( ) − − − = + ++ + PBP −1 PBP −1 PBP −1 PBP −1 k个
线性代数教程第0503节相似矩阵 2347 特别地,若可逆矩阵P使P1AP=人为对角矩阵, 则 A=P人P-,P(A)=Pp(A)P 对于对角矩阵私,有 1所 2经 利用上 述结论可以 p(2) 很方便地计 p(2) 算矩阵A的 p(A)= 多项式p(A) p() 线性代数小组 第页
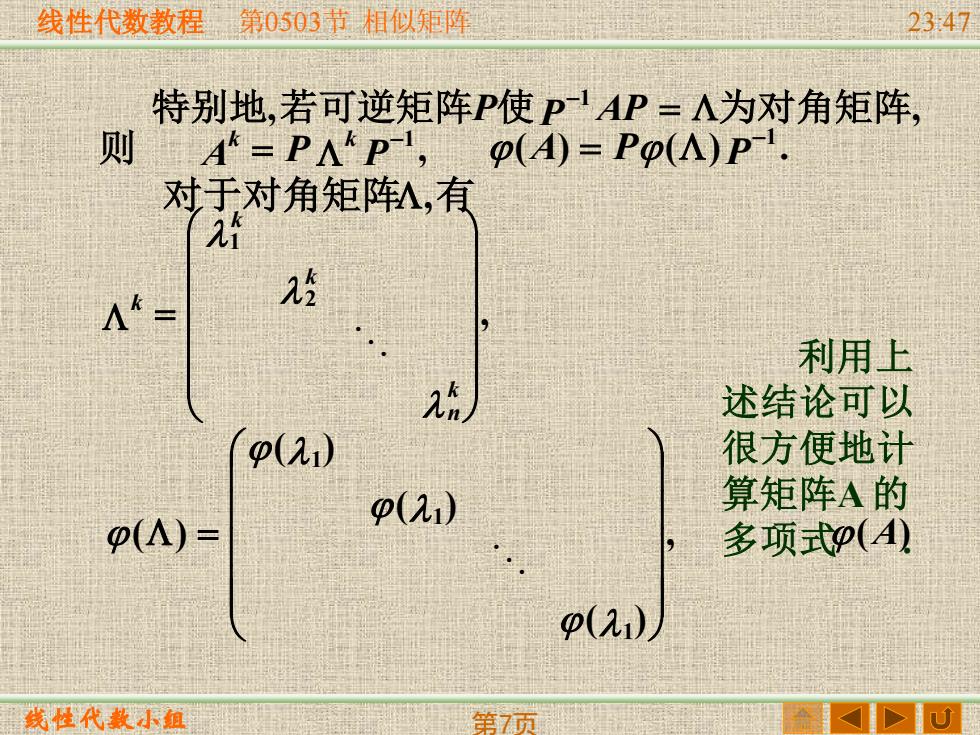
线性代数教程 线性代数小组 第0503节 相似矩阵 23:47 第7页 , , 特别地 若可逆矩阵P使P −1 AP = 为对角矩阵 , 1 A P P k k − 则 = ( ) ( ) . 1 A P P − = 对于对角矩阵,有 , 2 1 = k n k k k , ( ) ( ) ( ) ( ) 1 1 1 = 利用上 述结论可以 很方便地计 算矩阵A 的 多项式 . (A)