
(二)系统结构图的建立 建立系统的结构图,其步骤如下: (1)建立控制系统各元部件的微分方程。 (2)对各元件的微分方程进行拉氏变换,并作出各元件的 结构图。 (3)按系统中各变量的传递顺序,依次将各元件的结构图 连接起来,置系统的输入变量于左端,输出变量于右端, 便得到系统的结构图。 例2.1试绘制图2-20所示无源网络的结构图
(二)系统结构图的建立 建立系统的结构图,其步骤如下: (1)建立控制系统各元部件的微分方程。 (2)对各元件的微分方程进行拉氏变换,并作出各元件的 结构图。 (3)按系统中各变量的传递顺序,依次将各元件的结构图 连接起来,置系统的输入变量于左端,输出变量于右端, 便得到系统的结构图。 例2.1 试绘制图2-20所示无源网络的结构图
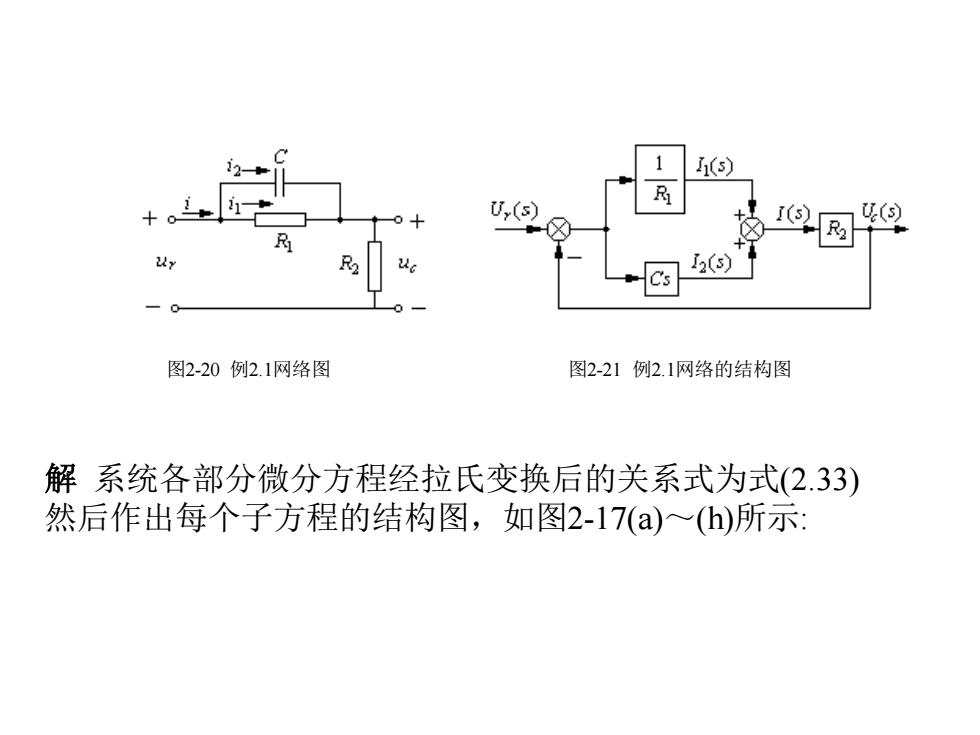
1 (s) U,(s) (5) 图2-20例2.1网络图 图2-21例2.1网络的结构图 解系统各部分微分方程经拉氏变换后的关系式为式(2.33) 然后作出每个子方程的结构图,如图2-17(a)~(h)所示:
解 系统各部分微分方程经拉氏变换后的关系式为式(2.33) 然后作出每个子方程的结构图,如图2-17(a)~(h)所示: 图2-20 例2.1网络图 图2-21 例2.1网络的结构图
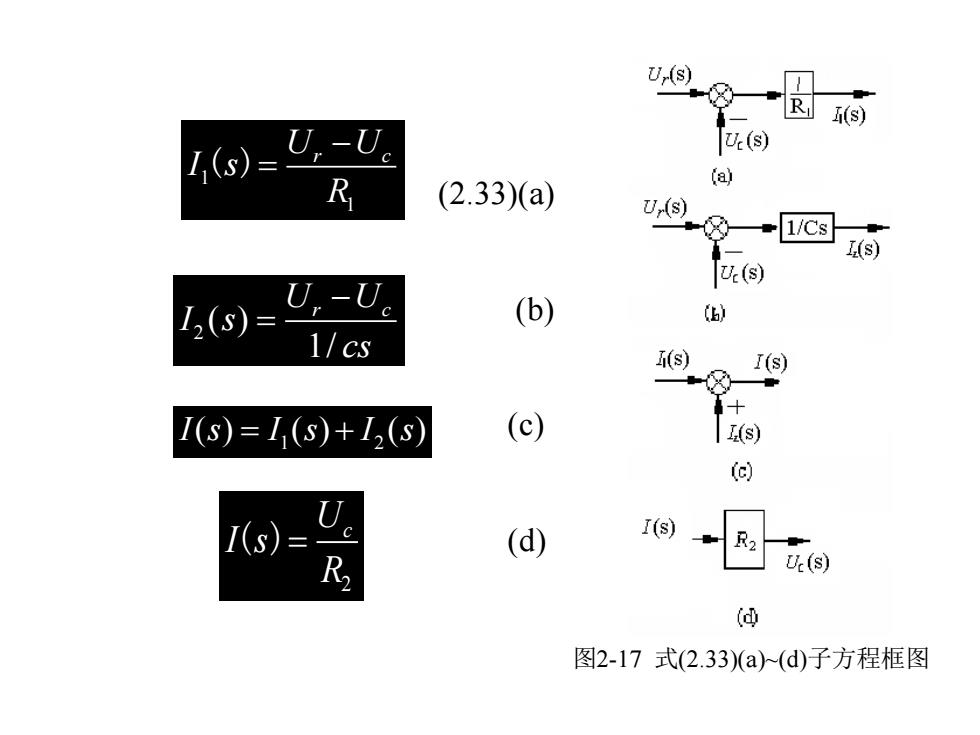
U(母) R (s) I(s)= U.-U (s) R a (2.33)(a) U() 1/Cs I(s) U.(s) I2(s)= U.-U. (b) 6) 1/cs I(s) I(s) I(s)=I(S)+I2(S) (c) d I(s) (d) I(s) R (S) (画 图2-17式(2.33)a(d)子方程框图
2 Uc I s R ( )= 2 ( ) 1 / U U r c I s cs − = (2.33)(a) (b) (c) (d) 图2-17 式(2.33)(a)~(d)子方程框图 1 2 I s I s I s ( ) ( ) ( ) = + 1 1 U U r c I s R − ( )=
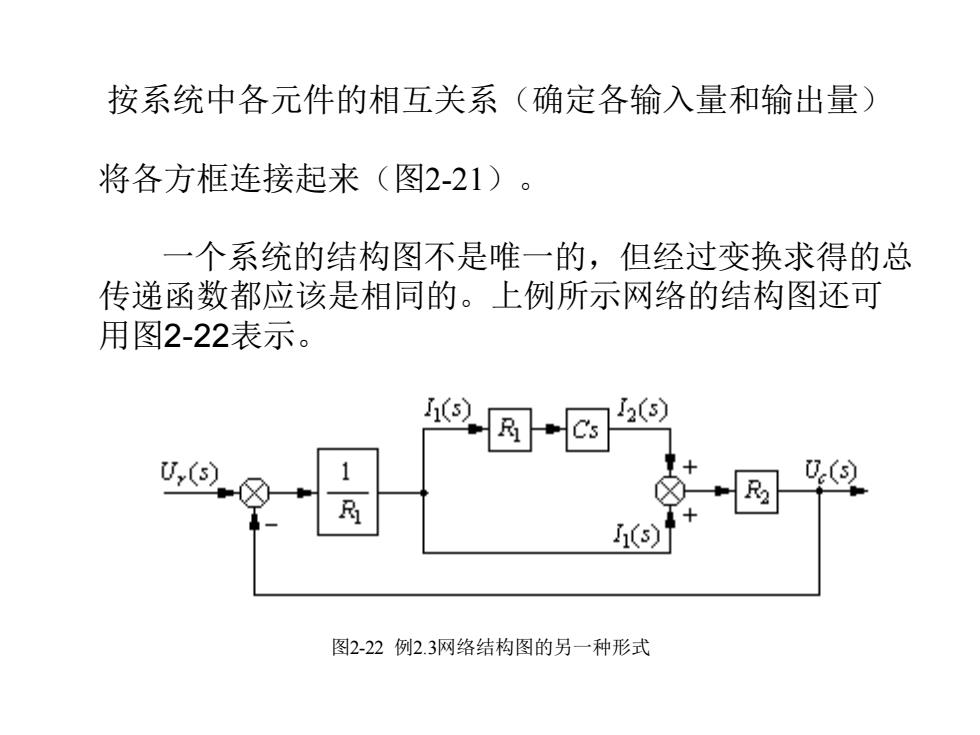
按系统中各元件的相互关系(确定各输入量和输出量) 将各方框连接起来(图2-21)。 一个系统的结构图不是唯一的,但经过变换求得的总 传递函数都应该是相同的。上例所示网络的结构图还可 用图2-22表示。 风s 2(s) U,(s) h(s) 图2-22例2.3网络结构图的另一种形式
按系统中各元件的相互关系(确定各输入量和输出量) 将各方框连接起来(图2-21)。 一个系统的结构图不是唯一的,但经过变换求得的总 传递函数都应该是相同的。上例所示网络的结构图还可 用图2-22表示。 图2-22 例2.3网络结构图的另一种形式

(三)结构图的等效变换 结构图的运算和变换,就是将结构图化为一个等效的 方框,使方框中的数学表达式为等效传递函数。 结构图的变换应按等效原理进行。 1.结构图的基本组成形式 (1)串联连接:方框与方框首尾相连。前一个方框的 输出,作为后一个方框的输入。 (2)并联连接:两个或多个方框,输入相同,输出为 各方框输出的代数和。 (3)反馈连接:一个方框的输出,输入到另一个方框, 得到的输出再返回作用于前一个方框的 输入端。如图2-37所示
(三)结构图的等效变换 结构图的运算和变换,就是将结构图化为一个等效的 方框,使方框中的数学表达式为等效传递函数。 结构图的变换应按等效原理进行。 1.结构图的基本组成形式 (1)串联连接:方框与方框首尾相连。前一个方框的 输出,作为后一个方框的输入。 (2)并联连接:两个或多个方框,输入相同,输出为 各方框输出的代数和。 (3)反馈连接:一个方框的输出,输入到另一个方框, 得到的输出再返回作用于前一个方框的 输入端。如图2-37所示