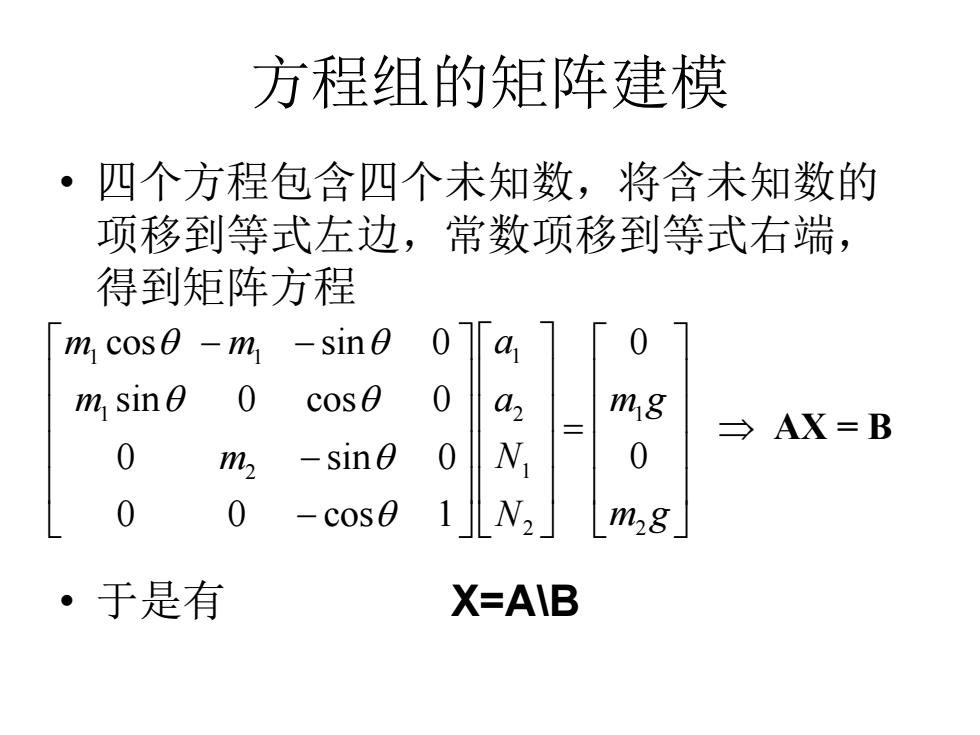
方程组的矩阵建模 ·四个方程包含四个未知数,将含未知数的 项移到等式左边,常数项移到等式右端, 得到矩阵方程 m cos-m -sin0 m sinO 0 cos0 0 a m18 →AX=B 0 m -sin0 0 N 0 0 0 -cos0 1]N2 mg ·于是有 X=AIB
方程组的矩阵建模 • 四个方程包含四个未知数,将含未知数的 项移到等式左边,常数项移到等式右端, 得到矩阵方程 • 于是有 X=A\B 1 1 1 1 2 1 2 1 2 2 cos sin 0 0 sin 0 cos 0 0 sin 0 0 0 0 cos 1 m m a m a m g m N N m g AX = B

程序exn623 m1=input(m1=【千克】): m2=input('m2=【千克】); theta=input('theta【度】=); theta=theta*pi/180;g=9.81; A=m1*cos(theta),-m1,-sin(theta),0;... m1*sin(theta),0,cos(theta),0;... 0 m2,-sin(theta),0;... 0 0,-cos(theta),1 ] B=[0,m1*g,0,m2*g]';X=A1B; a1=X(1),a2=X(2),N1=X(3),N2=X(4)
程序exn623 m1=input('m1=【千克】 '); m2=input('m2=【千克】 '); theta=input('theta【度】= '); theta=theta*pi/180; g=9.81; A = [ m1*cos(theta),-m1, -sin(theta), 0;... m1*sin(theta), 0, cos(theta), 0;... 0 , m2, -sin(theta), 0;... 0 , 0, -cos(theta), 1 ]; B = [ 0, m1*g, 0, m2*g]'; X=A\B; a1=X(1),a2=X(2),N1=X(3),N2=X(4)

运行结果 ·输入m1=2【kg】,m2=4【kg】,及theta=30 【deg】,得到 ·a1=6.5400【m/s2】;a2=1.8879【m/s2】 ·N1=15.1035【N】;N2=52.3200【N】 ·静力学平衡和动力学中求力与加速度关系的问题, 通常都可归结为线性方程组的求解,只要方程组列 写正确,用MATLAB的矩阵除法就可以方便而准确 的求出其解
运行结果 • 输入m1=2【kg】,m2=4【kg】,及theta=30 【deg】,得到 • a1 = 6.5400【m/s2】; a2 = 1.8879【m/s2】 • N1 = 15.1035【N】; N2 = 52.3200【N】 • 静力学平衡和动力学中求力与加速度关系的问题, 通常都可归结为线性方程组的求解,只要方程组列 写正确,用MATLAB的矩阵除法就可以方便而准确 的求出其解

例6-2-4碰撞问题 质量为m的小球以速度uO正面撞击质量为M的静止小球,假设 碰撞是完全弹性的,即没有能量损失,求碰撞后两球的速 度,及它们与两球质量比K=M/m的关系 解:◆建模设碰撞后两球速度都与uo同向,球的速度为u,球 M的速度为,列出动量守恒和能量守恒方程,则引入质量 比K=MWm和相对速度ur=u/uo,vr=vuo后,有 动量守恒 muo=mu+Mv 动能守恒 1 221 、n6=5n42+。2 2 化为 Ky,+u,=1 Ky,2+u,2=1
例6-2-4 碰撞问题 质量为m的小球以速度u0正面撞击质量为M的静止小球,假设 碰撞是完全弹性的,即没有能量损失,求碰撞后两球的速 度,及它们与两球质量比K=M/m的关系. 解: ◆建模 设碰撞后两球速度都与u0同向,球m的速度为u, 球 M的速度为v,列出动量守恒和能量守恒方程,则引入质量 比K=M/m和相对速度ur= u/u0 ,vr=v/u0后, 有 • 动量守恒 mu0=mu+Mv • 动能守恒 • 化为 2 2 2 0 1 1 1 2 2 2 mu mu Mv 2 2 1 1 r r r r Kv u Kv u

碰撞问题的方程 ·由(3) y,=(1-w,)/K (5) ·代入(4)》 (1-4,)+Kw,2=K (6) ·主动球的能量损失为 E。=2mG-)=gG0-42) ·展开并整理多项式(⑥),得 *0+小-0 ·可用roots命令求根
碰撞问题的方程 • 由(3) (5) • 代入(4) (6) • 主动球的能量损失为 • 展开并整理多项式(6),得 • 可用roots命令求根, 1 / r r v u K 2 1 r r u Ku K 2 2 2 2 0 0 1 ( ) (1 ) 2 2 m r m E m u u u u 1 2 2 1 1 1 0 r r u u K K K