例6-2-1运行结果 ·在检查曲线正确后,键入hold命令,把曲线保留下来,以便 用同样的初速,不同的射角,比较其曲线和最大射程。 。 ◆运行结果 ·输入初始速度(ms):50,输入初速方向(度):40 ·输入目标高度(米):8 ·得xf=237.4738 ·而初速方向为50度时, 80 。Xf=241.0454 60 .高低角0度 ·所得曲线见图6-2-1. 40 高纸角40度 20 目标高8米 0 50 100 150 200 250
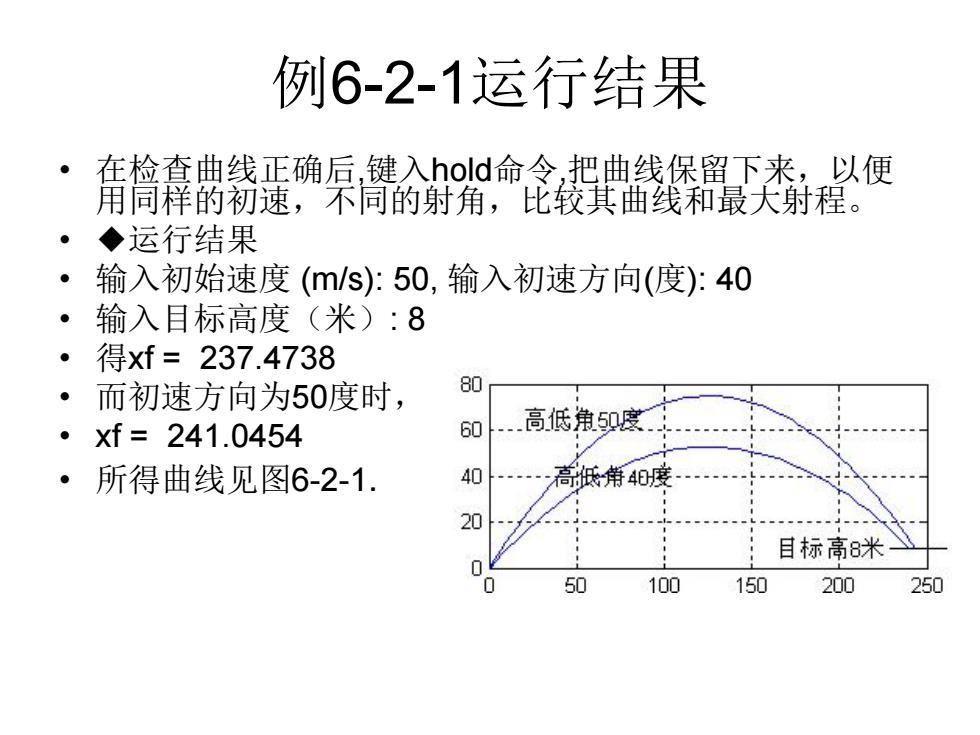
例6-2-1运行结果 • 在检查曲线正确后,键入hold命令,把曲线保留下来,以便 用同样的初速,不同的射角,比较其曲线和最大射程。 • ◆运行结果 • 输入初始速度 (m/s): 50, 输入初速方向(度): 40 • 输入目标高度(米): 8 • 得xf = 237.4738 • 而初速方向为50度时, • xf = 241.0454 • 所得曲线见图6-2-1

例6-2-2 质点的平面运动 给定质点沿x和y两方向的运动规律(代)和y(),求其运动轨迹, 并计算其对原点的角动量。 解: 建模:由用户输入解析表示式需要用到字符串的输入语句,其 第二变元为's,而运行这个字符串要用evai命令当x) 和y()都是周期运动时,所得的曲线就是李萨如图形. 动量矩等于动量与向径的叉乘(cross product):求速度需要用 导数,可用MATLAB的diff函数作近似导数计算。设角动 量为工,质点的动量为P,向径为下,则 工=rxP=rxmN 在x-y平面上的投影为 L=x·mvv-y:mvx
例6-2-2 质点的平面运动 给定质点沿x和y两方向的运动规律 x(t) 和 y(t),求其运动轨迹, 并计算其对原点的角动量。 解: 建模:由用户输入解析表示式需要用到字符串的输入语句,其 第二变元为’s’ ,而运行这个字符串要用eval命令.当x(t) 和 y(t)都是周期运动时,所得的曲线就是李萨如图形. 动量矩等于动量与向径的叉乘(cross product).求速度需要用 导数,可用MATLAB的diff函数作近似导数计算。设角动 量为 ,质点的动量为 ,向径为 ,则 在x-y平面上的投影为 L L r P = r mv P r L y x x mv y mv

程序exn622 ×=input((':,'s);y=input((':,'s');%读入字符串 tf input('tf=') Ns=100;t=linspace(0,tf,Ns);dt=tf/(Ns-1); %分Ns个点,求出时间增量dt xPlot=eval(x);yPlot=eval(y); %计算各点x(),y)的近似导数和角动量。 p_x=diff(xPlot)/dt;p_x M dx/dt p_y diff(yPlot)/dt;p_y M dy/dt %求角动量 LPlot xPlot(1:Ns-1).*p_y yPlot(1:Ns-1).*p_x; %画出轨迹及角动量随时间变化的曲线
程序exn622 x = input(': ' , 's'); y = input(': ' , 's'); % 读入字符串 tf = input(' tf= '); Ns=100; t=linspace(0,tf,Ns); dt=tf/(Ns-1); % 分Ns个点,求出时间增量dt xPlot=eval(x);yPlot=eval(y); % 计算各点x(t), y(t)的近似导数和角动量。 p_x = diff(xPlot)/dt; % p_x = M dx/dt p_y = diff(yPlot)/dt; % p_y = M dy/dt %求角动量 LPlot = xPlot(1:Ns-1).* p_y - yPlot(1:Ns-1).* p_x; % 画出轨迹及角动量随时间变化的曲线

程序运行结果 运行此程序,输 20 400 ·x=t.*cos(t) 300 ·y=t.*sin(t) ·tf=20 0 200 ·后,得出图6-2 100 ·如果输入 20 0 X=C0s(2*t) 0 0 10 20 ·y=sin(3*t) 图6-2按方程x=tcos(),y=tsin()画出 轨迹及角动量曲线
程序运行结果 运行此程序,输入 • x=t.*cos(t) • y=t.*sin(t) • tf=20 • 后,得出图6-2-2。 • 如果输入 • x=cos(2*t) • y=sin(3*t) 0 -20 0 20 x y 0 10 20 0 100 200 300 400 图6-2 按方程x=tcos(t),y=tsin(t)画出 轨迹及角动量曲线
例6-2-3质点系的动力学 物体A(质量为m1)在具有斜面的物体B(质量为m2)上靠重力 下滑,设斜面和地面均物摩擦力,求A沿斜面下滑的相对 加速度a1和B的加速度a2,并求斜面和地面的支撑力N1 及N2. 解:建模,对物体A,列出方程 m (a cose-a2)=N sine (1) B ma sin =mg-N coso (2) 对物体B,列出方程 ma,N sinO (3) N,-N cose-m2g=0 (4)
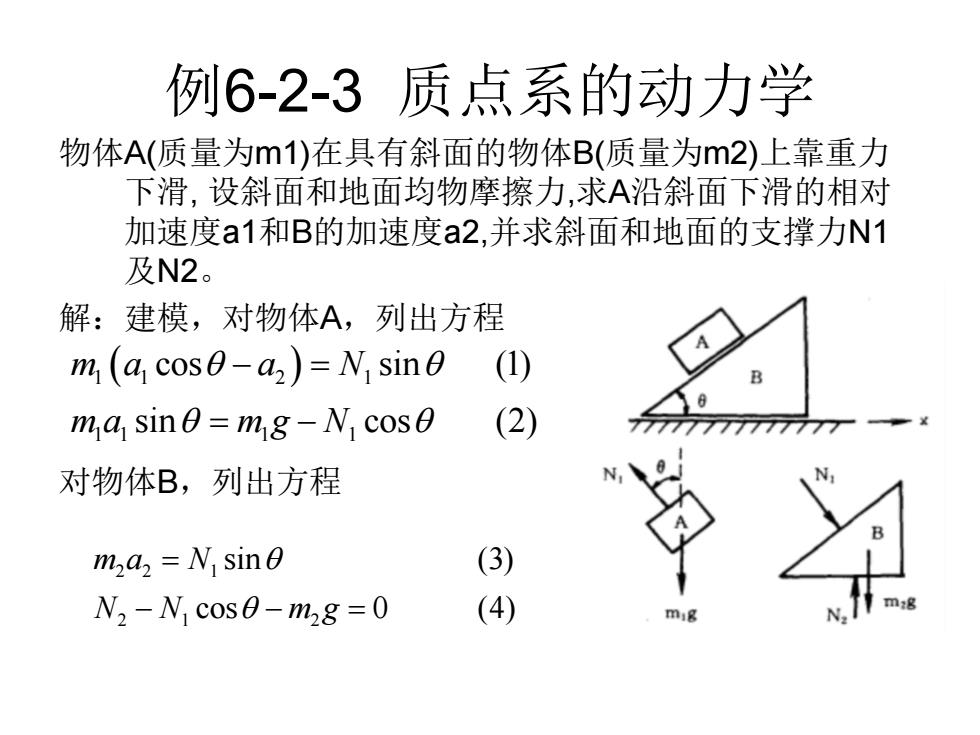
例6-2-3 质点系的动力学 物体A(质量为m1)在具有斜面的物体B(质量为m2)上靠重力 下滑, 设斜面和地面均物摩擦力,求A沿斜面下滑的相对 加速度a1和B的加速度a2,并求斜面和地面的支撑力N1 及N2。 解:建模,对物体A,列出方程 对物体B,列出方程 1 1 2 1 1 1 1 1 cos sin (1) sin cos (2) m a a N m a m g N 2 2 1 2 1 2 sin (3) cos 0 (4) m a N N N m g