
变换矩阵行列式的意义 ·对二维空间(平面),行列式的几何意义是两个基向量所 构成的平行四边形的面积。一个变换的行列式作用于某图 形所造成的新图形的面积变化倍数,等于该变换的行列式。 可以看出,A1,A4和A5的行列式绝对值都是 所以变换 后图形的面积不会发生改变。而A2和A3的行列式分别为 1.5和0.5,变换后图形面积的增加和减小倍数恰好于这两 个值相对应。各特征值和特征向量对图形的影响将在下节 讨论。 连续的线性变换可以表为变换矩阵的连乘。,比如先后进行 两次转动, 每次转角分别为α和邛,则两次线性变换矩阵的 连乘积为: cosa-sna‖ )-sin(a+B) A An- )cos(a+B) 。 其结果与转动的变换相同
变换矩阵行列式的意义 • 对二维空间(平面),行列式的几何意义是两个基向量所 构成的平行四边形的面积。一个变换的行列式作用于某图 形所造成的新图形的面积变化倍数,等于该变换的行列式。 可以看出,A1,A4和A5的行列式绝对值都是一,所以变换 后图形的面积不会发生改变。而A2和A3的行列式分别为 1.5和0.5,变换后图形面积的增加和减小倍数恰好于这两 个值相对应。各特征值和特征向量对图形的影响将在下节 讨论。 • 连续的线性变换可以表为变换矩阵的连乘。比如先后进行 两次转动,每次转角分别为α和β,则两次线性变换矩阵的 连乘积为: • 其结果与转动的变换相同。 ( ) ( ) ( ) ( ) cos -sin cos -sin cos -sin , sin cos sin cos sin cos + + = = + + A A

线性变换表述物体的形变 二维矩阵的特征值表示该变换在原图形的特征向量的方向上 的放大量。,例如矩阵A1的特征向量阵p1的第一列10] (代表癀轴)对应于其第一个特征值入1(1,1)=-1,p1的第 列[01T(代表纵轴)对应于其第二个特征值入(2,2)=1, 它表示横轴方向的增益为-1,纵轴方向的增益为,其结 果是把原图中横轴正方向的部分变换到新图的负方向去了, 而纵缅方向的尺度不变;A2的特征向量阵p2第一列[01]立 (代表纵轴)对应的特征值为入2(1,1)=1,其第二列10j订 (代表横轴)对应的特征值为λ22,2)=1.5,即纵轴方向 的增益为1,因而使新图和原图在纵轴方向尺度不变,横 轴方向的尺度增益为1.5。 再看A3,其第一特征向量[01]T对应的特征值为0.5;第 二特征向量[10]对应的特征值为1,说明新图形纵向是原 图形的0.5倍,横向和原图形的相同,图中反映的也确实 是这种情况
线性变换表述物体的形变 二维矩阵的特征值表示该变换在原图形的特征向量的方向上 的放大量。例如矩阵A1的特征向量阵p1的第一列[1 0]T (代表横轴)对应于其第一个特征值λ1 (1,1)= -1,p1的第 二列[0 1]T(代表纵轴)对应于其第二个特征值λ1 (2,2)= 1, 它表示横轴方向的增益为-1,纵轴方向的增益为1,其结 果是把原图中横轴正方向的部分变换到新图的负方向去了, 而纵轴方向的尺度不变;A2的特征向量阵p2第一列[0 1]T (代表纵轴)对应的特征值为λ2(1,1)= 1,其第二列[1 0]T (代表横轴)对应的特征值为λ2(2,2)= 1.5,即纵轴方向 的增益为1,因而使新图和原图在纵轴方向尺度不变,横 轴方向的尺度增益为1.5。 • 再看A3,其第一特征向量[0 1]T对应的特征值为0.5;第 二特征向量[1 0]T对应的特征值为1,说明新图形纵向是原 图形的0.5倍,横向和原图形的相同,图中反映的也确实 是这种情况
正体字母变换为斜体字母 00.500.506.06.005.505.50 0 例5.2数据矩阵 06.4208.008.001.58 8 为英文大写N图形的各个节点, 求: (1)用plot语句在子图1中画出其 形状; (2)取A=[1,0.25;0,1]作为变换矩 阵对x进行变换,并画出y=Ax 5 10 10 的图形; 图5-4例5.2生成的N字符图形 (③)对结果进行讨论
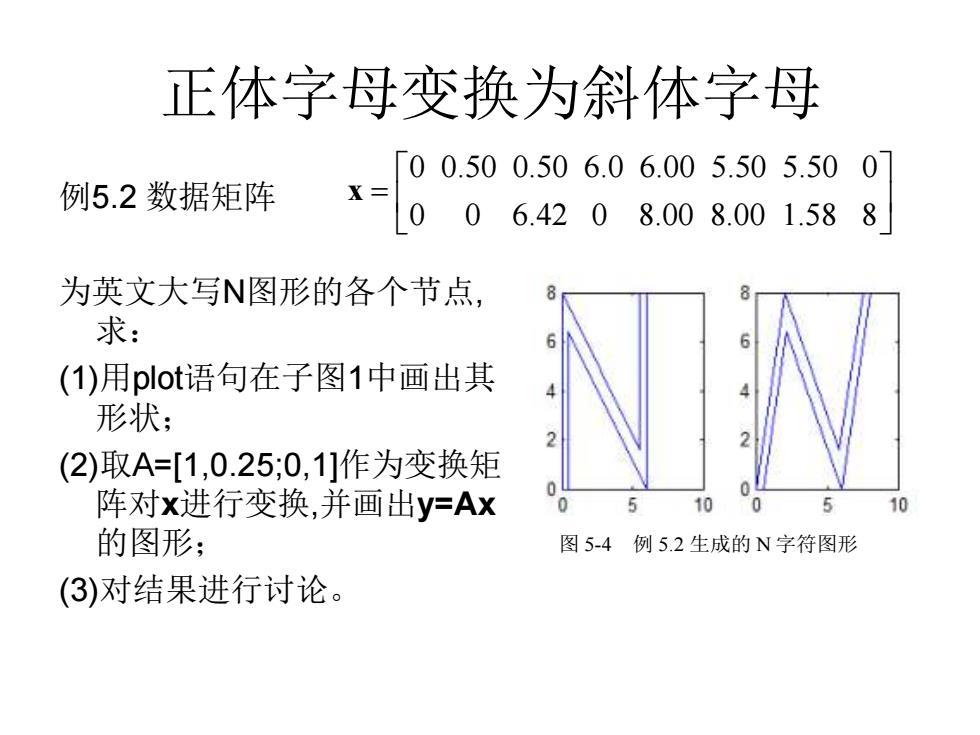
正体字母变换为斜体字母 例5.2 数据矩阵 为英文大写N图形的各个节点, 求: (1)用plot语句在子图1中画出其 形状; (2)取A=[1,0.25;0,1]作为变换矩 阵对x进行变换,并画出y=Ax 的图形; (3)对结果进行讨论。 0 0.50 0.50 6.0 6.00 5.50 5.50 0 0 0 6.42 0 8.00 8.00 1.58 8 = x .5.1 图 5-4 例 5.2 生成的 N 字符图形

程序pla502及其运行结果 ·x0=[0,0.5,0.5,6,6,5.5,5.5,0;0,0,6.42,0,8,8,1.58,8]; ·=[0,0(:,1)小;%把首顶点坐标补到末顶点之后 ·A=[1,0.25;0,1];y=A*X; ·subplot(1,2,1),plot(x(1,),x(2,:)》 。subplot(1,2,2),plot(y1,),y(2,)》 。 生成的图形见图5-4,这个例子说明在设计计算机 字库时,斜体字库可以不必单独建立,只要对正 体字库进行适当的线性变换,就可以实现斜体字, 用这个方法可以节约大量的人力,并可节约存储 量
程序pla502及其运行结果 • x0=[0,0.5,0.5,6,6,5.5,5.5,0;0,0,6.42,0,8,8,1.58,8]; • x=[x0,x0(:,1)]; % 把首顶点坐标补到末顶点之后 • A=[1,0.25;0,1]; y=A*x; • subplot(1,2,1),plot(x(1,:),x(2,:)) • subplot(1,2,2),plot(y(1,:),y(2,:)) • 生成的图形见图5-4,这个例子说明在设计计算机 字库时,斜体字库可以不必单独建立,只要对正 体字库进行适当的线性变换,就可以实现斜体字, 用这个方法可以节约大量的人力,并可节约存储 量

5.2.2非同维线性变换的用途 。 这里所实现的还只是同维空间(平面一平面)之间的变 换,实际上还有不同维空间之间的变换。比如用1×2的变 换矩阵左乘数据矩阵x,将得到y=Ax[0,1,1,0]。此时原二 维向量x被变换为一维的新向量y。它的实质是把原方格图 形投影到横坐标轴上。四个顶点变换(投影)为横坐标上 的两个点0和1。 把三维的物体图投影到两维平面具有更广泛的用途,最直 接的就是三维动漫技术。 三维到二维投影的另一个最新用途则是3D打印技术,它 把由计算机辅助设计(CAD)生成的立体模型图纸,细密地 分层截取它的截面形状,一层一层地打印粘叠起来,恢复 复杂的三维原型。这就需要2×3维的变换矩阵
5.2.2 非同维线性变换的用途 • 这里所实现的还只是同维空间(平面——平面)之间的变 换,实际上还有不同维空间之间的变换。比如用1×2的变 换矩阵左乘数据矩阵x,将得到y=Ax=[0,1,1,0]。此时原二 维向量x被变换为一维的新向量y。它的实质是把原方格图 形投影到横坐标轴上。四个顶点变换(投影)为横坐标上 的两个点0和1。 • 把三维的物体图投影到两维平面具有更广泛的用途,最直 接的就是三维动漫技术。 • 三维到二维投影的另一个最新用途则是3D打印技术,它 把由计算机辅助设计(CAD)生成的立体模型图纸,细密地 分层截取它的截面形状,一层一层地打印粘叠起来,恢复 复杂的三维原型。这就需要2×3维的变换矩阵