西安电子科技大学：《实用大众线性代数》课程PPT教学课件（MATLAB版）第5章 线性变换及其特征

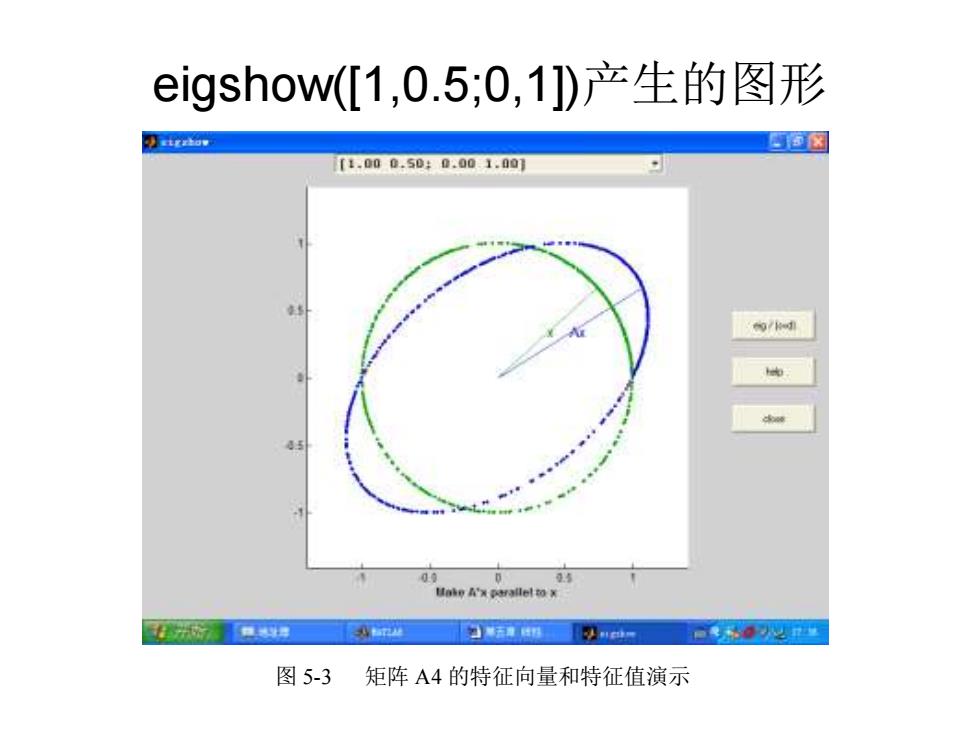
变换矩阵A的意义 把这些变换矩阵看做两个二维列向量的组合A=[α1，a2], Q1,α2也被称作此变换的基向量，图上画出了这些向量。 线性变换A对x平面上不同方向的向量产生的作用是不同的。 可以取x平面上的一个单位向量，让它渐渐转动，看看变 换后的y=Ax如何变化。MATLAB设计了这样一个演示程 序，程序名为eigshow,其输入变元是二维矩阵A。键入 eigshow([1,0.5;0,1)就出现了所示的图形。 用鼠标左键点住绿色的x向量并拖动它围绕原点转动，它表 示原坐标系中的单位向量。图中同时出现以蓝色表示的 Ax向量，它表示变换后的新向量y。y与x在长度和相角上 的不同就表示了该变换造成的这个向量的幅度增益和相角 增量

变换矩阵A的意义 把这些变换矩阵看做两个二维列向量的组合A=[α1 ,α2 ]， α1 ,α2也被称作此变换的基向量，图上画出了这些向量。 线性变换A对x平面上不同方向的向量产生的作用是不同的。 可以取x平面上的一个单位向量，让它渐渐转动，看看变 换后的y=Ax如何变化。MATLAB设计了这样一个演示程 序，程序名为eigshow，其输入变元是二维矩阵A。键入 eigshow([1,0.5;0,1])就出现了所示的图形。 用鼠标左键点住绿色的x向量并拖动它围绕原点转动，它表 示原坐标系中的单位向量。图中同时出现以蓝色表示的 Ax向量，它表示变换后的新向量y。y与x在长度和相角上 的不同就表示了该变换造成的这个向量的幅度增益和相角 增量

eigshow([1,0.5;0,1])产生的图形 [1.000.50#0.001.007 9/01 ake A'x porallel to 可 习东a韩【加eR0 图5-3 矩阵A4的特征向量和特征值演示

eigshow([1,0.5;0,1])产生的图形 图 5-3 矩阵 A 4 的特征向量和特征值演示

图上的特征值和特征向量 当两个向量处在同一条直线上时（包括同向和反向），表示 两者之间的方向重合，只差一个实数乘子入。 AX=λX (5.1.7) 把这时的向量x称为特征向量，对应的乘子λ称为特征值。 在这个图中，当x转到士1的水平位置时，Ax也恰好与x重合， 并具有同样的长度，说明其特征值等于1，特征向量则是 实数单位向量1+j0。至于不同方向的x所产生的y=Ax,只 靠特征值和特征向量就无法解释了，必须观察整个x-Ax的 曲线。例如在x位于45度附近时，Ax变得很长，这就说明 了原来单位方格的对角线被拉长，形成了剪切现象

图上的特征值和特征向量 当两个向量处在同一条直线上时（包括同向和反向），表示 两者之间的方向重合，只差一个实数乘子λ。 Ax=λx （5.1.7） 把这时的向量x称为特征向量，对应的乘子λ称为特征值。 在这个图中，当x转到±1的水平位置时，Ax也恰好与x重合， 并具有同样的长度，说明其特征值等于1，特征向量则是 实数单位向量1+j0。至于不同方向的x所产生的y=Ax，只 靠特征值和特征向量就无法解释了，必须观察整个x-Ax的 曲线。例如在x位于45度附近时，Ax变得很长，这就说明 了原来单位方格的对角线被拉长，形成了剪切现象

特征值和特征向量的意义 ·矩阵A的特征向量和特征值是指能满足特征 方程(5.1.7)的x和入，两者分别表徵了特征点 所处的方向和畸变的大小。为了进一步看 出矩阵的特征和它们变换的效果之间的关 系，可计算出这五个矩阵的行列式和特征值。 特征向量p和特征值λ的手工计算很繁，只 要求读者能用MATLAB计算。调用的命令 是[p,lambda]=eig(A),这里同时计算了A的 行列式及特征值，结果如下：

特征值和特征向量的意义 • 矩阵A的特征向量和特征值是指能满足特征 方程(5.1.7)的x和λ，两者分别表徵了特征点 所处的方向和畸变的大小。为了进一步看 出矩阵的特征和它们变换的效果之间的关 系,可计算出这五个矩阵的行列式和特征值。 特征向量p和特征值λ的手工计算很繁，只 要求读者能用MATLAB计算。调用的命令 是[p,lambda]=eig(A)，这里同时计算了A的 行列式及特征值，结果如下:

五种变换矩阵的特征值特征向量 n=daa=-ln-[09=[)9 (5.1.8) de)-15 (5.1.9) n=d=5-[8 (5.1.10) 0 1a[8 m-w=-L-[094[0] (5.1.11) 0 )0.866-0.5i (5.1.12)

五种变换矩阵的特征值特征向量 1 1 1 0 1 0 det( ) 1, , 0 1 0 1 D      − = = − = =         A p 1 1 2 2 0 1 1.0 0 det( ) 1.5, 1 0 0 1.5 D      = = = =         A p 2 2 ， 3 3 0 1 0.5 0 det( ) 0.5, , 1 0 0 1.0 D      = = = =         A p 3 3 4 4 1.0 -1.0 1 0 det( ) 1, , 0. 0. 0 1 D      = = = =         A p 4 4 5 5 0.7071 0.7071 0.866 + 0.5i 0 1, , - 0.7071i 0.7071i 0 0.866 - 0.5i D      = = =         p5 (5.1.8) (5.1.9) (5.1.10) (5.1.11) (5.1.12)