
把二维变换为三维向量的用途 ·反过来,把二维向量变换为三维向量,即 把平面上的向量换成为空间向量,在某些 情况下是很有用的。比如刚体在平面上的 运动要用两个平移和一个转动来描述,转 动可以从上面的线性变换A5得到,但平移 却不是一个线性变换。要完全用矩阵乘法 来描述刚体的运动,就要刚体位置的描述 增加一维,采用下节介绍的“齐次坐标 系
把二维变换为三维向量的用途 • 反过来,把二维向量变换为三维向量,即 把平面上的向量换成为空间向量,在某些 情况下是很有用的。比如刚体在平面上的 运动要用两个平移和一个转动来描述,转 动可以从上面的线性变换A5得到,但平移 却不是一个线性变换。要完全用矩阵乘法 来描述刚体的运动,就要刚体位置的描述 增加一维,采用下节介绍的“齐次坐标 系

5.2.3用线性变换描述刚体的运动 前面所研究的矩阵和向量的算法,都是在向量空间内有效 的。所谓向量空间V,要求其所属的向量对加法和数乘满 足封闭性:即:①若a,beV,则a+beV,②若aeV,则ka V,其中k为任意实数。但刚体的平移不满足这个条件。 ·因为:①、设ya=a+c;yb=b+c;则它们的和为 y=ya+yb=a+xb+2cx+c,可见它对加法不封闭; ·②、设ya=a+c;将它乘以常数k,有 y=kya=k(Xa+c)=kXa+kcxa+c-x+c,可见它对乘法也不 封闭;就是说,平移不符合线性变换的规则,无法用矩阵 乘法来实现平移变换y=x+c。 ·如把平面问题映射到三维空间来建立方程,这就可能把x 和y由扩展了的向量空间来涵盖
5.2.3 用线性变换描述刚体的运动 • 前面所研究的矩阵和向量的算法,都是在向量空间内有效 的。所谓向量空间V,要求其所属的向量对加法和数乘满 足封闭性:即:①若a,bV,则a+b V, ②若a V ,则ka V,其中k为任意实数。但刚体的平移不满足这个条件。 • 因为:①、设 ya=xa+c;yb=xb+c;则它们的和为 y=ya+yb=xa+xb+2c≠x+c,可见它对加法不封闭; • ②、设 ya=xa+c;将它乘以常数k,有 y=kya=k(xa+c)=kxa+kc≠kxa+c=x+c,可见它对乘法也不 封闭;就是说,平移不符合线性变换的规则,无法用矩阵 乘法来实现平移变换y=x+c。 • 如把平面问题映射到三维空间来建立方程,这就可能把x 和y由扩展了的向量空间来涵盖

齐次坐标系中的平移矩阵 ·把原来通过原点的平面沿垂直方向提高一个单位,与原平 面保持平行,把原来的二维的x用三维向量来表示。这样 的坐标系称为齐次坐标系(Homogeneous coordinate)。 可以把向量x和平移矩阵M写成: 1 0 X三 X2 M= 0 C2 1 0 1 ·于是有 X1+C1 y= y2 =M·X= x2+c2 1 1 可见三维齐次坐标中的前两个分量实现了平移运算的要求
齐次坐标系中的平移矩阵 • 把原来通过原点的平面沿垂直方向提高一个单位,与原平 面保持平行,把原来的二维的x用三维向量来表示。这样 的坐标系称为齐次坐标系(Homogeneous coordinate )。 可以把向量x和平移矩阵M写成: • 于是有 可见三维齐次坐标中的前两个分量实现了平移运算的要求。 1 2 1 x x = x 1 2 1 0 0 1 0 0 1 c c = M 1 1 1 2 2 2 x +c x +c 1 1 y y = = y = M x

齐次坐标系中的旋转矩阵 ·对象若同时有旋转和平移,可以分别列出旋转矩阵和平移 矩阵。不过此时的旋转矩阵也要改为3×3维,这可以把上 述A5中增加第三行和第三列,置A(3,3)=1,其余新增元素 为零。 cost -sint 0 A5= sin t cos t 0 0 1 把平移矩阵M左乘旋转矩阵A5就得到既包括平移,又包括 转动的平面齐次坐标系的变换矩阵。 cos t -sint c A=M*A5= sin t cos t 0 0 要注意变换矩阵的相乘次序是不符合交换律的
齐次坐标系中的旋转矩阵 • 对象若同时有旋转和平移,可以分别列出旋转矩阵和平移 矩阵。不过此时的旋转矩阵也要改为3×3维,这可以把上 述A5中增加第三行和第三列,置A(3,3)=1,其余新增元素 为零。 • 把平移矩阵M左乘旋转矩阵A5就得到既包括平移,又包括 转动的平面齐次坐标系的变换矩阵。 • 要注意变换矩阵的相乘次序是不符合交换律的。 cos t -sin t 0 sin t cos t 0 , 0 0 1 = A5 1 2 cos t -sin t c sin t cos t c , 0 0 1 = = A M * A5
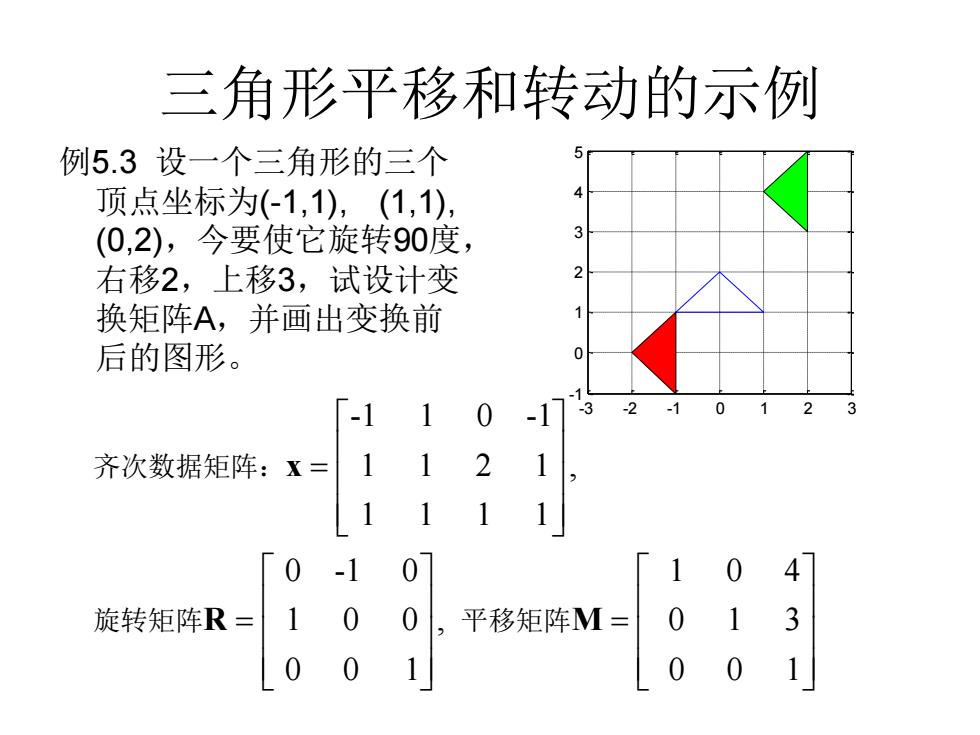
三角形平移和转动的示例 例5.3设一个三角形的三个 顶点坐标为(-1,1),(1,1), (0,2),今要使它旋转90度, 右移2,上移3,试设计变 换矩阵A,并画出变换前 后的图形。 ( -1 2 齐次数据矩阵:X= 1 2 1 0 -1 0 104 旋转矩阵R= 1 0 0 平移矩阵M= 0 0 0 0 0
三角形平移和转动的示例 例5.3 设一个三角形的三个 顶点坐标为(-1,1), (1,1), (0,2),今要使它旋转90度, 右移2,上移3,试设计变 换矩阵A,并画出变换前 后的图形。 -3 -2 -1 0 1 2 3 -1 0 1 2 3 4 5 -1 1 0 -1 1 1 2 1 , 1 1 1 1 0 -1 0 1 0 4 1 0 0 , 0 1 3 0 0 1 0 0 1 = = = x R M 齐次数据矩阵: 旋转矩阵 平移矩阵