
证明思略: 1)若D既是X-型区域,又是Y-型区域,且 【装ay-f.0x -儿8ad-fPr心x,n: ② ① ②两式相加得 心,是-影d-f+0y 2)若D不满足以上条件, 分割区域D为有限个上述形式的区域 HIGH EDUCATION PRESS O◆008 定理1目录上页下页返回结束
证明思路: ① ② ①、②两式相加得: ( ) = + − D L x y P x Q y y P x Q d d d d 定理1 目录 上页 下页 返回 结束 1) 若D 既是 X - 型区域 , 又是 Y - 型区域 , 且 2) 若D不满足以上条件, 分割区域 D 为有限个上述形式的区域

证明:1)若D既是X-型区域,又是Y-型区域,且 D: p1(x)≤y≤02(x) a≤x≤b 4y)≤x≤Ψ2(y) x=(y S人 c≤y≤d 则器adw=-ar h x -[Q(w2().y)dy-["Q().)dy =∫cB0x,dy-「cc(xi =S(.y+∫Eac0(x,=④0xma HIGH EDUCATION PRESS 定理1目录上页下页返回结束
证明: 1) 若D 既是 X - 型区域 , 又是 Y - 型区域 , 且 a x b x y x D ( ) ( ) : 1 2 则 x y x Q D d d = d c Q( ( y), y )dy 2 ( ) ( ) 2 1 d y y x x Q = CBE Q(x, y)dy + EAC Q(x, y)dy − d c Q( ( y), y )dy 1 = d c dy d c y o x E C A B a b D 定理1 目录 上页 下页 返回 结束 2 x y = ( )

即 是ad-fexa ① 同理可证 -dat-fPxarx ② ① ②两式相加得 )ydy HIGH EDUCATION PRESS 定理1目录上页下页返回结束
即 同理可证 ① ② ①、②两式相加得: ( ) = + − D L x y P x Q y y P x Q d d d d 定理1 目录 上页 下页 返回 结束
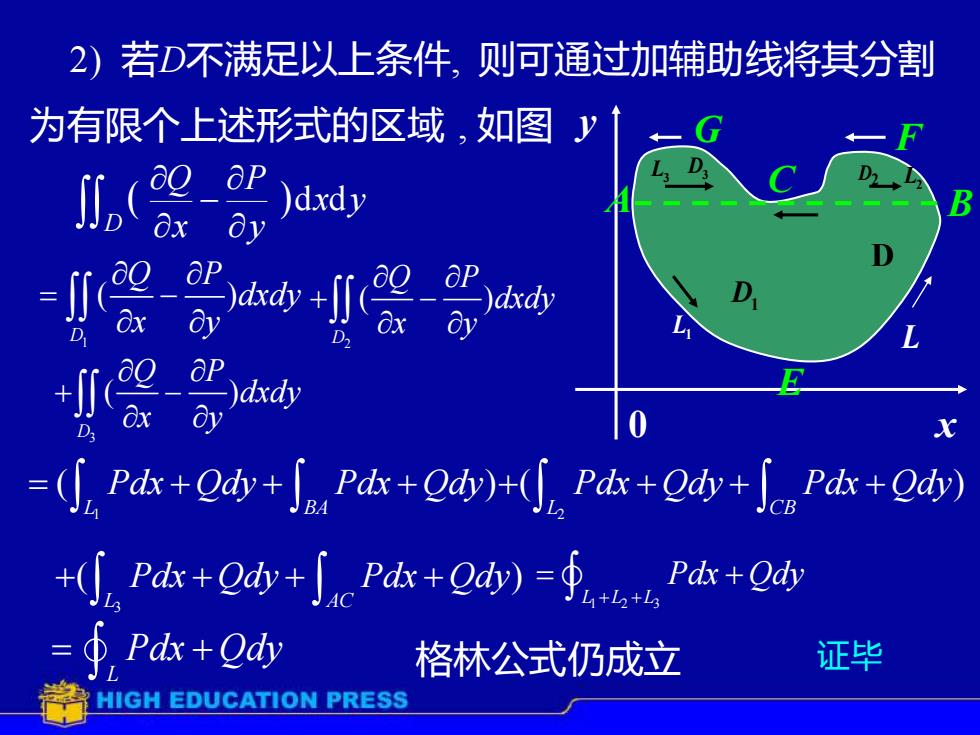
2)若D不满足以上条件,则可通过加辅助线将其分割 为有限个上述形式的区域,如图》 0 =Pdk+Qdy+Pd+d)Pds+Qdy+ScPdx+Ody) +Pk++∫Pk+d)=∮hPh+0w Pdx Qdy 格林公式仍成立 证毕 HIGH EDUCATION PRESS
1 L L L2 L3 D D1 D2 D3 x y 0 A B C E G F 1 ( ) D Q P dxdy x y = − 2 ( ) D Q P dxdy x y + − 3 ( ) D Q P dxdy x y + − L L L 1 2 3 Pdx Qdy + + = + Ñ L = + Pdx Qdy Ñ 格林公式仍成立 2) 若D不满足以上条件, 则可通过加辅助线将其分割 为有限个上述形式的区域 , 如图 ( ) x y y P x Q D d d − 1 ( ) L BA = + + + Pdx Qdy Pdx Qdy 2 ( ) L CB + + + + Pdx Qdy Pdx Qdy 3 ( ) L AC + + + + Pdx Qdy Pdx Qdy 证毕

xdy-fPdx+Ody 几点说明 >若D为复连通区域: 则曲线应包括内外所有边界 L=L1+L2+L3并且取正向 >格林公式的实质: 建立了平面上的曲线积分与二重积分的联系, 是牛顿莱布尼茨公式在平面上的推广。 >主要用途:实现曲线积分与二重积分之间的转换 (1)利用格林公式求曲线或二重积分 (2)利用曲线积分计算平面区域的面积 HIGH EDUCATION PRESS
L3 L2 几点说明: ➢若D为复连通区域: 则曲线 L1 L 应包括内外所有边界 L = L1 + L2 + L3 并且取正向. ➢格林公式的实质: ➢主要用途:实现曲线积分与二重积分之间的转换 D = + − D L x y P x Q y y P x Q d d d d 建立了平面上的曲线积分与二重积分的联系, 是牛顿莱布尼茨公式在平面上的推广。 (2)利用曲线积分计算平面区域的面积 (1)利用格林公式求曲线或二重积分