
引理一次邻换改变排列的奇偶性. 证不失一般性,设排列pP2…P,j9929:经一次邻换变为 P1P2…p,jiq192…93 ☒无法显示该图片。 卫P2…p,和q92…9,的各数字间的 相互位置以及它们分别与i或j的相互位置并无改变,因此它们的 逆序个数不变.由于i,j相互调换位置后,使排列 PP2…P,jiq92…9的逆序数比原来排列PP2…p,jq192…9 增1或减1,故排列P1P2…P,j992…9,与P1P2…Pjiq92…9的 奇偶性不同命题得证 7
7 1 2 1 2 s t p p p q q q 和 的各数字间的 相互位置以及它们分别与 或 的相互位置并无改变,因此它们的 逆序个数不变. i j 引理 一次邻换改变排列的奇偶性. 证 不失一般性,设排列 经一次邻换变为 1 2 1 2 , s t p p p jiq q q 1 2 1 2 s t p p p ijq q q 增1或减1, 故排列 与 的 奇偶性不同.命题得证 1 2 1 2 s t p p p ijq q q i j , 1 2 1 2 s t p p p jiq q q 由于 相互调换位置后,使排列 的逆序数比原来排列 1 2 1 2 s t p p p ijq q q 1 2 1 2 s t p p p jiq q q

定理1一次对换必改变排列的奇偶性. 证设排列 p1…pig…fmj91…9% (1)》 经一次对换化为排列 卫1…PJr…Tm1q19 (2) 根据引理,只要证明由(1)到(2)的一次对换可以经过奇 数次邻换来实现就可以了. 事实上,在排列(1)中将数字i依次向右做m+1次邻换, 得排列 p1…ph1mjiq1…9 再将上述排列中的数字j依次向左做m次邻换,得到的排列 即为(2). 总之,(1)可经2m+1)次邻换化为(2).证毕. 8
8 根据引理,只要证明由(1)到(2)的一次对换可以经过奇 数次邻换来实现就可以了. 事实上,在排列(1)中将数字 依次向右做 次邻换, 得排列 i m +1 l m qk p1 p r1 r jiq1 再将上述排列中的数字 依次向左做 次邻换,得到的排列 即为(2). j m 总之,(1)可经( 2m +1 )次邻换化为(2).证毕. 定理1 一次对换必改变排列的奇偶性. 证 设排列 (1) 经一次对换化为排列 (2) l m qk p1 p ir1 r jq1 l m qk p1 p jr1 r iq1

例2已知3口452☐为一个六级排列,将数字1和6填入口内,使 其成为奇排列 解我们可以将数字1和6随意填入两个口内,然后求此排列的 逆序数.如果逆序数是奇数,该排列即为所求;如果逆序数为偶 数,由定理1,将数字1和6的位置对调,便得所求的排列. 今将数字1填入第一个口内,将数字6填入第二个口内,得排列 314526,则该排列的逆序数为 x(314526)=0+1+0+0+3+0=4, 即排列314526为偶排列,由定理1,将数字1和6的位置对调,得 奇排列364521. 最后我们指出,本节讨论的前个自然数的排列问题可以推广 到任意n个不同元素的全排列中去, 9
9 由定理1,将数字1和6的位置对调,得 奇排列364521. 例2 已知3□452□为一个六级排列,将数字1和6填入□内,使 其成为奇排列. 解我们可以将数字1和6随意填入两个□内,然后求此排列的 逆序数.如果逆序数是奇数,该排列即为所求;如果逆序数为偶 数,由定理1,将数字1和6的位置对调,便得所求的排列. 今将数字1填入第一个□内,将数字6填入第二个□内,得排列 314526,则该排列的逆序数为 (314526) 0 1 0 0 3 0 4, = + + + + + = 即排列314526为偶排列, 最后我们指出, 本节讨论的前 n 个自然数的排列问题可以推广 到任意 n 个不同元素的全排列中去
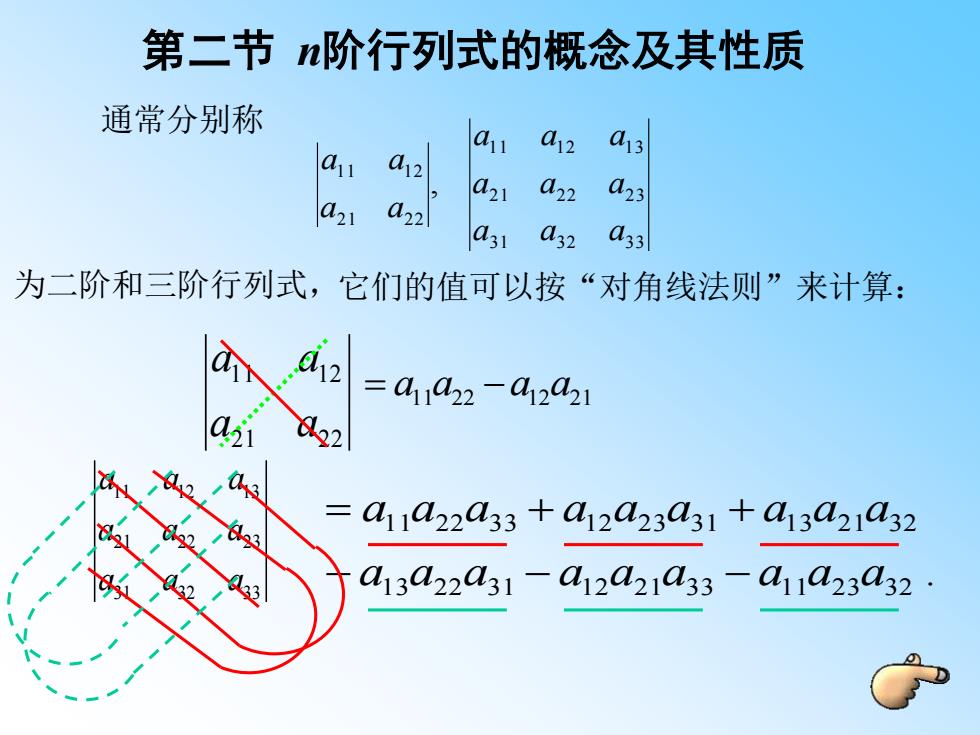
第二节n阶行列式的概念及其性质 通常分别称 412a413 a21 a22 a23 a21 22 a31 43233 为二阶和三阶行列式,它们的值可以按“对角线法则”来计算: =411422-412421 2 = 411022a33+a12a23a31+413Q21032 013022031-a12021a33-a11023032 ①
11 11 12 13 21 22 23 31 32 33 a a a a a a a a a 第二节 n阶行列式的概念及其性质 它们的值可以按“对角线法则”来计算: 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 2 1 2 2 1 1 1 2 , a a a a a a a a a a a a a 为二阶和三阶行列式, 通常分别称 . 1 3 2 2 3 1 1 2 2 1 3 3 1 1 2 3 3 2 1 1 2 2 3 3 1 2 2 3 3 1 1 3 2 1 3 2 a a a a a a a a a a a a a a a a a a − − − = + + 21 22 11 12 a a a a = a11a22 −a12a21

定义3将n2个数 a(i,j=1,2,…,n) 排成如下形式 412 ain a21 2 (3) am an2 ar 称为一个阶行列式.“|”是行列式的记号.行列式中每个横排 称为一行,每个竖排称为一列,数a,称为该行列式的第行第j列 的元素,i和j分别称为元素a,的行标和列标. ★ 定义4n阶行列式(3)中取自不同行又不同列的n个元素的乘 积aaan称为该行列式的一个均匀分布乘积项,简称为均布项 排列i2…in称为它的行标排列,j2…j称为它的列标排列. 我们规定:一个均布项中诸元素互换位置得到的所有均布项都 视为同一个均布项, 12
12 定义3 将 n 2 个数 a i j n ij ( , 1,2, , ) = 排成如下形式 11 12 1 21 22 2 1 2 (3) n n n n nn a a a a a a a a a 积 称为该行列式的一个均匀分布乘积项,简称为均布项. 定义4 n 阶行列式(3)中取自不同行又不同列的 n 个元素的乘 n n ai j ai j ai j 1 1 2 2 排列 i 1 i 2 i n 称为它的行标排列, j 1 j 2 j n 称为它的列标排列. 我们规定:一个均布项中诸元素互换位置得到的所有均布项都 视为同一个均布项. 称为一个 阶行列式.“| |”是行列式的记号.行列式中每个横排 称为一行,每个竖排称为一列,数 称为该行列式的第 行第 列 的元素, 和 分别称为 元素 的行标和列标. n ij a i j i j aij