
导航 学以致用 1.设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底.给出下 列向量组:①{a,b,x};②{x,y,z;③{b,c,z;④{xy,a+b+c}. 其中可以作为空间的基底的向量组有 个 答案:3
导航 学以致用 1.设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底.给出下 列向量组:①{a,b,x};②{x,y,z};③{b,c,z};④{x,y,a+b+c}. 其中可以作为空间的基底的向量组有 个. 答案:3

导 解析:如图,设a=AB,b=A41,c=AD,则x=AB1,y=AD1,Z=AC a+b+c=AC.由A,B1,D1,C四,点不共面可知,向量X,y,z不共面, 故{x,y,Z}可以作为空间的一个基底.同理可知b,c,z和 x,y,a+b+c也不共面,故{b,c,Z}和{x,y,a+b+c} 可以作为空间的基底.因为x=a+b,所以 a,b,x共面,故{a,b,x}不能作为空间的一个 基底
导航 解析: 如图,设 a = 𝐴 𝐵 ,b = 𝐴 𝐴 1 ,c = 𝐴 𝐷 ,则 x = 𝐴 𝐵 1 ,y = 𝐴 𝐷 1 ,z = 𝐴 𝐶 , a+b+c = 𝐴 𝐶 1 .由 A,B1,D1,C 四点不共面可知,向量 x,y,z 不共面, 故{x,y,z}可以作为空间的一个基底.同理可知 b,c,z 和 x,y,a+b+c 也不共面,故{b,c,z}和{x,y,a+b+c} 可以作为空间的基底.因为 x=a+b,所以 a,b,x 共面,故{a,b,x}不能作为空间的一个 基底

导航 二用基底表示空间向量 2.在四面体OABC中,G,H分别为△ABC,△OBC的重心,D为 BC的中点,设0A=a,OB=b,0C=c. (1)试用向量a,b,c表示向量0G和Gi: (2)若E为OA的中点,试用a,b,c表示DE和EG
导航 二 用基底表示空间向量 2.在四面体OABC中,G,H分别为△ABC,△OBC的重心,D为 BC 的中点,设𝑂 𝐴 =a,𝑂 𝐵 =b,𝑂 𝐶 =c. (1)试用向量 a,b,c 表示向量𝑂 𝐺 和𝐺 𝐻 ; (2)若 E 为 OA 的中点,试用 a,b,c 表示𝐷 𝐸 和𝐸 𝐺

导航 解:(1)G为△ABC的重心,D为BC的中点, AG=子AD,0D=0B+0C) ∴.0G=0M+AG=0A+号Ad=0A+号(OD-0A -0A+号×20B+0G)号0A=专(0A+0B+0C)(a+b+c) .H为△OBC的重心,D为BC的中点
导航 解:(1)∵ G为△ABC的重心,D为BC的中点, ∴𝐴 𝐺 = 2 3 𝐴 𝐷 ,𝑂 𝐷 = 1 2 (𝑂 𝐵 + 𝑂 𝐶 ). ∴𝑂 𝐺 = 𝑂 𝐴 + 𝐴 𝐺 = 𝑂 𝐴 + 2 3 𝐴 𝐷 = 𝑂 𝐴 + 2 3 (𝑂 𝐷 − 𝑂 𝐴 ) =𝑂 𝐴 + 2 3 × 1 2 (𝑂 𝐵 + 𝑂 𝐶 )- 2 3 𝑂 𝐴 = 1 3 (𝑂 𝐴 + 𝑂 𝐵 + 𝑂 𝐶 )= 1 3 (a+b+c). ∵H为△OBC的重心,D为BC的中点
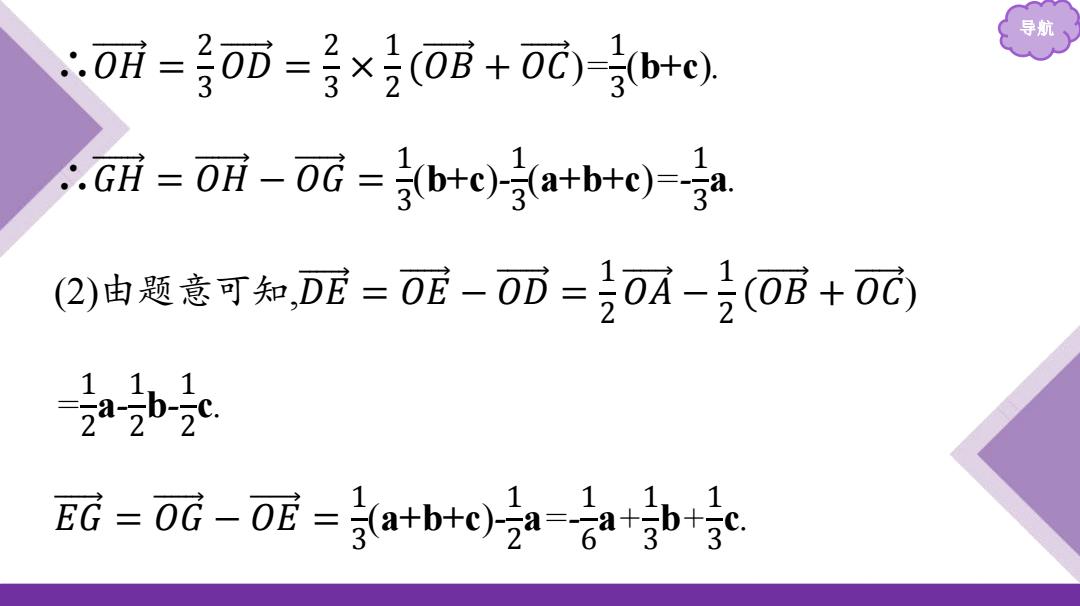
导航 “0丽=号0D=号×0B+0d)b+e以 .GH=OH-OG=(b+e)(a+b+e)-a. 2)由题意可知,D正=0正-0D=0A-20店+0G) =0c-0正=a+b+c)22a+b+c
导航 ∴𝑂 𝐻 = 2 3 𝑂 𝐷 = 2 3 × 1 2 (𝑂 𝐵 + 𝑂 𝐶 )= 1 3 (b+c). ∴𝐺 𝐻 = 𝑂 𝐻 − 𝑂 𝐺 = 1 3 (b+c)- 1 3 (a+b+c)=- 1 3 a. (2)由题意可知,𝐷 𝐸 = 𝑂 𝐸 − 𝑂 𝐷 = 1 2 𝑂 𝐴 − 1 2 (𝑂 𝐵 + 𝑂 𝐶 ) = 1 2 a- 1 2 b- 1 2 c. 𝐸 𝐺 = 𝑂 𝐺 − 𝑂 𝐸 = 1 3 (a+b+c)- 1 2 a=- 1 6 a+ 1 3 b+ 1 3 c