
O#A定积分的换元积分法求定积分Vsinx-sinxdx.解因为/sinx-sinx=Vsinxcosx=cosx|/sinx,在[0,]上,|cosx=cosx;在「,元]上,|cosx=-cosx.于是Vsin x- sin'xdx=lcosx/Vsin xdx=Vsin xdsinx-Vsin xdsinx232322242sin2sin211X3333372
定积分的换元积分法 6 例 2 解

O定积分的换元积分法结论1设函数y=f(x)在区间[-a,a](a>0)上连续,试证:(1 b, f(x)dx = Lf(x)+ f(- x)]dx0,f(x)是奇函数(2 b. f(x)dx =2.f(x)dx,f(x)是偶函数
定积分的换元积分法 7 结论1

OAA定积分的换元积分法结论1设函数y= f(x)在区间[-a,α](α>0)上连续,试证:(1 6, f(x)dx = Lf(x)+ f(- x)]dx0,f(x)是奇函数,(2 6 f(x)dx =)20 f(x)dx,f(x)是偶函数D证(1)因为函数y=f(x)在[-a,a]上连续,所以f(x)dx存在,由定积分积分区间的可加性得. f(x)dx=0. f(x)dx+f(x)dx,对上式中的of(x)dx,设x=-t,则dx=-dt,且当x=-α时,t=a;当x=0时,t=0.于是O. f(x)dx =-O F(-0)dt = f(-1)d = f(-x)dx,所以. f(x)dx =[f(x)- f(x)]dx.8
定积分的换元积分法 8 证 结论1
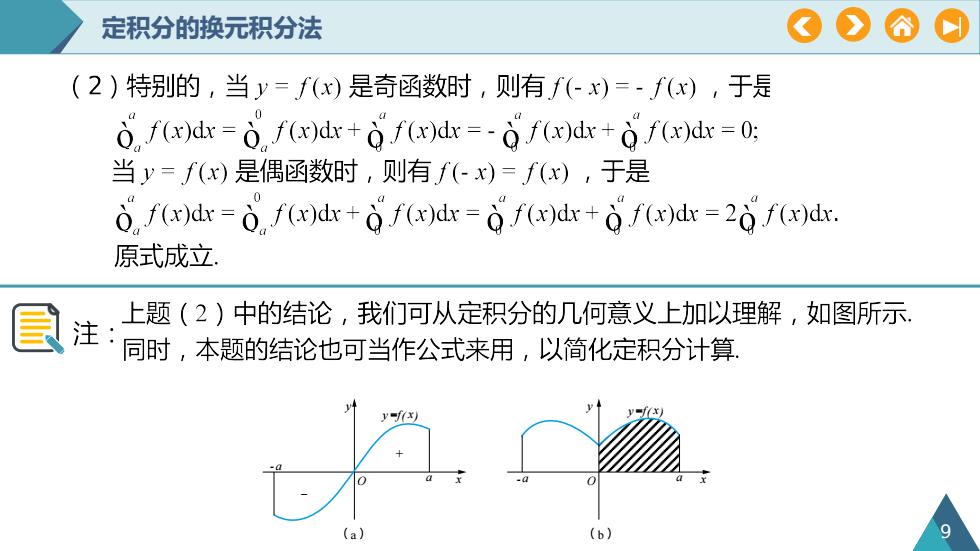
P定积分的换元积分法(2)特别的,当y=f(x)是奇函数时,则有f(-x))=-f(x),于是0 f(x)dx = 0, f(x)dx + f(x)dx = - f(x)dx + f(x)dx = 0;当y=f(x)是偶函数时,则有f(-x)=f(x),于是O, f(x)dx = 0. f(x)dx + 0 f(x)dx = f(x)dx + 0 f(x)dx = 20 f(x)dx.原式成立上题(2)中的结论,我们可从定积分的几何意义上加以理解,如图所示注同时,本题的结论也可当作公式来用,以简化定积分计算(a)(b)
定积分的换元积分法 9 y=f( x) y y O a x O x y=f( x) + - a - a - a (a) (b)