
Pk△kC(s)梅逊公式介绍R-C△R(s)称为系统特征式△= 1- ZLa + L,Lc -ZLdLeL+..其中:所有单独回路增益之和ZLaLL一所有两两互不接触回路增益乘积之和LdLL一所有三个互不接触回路增益乘积之和Pk一从R(s)到C(s)的第k条前向通路传递函数△称为第条前向通路的余子式△求法:去掉第条前向通路后所求的△△Ak=1-ELA+ ZLbLc- ZLdLeLF+
11 Pk—从R(s)到C(s)的第k条前向通路传递函数 梅逊公式介绍 R-C C(s) R(s) = ∑Pk△k △ : △称为系统特征式 △= 其中: —∑La 所有单独回路增益之和 ∑LbLc—所有两两互不接触回路增益乘积之和 ∑LdLeLf—所有三个互不接触回路增益乘积之和 △k称为第k条前向通路的余子式 △k求法: 去掉第k条前向通路后所求的△ - ∑La + ∑LbLc 1 -∑LdLeLf+. △k=1-∑LA+ ∑LBLC- ∑LDLELF+
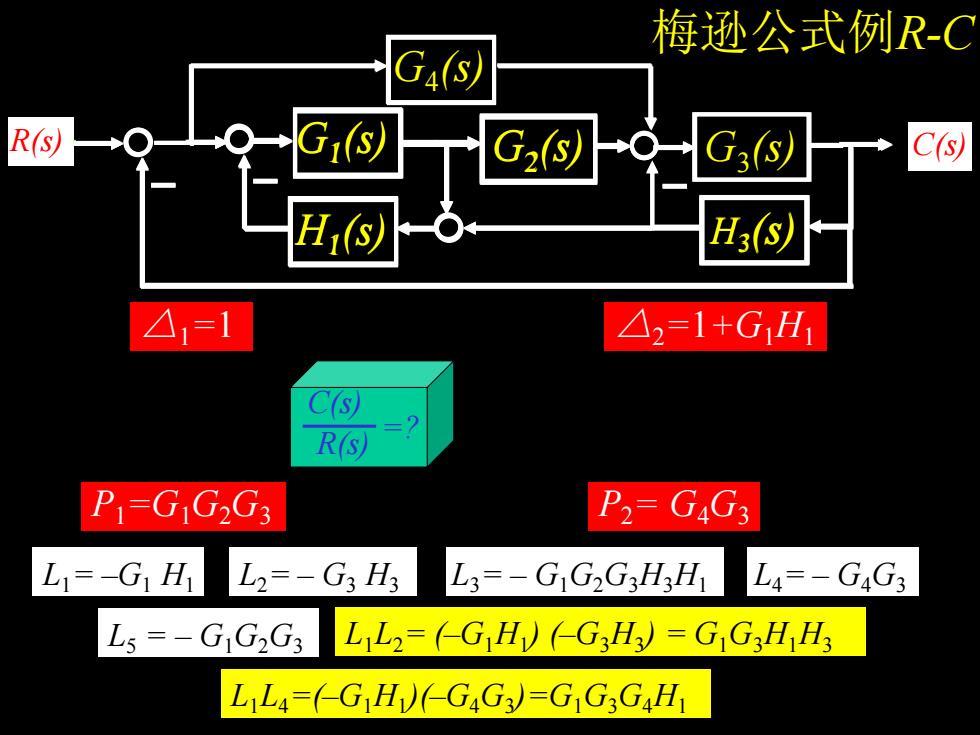
梅逊公式例R-CG4(s)Gi(s)R(s)C(s)G3(s)G2(s)YTH;(s)H3(s)△,=1△2=1+G,HC(s)2R(s)P1=G,G2G3P2= G4G3L,=-G HL2=- G3 H3L,=-G,G,G,H,HL4=- G4G3L,L2= (-G,H) (-G,H) = G,G,H,H3Ls = - G,G,G3L,L4=(-G,H)(-G4G3)=G,G,G4H
12 R(s) C(s) L1= –G1 H1 L2= – G3 H3 L3= – G1G2G3H3H1 L4= – G4G3 L5 = – G1G2G3 L1L2= (–G1H1 ) (–G3H3 ) = G1G3H1H3 L1L4=(–G1H1 )(–G4G3 )=G1G3G4H1 G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) H3 (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G1 (s) G2 (s) G3 G1 (s) (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) G4 (s) G3 (s) 梅逊公式例R-C H1 (s) H3 (s) G1 (s) G2 (s) G4 (s) H1 (s) H3 (s) G1 (s) G2 (s) G3 (s) P1=G1G2G3 P2= G4G3 △1=1 △2=1+G1H1 C(s) R(s) =? 请你写出答案,行吗?
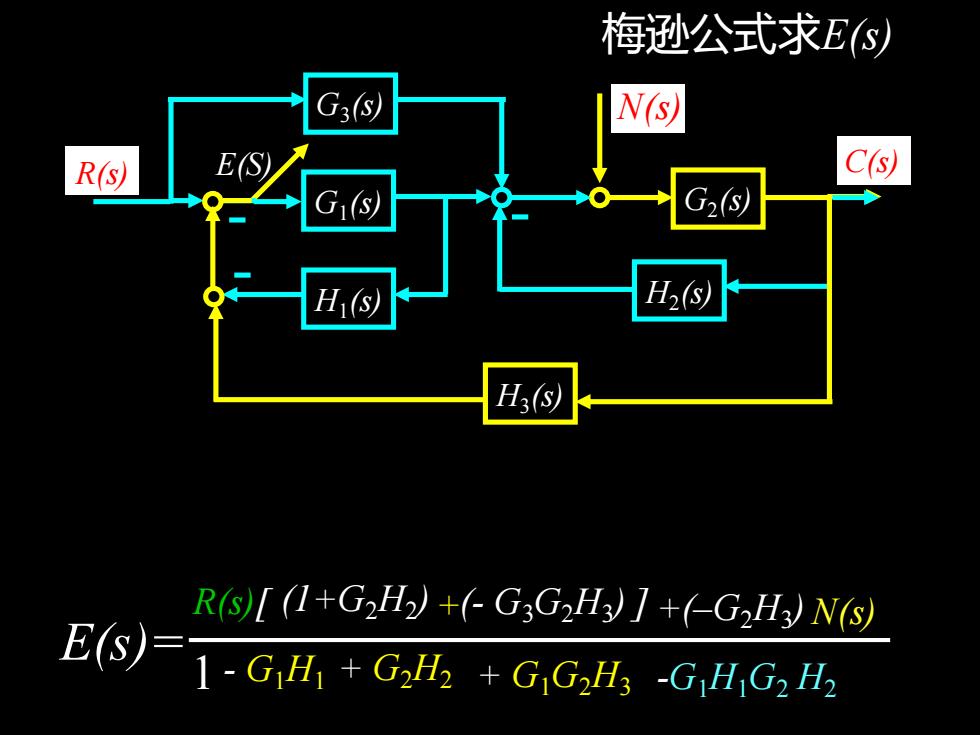
梅逊公式求E(S)N(s)G3(S)SE(S)R(s)Gi(s)G2(s)H2(s)Hi(s)H3 (s)R(s)[ (1+G2H2) +(- G3G2H3) / +(-G2H3) N(s)E(s):1 - G,H1 +G,H2 + G,G2H3-G,H,G2 H2
13 G1 (s) G3 (s) H1 (s) G2 (s) H3 (s) H2 (s) R(s) C(s) N(s) E(S) G1 (s) G3 (s) H1 (s) G2 (s) H3 (s) H2 (s) R(s) C(s) N(s) E(S) P1=1 △1=1+G2H2 P1△1= ? E(s)=1 + G2H2 + G1G2H3 -G1H1G2 H2 - G1H1 (–G2H3 R(s)[ ] ) N(s) (1+G2H2 ) (- G3G2H3 + ) + R(s) E(S) G1 (s) G3 (s) H1 (s) G2 (s) H3 (s) H2 (s) C(s) N(s) R(s) E(S) G3 (s) G2 (s) H3 (s) R(s) E(S) G1 (s) H1 (s) H2 (s) C(s) P2= - G3G2H3 △2= 1 P2△2=? 梅逊公式求E(s) P1= –G2H3 △1= 1 N(s) G1 (s) H1 (s) H2 (s) C(s) G3 (s) G2 (s) H3 (s) R(s) E(S)
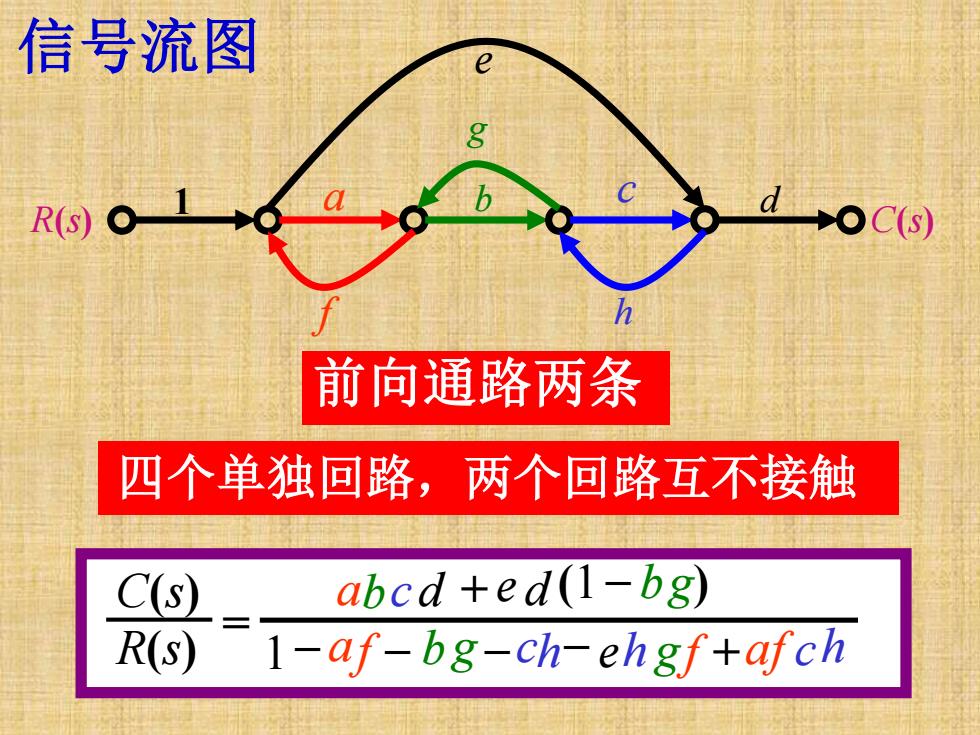
信号流图gbaVOC(SR(S)h前向通路两条四个单独回路,两个回路互不接触abcd +ed(l-bg)C(s)R(s)1-af-bg-ch-ehgf+afch
14 四个单独回路,两个回路互不接触 e 1 a b c d f g h R(s) C(s) C(s) R(s) = 1 – – – – + + 前向通路两条 信号流图 af b g ch eh gf af ch abc d e d (1 – bg)

第三章线性系统的时域分析法3-1 时域性能指标3-2一阶系统时域分析3-3二阶系统时域分析3-4稳定性分析3-6稳态误差计算
15 第三章 线性系统的时域分析法 3-1 时域性能指标 3-2 一阶系统时域分析 3-3 二阶系统时域分析 3-4 稳定性分析 3-6 稳态误差计算