
第5章线性系统的频域分析法Frequency-response analysis5.1频率特性及其表示法幅相曲线对数频率特性曲线5.2典型环节的幅相曲线5.3稳定裕度和判据已经学习了用线性常微分方程和传递函数描述线性定常系统,这两种模型分别在时域和复频域中对系统进行了描述。下面介绍一种数学模型一频率特性函数,这种模型是对系统的一种频域刻画,在系统分析中有重要作用。①判断系统是否稳定,②稳定程度一一稳定裕度。应用频率特性研究线性系统的经典方法称为频域分析法。(是以传递函数为基础的又一种图解法。与根轨迹法相比较,根轨迹法是一种非常实用的求取闭环特征方程式根的图解法,特别对于高阶系统)与其他方法相比较,频率响应法还具有如下特点:(1)频率特性具有明确的物理意义,它可以用实验的方法来确定,这对于难以列写微分方程式的元部件或系统来说,具有重要的实际意义。(2)由于频率响应法主要通过开环频率特性的图形对系统进行分析,97
97 第 5 章 线性系统的频域分析法 Frequency-response analysis 5.1 频率特性及其表示法 幅相曲线 对数频率特性曲线 5.2 典型环节的幅相曲线 5.3 稳定裕度和判据 已经学习了用线性常微分方程和传递函数描述线性定常系统,这两种 模型分别在时域和复频域中对系统进行了描述。下面介绍一种数学模型— —频率特性函数,这种模型是对系统的一种频域刻画,在系统分析中有重 要作用。判断系统是否稳定,稳定程度——稳定裕度。 应用频率特性研究线性系统的经典方法称为频域分析法。(是以传递函 数为基础的又一种图解法。与根轨迹法相比较,根轨迹法是一种非常实用 的求取闭环特征方程式根的图解法,特别对于高阶系统)。 与其他方法相比较,频率响应法还具有如下特点: (1)频率特性具有明确的物理意义,它可以用实验的方法来确定,这 对于难以列写微分方程式的元部件或系统来说,具有重要的实际意义。 (2)由于频率响应法主要通过开环频率特性的图形对系统进行分析

因而具有形象直观和计算量少的特点。(3)频率响应法不仅适用于线性定常系统,而且还适用于传递函数不是有理数的纯滞后系统和部分非线性系统的分析。5.1频率特性及其表示法5.1.1频率特性的基本概念频率特性又称频率响应,它是系统(或元件)对不同频率正弦输入信号的响应特性。设线性系统的输入为一频率为的正弦信号,在稳态时,系统的输出具有和输入同频率的正弦函数,但其振幅和相位一般均不同于输入量,且随着输入信号频率的变化而变化,如图5.1所示。线性系统图98
98 因而具有形象直观和计算量少的特点。 (3)频率响应法不仅适用于线性定常系统,而且还适用于传递函数不 是有理数的纯滞后系统和部分非线性系统的分析。 5.1 频率特性及其表示法 5.1.1 频率特性的基本概念 频率特性又称频率响应,它是系统(或元件)对不同频率正弦输入信号的 响应特性。设线性系统的输入为一频率为的正弦信号,在稳态时,系统的 输出具有和输入同频率的正弦函数,但其振幅和相位一般均不同于输入量, 且随着输入信号频率的变化而变化,如图 5.1 所示。 0 0.5 1 1.5 2 2.5 3 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 线 性 系 统 0 0.5 1 1.5 2 2.5 3 -5 -4 -3 -2 -1 0 1 2 3 4 5 图
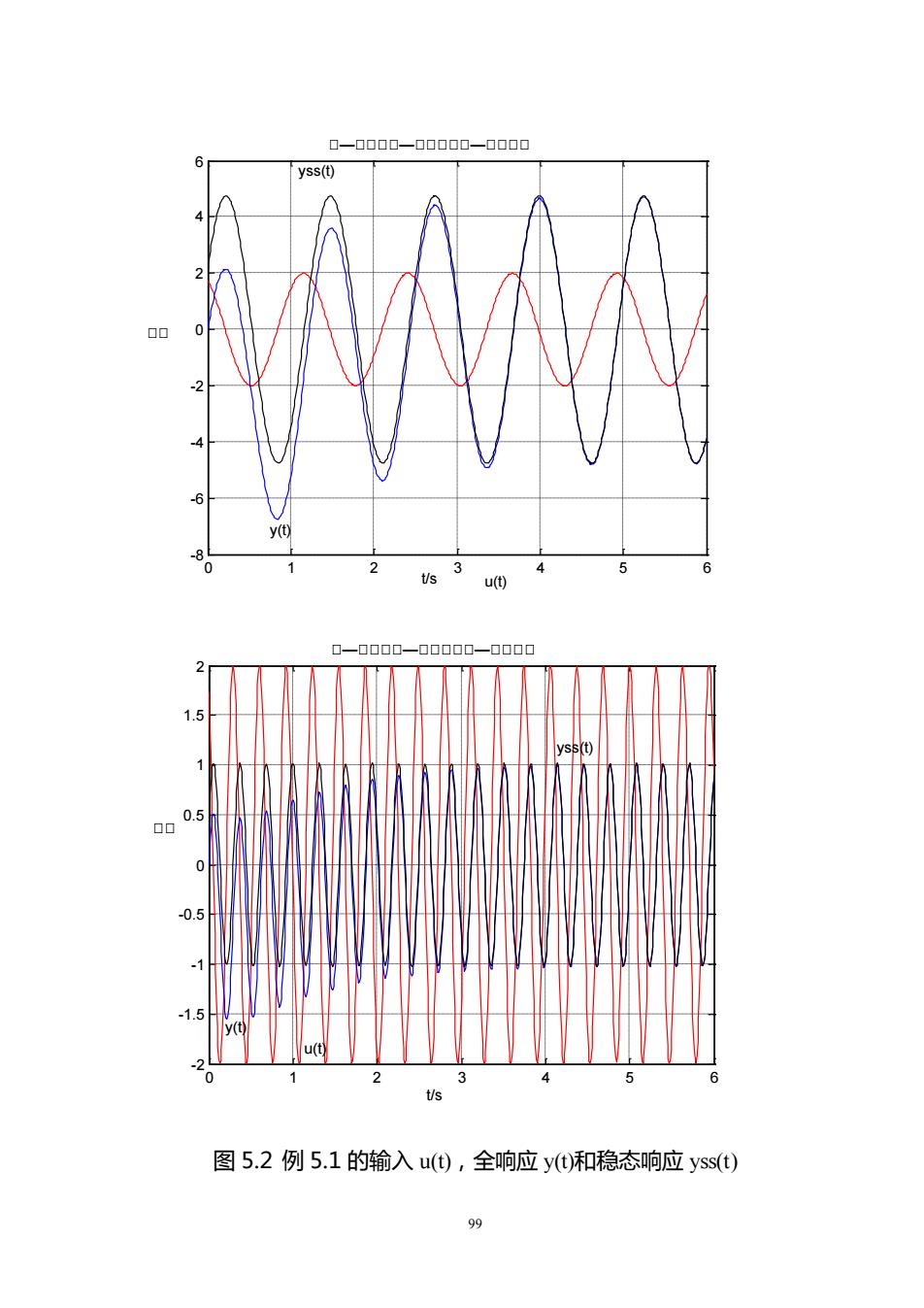
00000000000000Cyss(t)吕-2-4-6Vy(t)-82356014t/su(t)口口口0口-口口口口-1.5yss(t)0.5吕00.5-1-1.5U123456t/s图5.2例5.1的输入u(t),全响应y(t)和稳态响应yss(t)99
99 0 1 2 3 4 5 6 -8 -6 -4 -2 0 2 4 6 t/s 幅幅 u(t) y(t) yss(t) 幅—幅幅幅幅—幅幅幅幅幅—幅幅幅幅 0 1 2 3 4 5 6 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 t/s 幅幅 u(t) y(t) yss(t) 幅—幅幅幅幅—幅幅幅幅幅—幅幅幅幅 图 5.2 例 5.1 的输入 u(t),全响应 y(t)和稳态响应 yss(t)

10s +50考虑系统传递函数为G(s)=s2 +4s+3u(t)=2cos(5t+30°)u(t) = 2cos(20t + 300)设系统的传递函数为 C%=G(s)=U)V(s)R(s)Ao已知输入r(t)=Asin(ot),其拉氏变换R(s)=4,A 为常量,则系统输出U(s)Ao为C(s) = G(s)R(s)= V(s) s2 +02U(s)Ao(5-1)(s$+ p:)(s+ p2).(s+ pn) ? +02式中,-Pl-P2…-p,为G(s)的极点。对于稳定系统,这些极点都位于s平面的左方,即它们的实部均为负值。为简单起见,令G(s)的极点均为相异的实数极点,则式(5-1)改写为C(s)=_baa(5-2)?s+pis+jos-joa,a和b,(i=1,2,n)均为待定系数。对上式取拉氏反变换,求得c(t)= ae-jot +e jan +b,e-P)(5-3)i=1当t→时,系统响应的瞬态分量be-pt趋向于零,其稳态分量为i=lc(t)= ae-jon +aejor(5-4)其中系数由下式确定AoAo()+jo)=G()a=G(s)-+a2($+ jo)l2100
100 考虑系统传递函数为 4 3 10 50 ( ) 2 + + + = s s s G s u(t) = 2cos(5t + 30) u(t) = 2cos(20t + 30) 设系统的传递函数为 ( ) ( ) ( ) ( ) ( ) V s U s G s R s C s = = 已知输入 r(t) = Asin(t) ,其拉氏变换 2 2 ( ) + = s A R s ,A 为常量,则系统输出 为 2 2 ( ) ( ) ( ) ( ) ( ) + = = s A V s U s C s G s R s 2 2 1 2 ( )( ) ( ) ( ) + + + + = s A s p s p s p U s n (5-1) 式中,− p −p − pn , , 1 2 为 G(s)的极点。对于稳定系统,这些极点都位于 s 平 面的左方,即它们的实部均为负值。为简单起见,令 G(s)的极点均为相异 的实数极点,则式(5-1) 改写为 s j a s j a s p b C s n i i i − + + + + = =1 ( ) (5-2) a,a b (i 1,2, n) 和 i = 均为待定系数。对上式取拉氏反变换,求得 = − − = + + n i p t i j t j t i c t ae ae b e 1 ( ) (5-3) 当 t → 时,系统响应的瞬态分量 = − n i p t i i b e 1 趋向于零,其稳态分量为 j t j t t c t ae ae = + − → ( ) (5-4) 其中系数由下式确定 j A s j G j s j s j A s j G j s A a G s s j s j 2 ( ) ( ) ( )( ) ( ) ( ) ( ) 2 2 − + = − + − + = − + = =− =− (5-5)

AoAoA(5-6)a=G(s)? +@2(s- jo)=G(jo)=G(j@)(s-jo))(s+ jo)(s- jo)(s21由于G(jo)是一个复数向量,因而可表示为Gja) = a()+ jb) = G(jo)e km= A(0)ej(o)(5-7)c(0)+ jd(0)因为G(s)的分子和分母多项式为实系数,故a(の)和c(の)为关于的偶次幂实系数多项式,b(の)和d(の)为关于の的奇次幂实系数多项式,即a(の)和c()为の的偶函数,b(の)和d(の)为の的奇函数。(jo)4 = @4(jo)"= jo(jo)?=-o?(jo)3 =-j03(5-8)In = 0,2,4,...j02n+1[n=0,2,4,...2n(jo)2n+lGjo)2n-jo2n+1[n= 1,3,5,..n= 1,3,5,..a?(0) +b (0)(5-9)JG(jo)] =Nc(0)+d?(0)b(の)d(o)(5-10)-argig/GUa) arg g (c(の)G(-j 0) = a(0) jb -I (j0)e km= A(0)e-jg(α)(5-11)c(o)- jd(o)[A(0) =|G(jo)]/ G(ja)(5-12)[(0)= /G(ja)将式(5-5)、式(5-6)、式(5-7)和式(5-11)代入式(5-4),求得c()=e +e= A(0)e-()+A()e)=A(0)si(+()2j2j(5-13)以上证明了线性系统的稳态输出是和输入具有相同频率的正弦信号,101
101 j A s j G j s j s j A s j G j s A a G s s j s j 2 ( ) ( ) ( )( ) ( ) ( ) ( ) 2 2 − = + − − = + = = = (5-6) 由于 G( j) 是一个复数向量,因而可表示为 ( ) ( ) ( ) ( ) ( ) ( ) ( ) G j j G j e c jd a jb G j = + + = ( ) ( ) j = A e (5-7) 因为 G(s)的分子和分母多项式为实系数 ,故 a()和c() 为关于 的偶次幂实 系数多项式, b()和d() 为关于 的奇次幂实系数多项式,即 a()和c() 为 的偶函数, b()和d() 为 的奇函数。 = = − = = = − = = = − = − = + + + 1,3,5, 0,2,4, ( ) 1,3,5, 0,2,4, ( ) ( ) ( ) ( ) ( ) 2 2 2 2 1 2 1 2 1 1 2 2 3 3 4 4 n n j n n j j j j j j j j j n n n n n n (5-8) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 c d a b G j + + = (5-9) ( ) ( ) arg ( ) ( ) arg ( ) c d tg a b tg G j = − (5-10) ( ) ( ) ( ) ( ) ( ) ( ) ( ) G j j G j e c jd a jb G j − = − − − = ( ) ( ) j A e − = (5-11) = = ( ) ( ) ( ) ( ) G j A G j G( j) (5-12) 将式(5-5) 、式(5-6)、 式(5-7)和 式(5-11)代入式 (5-4),求得 ( ) sin( ( )) 2 ( ) 2 ( ) ( ) ( ) ( ) + = + − = + = − − − A A t j A A e e j A c t ae ae A e e j t j t j j t j j t (5-13) 以上证明了线性系统的稳态输出是和输入具有相同频率的正弦信号