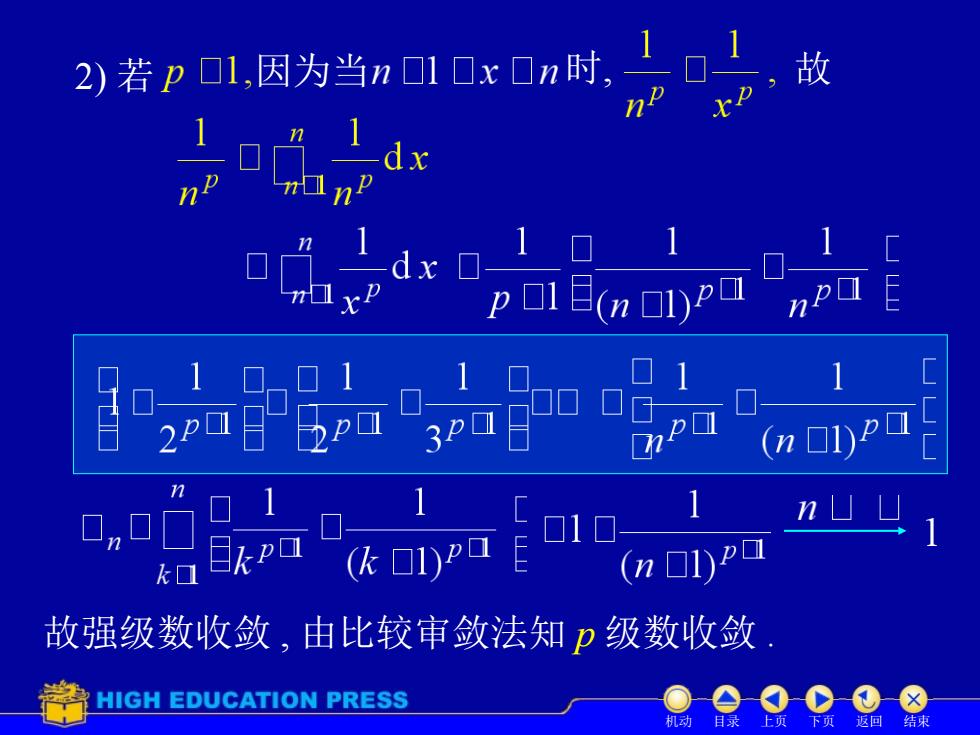
故2)若pl,因为当nlxn时XPopLnnn口口n11目kp(k 口1)p(n1)pk口故强级数收敛,由比较审敛法知p级数收敛HIGH EDUCATION PRESS下页返回机动自录上贝结束
因为当 故 考虑强级数 的部分和 故强级数收敛 , 由比较审敛法知 p 级数收敛 . 2) 若 时, 机动 目录 上页 下页 返回 结束

调和级数与p级数是两个常用的比较级数若存在NZ,对一切nN,则un发散;U7n口1),则收敛nJ口unnHIGHEDUCATION PRESS机动目录下页返回上贝结束
调和级数与 p 级数是两个常用的比较级数. 若存在 对一切 机动 目录 上页 下页 返回 结束

1发散例2.证明级数n(n l)n1证:因为(n口1,2,口)n(nln l□1)n福发散而级数knnk 2根据比较审敛法可知,所给级数发散HIGH EDUCATION PRESS目录下页返回机动上贝结束
证明级数 发散 . 证: 因为 而级数 发散 根据比较审敛法可知, 所给级数发散 . 例2. 机动 目录 上页 下页 返回 结束

设两正项级数定理3.(比较审敛法的极限形式)unlun,vn满足lim 口l, 则有nVnnn(1)当0<l<o 时,两个级数同时收敛或发散:口也收敛;un(2)当l=0 且vn收敛时,nn口口(3)当 / =o 且vn发散时, un 也发散,nn证:据极限定义,对O,存在NZ,当nN时nC(1)HIGHEDUCATION PRESS目录下页返回机动上贝结束
定理3. (比较审敛法的极限形式) 则有 两个级数同时收敛或发散 ; (2) 当 l = 0 (3) 当 l =∞ 证: 据极限定义, 设两正项级数 满足 (1) 当 0 < l <∞ 时, 机动 目录 上页 下页 返回 结束

(n N)(1 )yn un (1 )Vn口口un与Vn(1)当0<l<o时,取l,由定理2 可知nn同时收敛或同时发散:(2)当l= O时,利用 un (l )vn(n N),由定理2 知口若vn收敛,则un 也收敛;nnUn(3)当l=时,存在NZ,当nN时□1,即vunn口由定理2可知,若■vn发散,则un也发散nnHIGH EDUCATION PRESS目录上页下页返回机动结束
由定理 2 可知 同时收敛或同时发散 ; (3) 当l = ∞时, 即 由定理2可知, 若 发散 , (1) 当0 < l <∞时, (2) 当l = 0时, 由定理2 知 若 收敛 , 机动 目录 上页 下页 返回 结束