
矢量场的通量与散度 曲面正向 ·将曲面的一个面元用矢量S来表示,其方向取为面元 的法线方向,其大小为S,即 dS nds ·n是面元法线方向的单位矢量。 ■开曲面:设这个开曲面是由封闭曲线所围成的,则选定绕行1 的方向后,沿绕行方向按右手螺旋的拇指方向就是的方向 ■闭曲面:外侧为n的方向 lexu@mail.xidian.edu.cn
矢量场的通量与散度 曲面正向 • 将曲面的一个面元用矢量dS来表示,其方向取为面元 的法线方向, 其大小为dS ,即 dS nds ˆ • n是面元法线方向的单位矢量。 开曲面 设这个开曲面是由封闭曲线 l所围成的 则选定绕行 l dS nds 开曲面:设这个开曲面是由封闭曲线 l所围成的,则选定绕行 l 的方向后,沿绕行方向按右手螺旋的拇指方向就是 n的方向 闭曲面:外侧为 n的方向 lexu@mail.xidian.edu.cn 11

矢量场的通量与散度 ■通量 ·将曲面S各面元上的A相加,它表示矢量场A穿过整 个曲面S的通量,也称为矢量A在曲面S上的面积分 ·设AM为一矢量场,沿其中有向曲面S正(负)侧曲面 积分称为矢量场AM)向s正(负)侧穿过曲面S的通量。 ■如果曲面是一个开曲面,则 w=小AS=∫- 。如果曲面是一个闭曲面,则 w=A西 lexu@mail.xidian.edu.cn 12
矢量场的通量与散度 通 量 • 将曲面 S各面元上的A·ds相加,它表示矢量场 A穿过整 个曲面 S的通量,也称为矢量A在曲面 S上的面积分 • 设A (M)为一矢量场,沿其中有向曲面 S 正 ( 负 )侧曲面 积分称为矢量场 积分称为矢量场 A (M) 向 s 正 ( 负 )侧穿过曲面 S 的通量 。 如果曲面是一个开曲面,则 A dS A dS ˆ 如果曲面是一个闭曲面,则 S S A dS A ndS S A dS lexu@mail.xidian.edu.cn 12 S
矢量场的通量与散度 。Note1:通量可以叠加: A=4 Φ=2w.=2川a ·Note2:直角坐标系中: A=P(x,a+Qx+R(x业国 S=山d止R+dh+山鸡 D= A5=Pdt+Qd在+Rbd lexu@mail.xidian.edu.cn
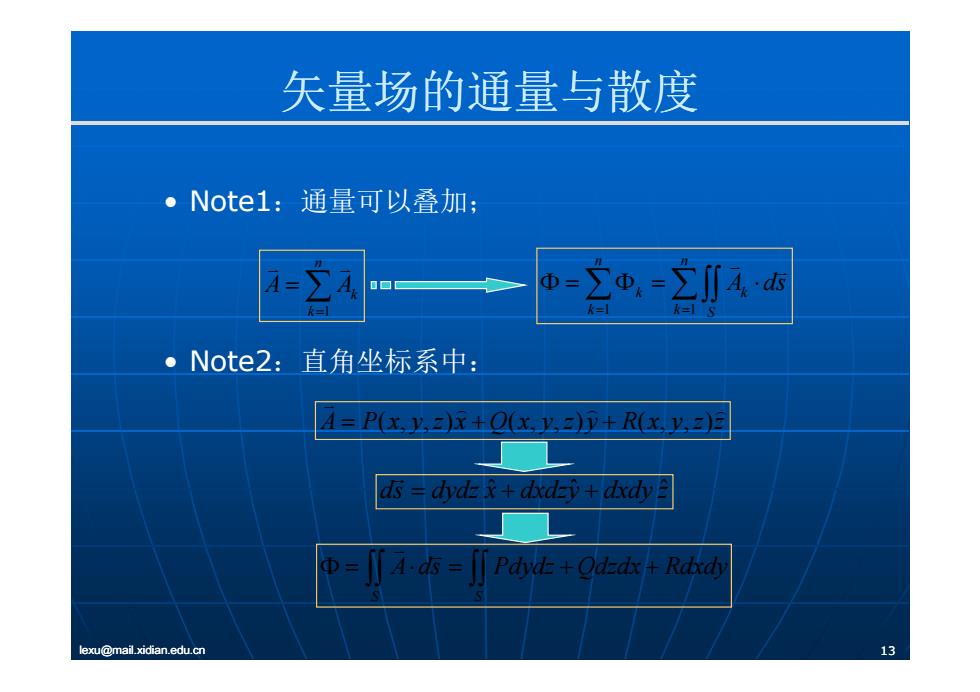
矢量场的通量与散度 • Note1:通量 以叠加 可 ; n n n 1 k k A A 1 1 k k k k S A ds • Note2:直角坐标系中: A Pxyzx Qxyzy Rxyzz ( )( )( ) A Pxyzx Qxyzy Rxyzz ( , , ) ( , , ) ( , , ) ds d ydz x dxdz ˆ ˆ y dxdy zˆ A ds Pdydz Qdzdx Rdxdy y yy lexu@mail.xidian.edu.cn 13 S S

矢量场的通量与散度 ■物理意义 ·开曲面 ■当Q>0:流向正侧流量多于流向负侧流量: ■当Q<0:流向正侧流量少于流向负侧流量: ·当Q=0:流向正侧流量等于流向负侧流量。 。闭曲面 ■当Q>0:穿出的通量大于穿入的通量,有正源: ■当Q<0:穿出的通量小于穿入的通量,有负源: ■当Q=0:穿出的通量等于穿入的通量,正、负源抵消或无源。 lexu@mail.xidian.edu.cn 14
矢量场的通量与散度 物 意义 理 • 开曲面 当Q>0:流向正侧流量多于流向负侧流量; 当 Q 0: < 流向正侧流量少于流向负侧流量; 当Q=0:流向正侧流量等于流向负侧流量。 • 闭曲面 当Q>0:穿出的通量大于穿入的通量,有正源; 当Q<0:穿出的通量小于穿入的通量,有负源; 当Q=0:穿出的通量等于穿入的通量,正、负源抵消或无源。 lexu@mail.xidian.edu.cn 14

矢量场的通量与散度 矢量场:下=xi+yj+2 ■例1己知 曲 面:x2+y2=2与=围成闭曲面 求穿出S 的通量。 [解] =川产述 产+行-西S上失径与面元垂直 81 F,d=川dh止+k止+dhd S2 =Hh=Hdhd=H=πH lexu@mail.xidian.edu.cn 15
矢量场的通量与散度 :r xi y j zk 矢 量 场 例1 已知 求穿出 S 的通量 。 矢 量 场:r xi y j zk 222 曲 面 与 围成闭曲面 : x y z zH 的通量 。 [ 解 ] (S ) s r ds d d 上 矢 径 与 面 元 垂 直 1 2 2 (S ) s s r ds r ds r ds xdydz ydxdz zdxdy 上 矢 径 与 面 元 垂 直 1 1 2 3 s s r ds xdydz ydxdz zdxdy Hdxdy H dxdy HH H lexu@mail.xidian.edu.cn 15 1 1 y y